4.5. Механизмы для преобразования вращательного движения

В машинном агрегате (рис. 69), как правило, могут быть выделены три основные части: двигатель; привод, снижающий достаточно большое число оборотов стандартных электродвигателей до необходимого технологического значения; исполнительный механизм. Привод и представляет собой механизм для преобразования враща­тельного движения вокруг одной оси во вращательное движение вокруг другой.

Рис. 69

Наиболее часто в качестве привода используется зубчатый ме­ханизм в различных модификациях.

Цилиндрические зубчатые колеса с прямыми зубцами. Как уже было отмечено, зубчатый механизм или так называемая зуб­чатая передача служит для преобразования вращательного движения с угловой частотой (скоростью) ω₁ (или числом оборотов в мину­ту n₁) во вращательное движение с угловой частотой ω₂ (или числом оборотов в минуту n₂). Отношение угловых частот ω₁ и ω₂ называется передаточным отношением, т.е.

.

Цилиндрические зубчатые колеса представляют собой диски, толщиной в, на ободе которых нарезаны зубья (рис. 70).

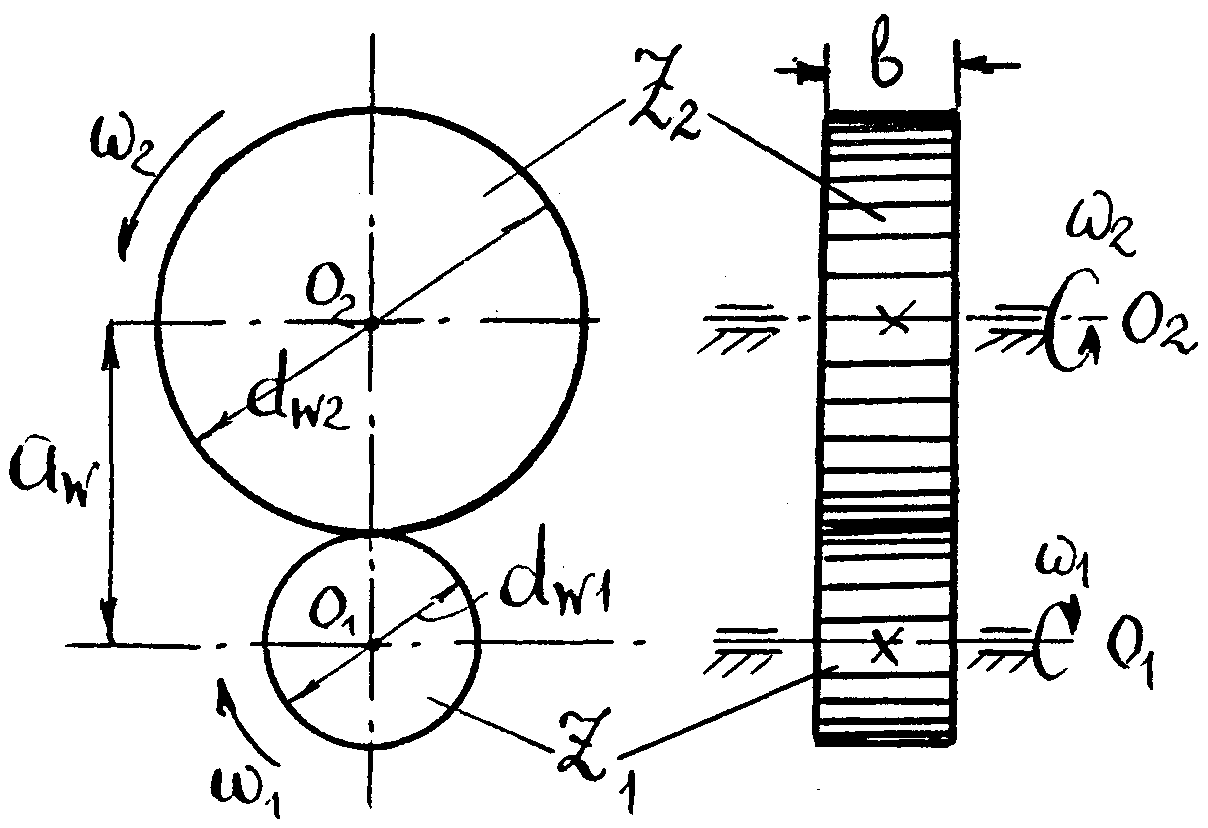
Рис. 70

Цилиндрические зубчатые колеса с прямыми зубцами (зубцы располо­жены параллельно оси вала) применяются для передачи движения между параллельными валами. Целый ряд требований технологического, эксплуатационного и др. характера привели к использованию, в ос­новном, эвольвентного профиля зубцов. Основное требование, предъявляемое зубчатым передачам, - это постоянство передаточного отношения. Этому условию удовлетворяют так называемые взаимоогибаемые кривые, описывающие профиль зуба, общая нормаль к которым в точке их касания проходит через полюс зацепления Р, не меняющий своего положения на линии центров О₁О₂. Этому условию удовлетворяют и эвольвенты круга, удобные с технологической точки зрения. Общая нормаль к этом кривым NN не меняет своего положения в пространстве в процессе их перекатывания и является линией закрепления, т.е. геометрическим местом точек касания сопряженных профилей. Таким образом, основная теорема закрепления может быть сформулирована так: общая нормаль к профилям зубцов NN, проведенная в точке их касания, делит линию центров О₁О₂ на части, обратно пропорциональные угловым скоростям колес. В специальных случаях ис­пользуются и некоторые другие формы профилей зубьев.

Пусть имеем два зубчатых колеса с числами зубцов z₁ и z₂ (рис. 71). Основной кинематической характеристикой зубчатого колеса является диаметр на­чальной (делительной) окружности d_w. Началь­ные окружности сопря­женных колес перека­тываются друг по дру­гу бeз скольжения. Ду­га аb называется шагом зубчатого ко­леса. Очевидно,

и , .

Величина m называется модулем передачи. Модуль остирован, измеряется в мм. Очевидно, для двух соп­ряженных колес модуль и шаг должны быть одинаковы.

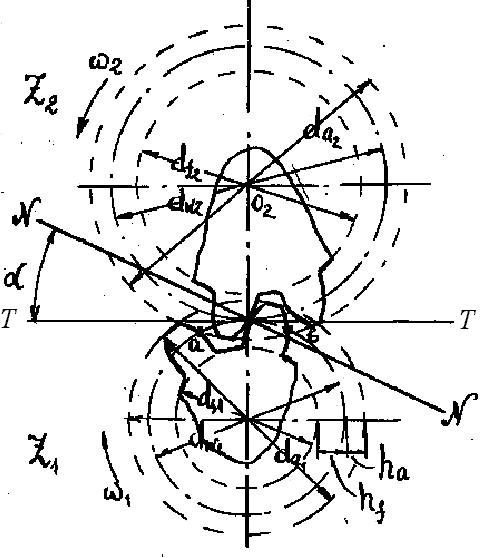
Рис. 71

Тогда,

.

Передаточное число зубчатой пары выразится как

.

Высота зуба , где h_a – высота головки зуба, h_f – высота ножки зуба. В нормальных зубчатых колесах h_a=m и h_f=1,2m. Тогда диаметры окружностей головок d_a будут

,

и диаметры окружностей ножек d_f (впадин)

.

Давление профиля зуба ведущего колеса на профиль зуба ведомого передается по нормали к профилям в точке их контакта. Этой нормалью является (по построению профиля зуба) прямая NN, проходящая под углом α к линии TT, касательной к начальным окружностям d_w1 и d_w2. Угол α называется углом зацепления и принят в большинстве колес равным 20°. Линия NN нормальна к профилям зубцов в точке их контак­та и называется линией зацепления, являясь геометрическим местом точек касаний сопряженных профилей.

Серия зубчатых колес. Передаточное отношение (число) в одной паре колес редко делается больше 5–6. С целью увели­чения передаточного отношения применяют серию зубчатых колес (рис. 72).

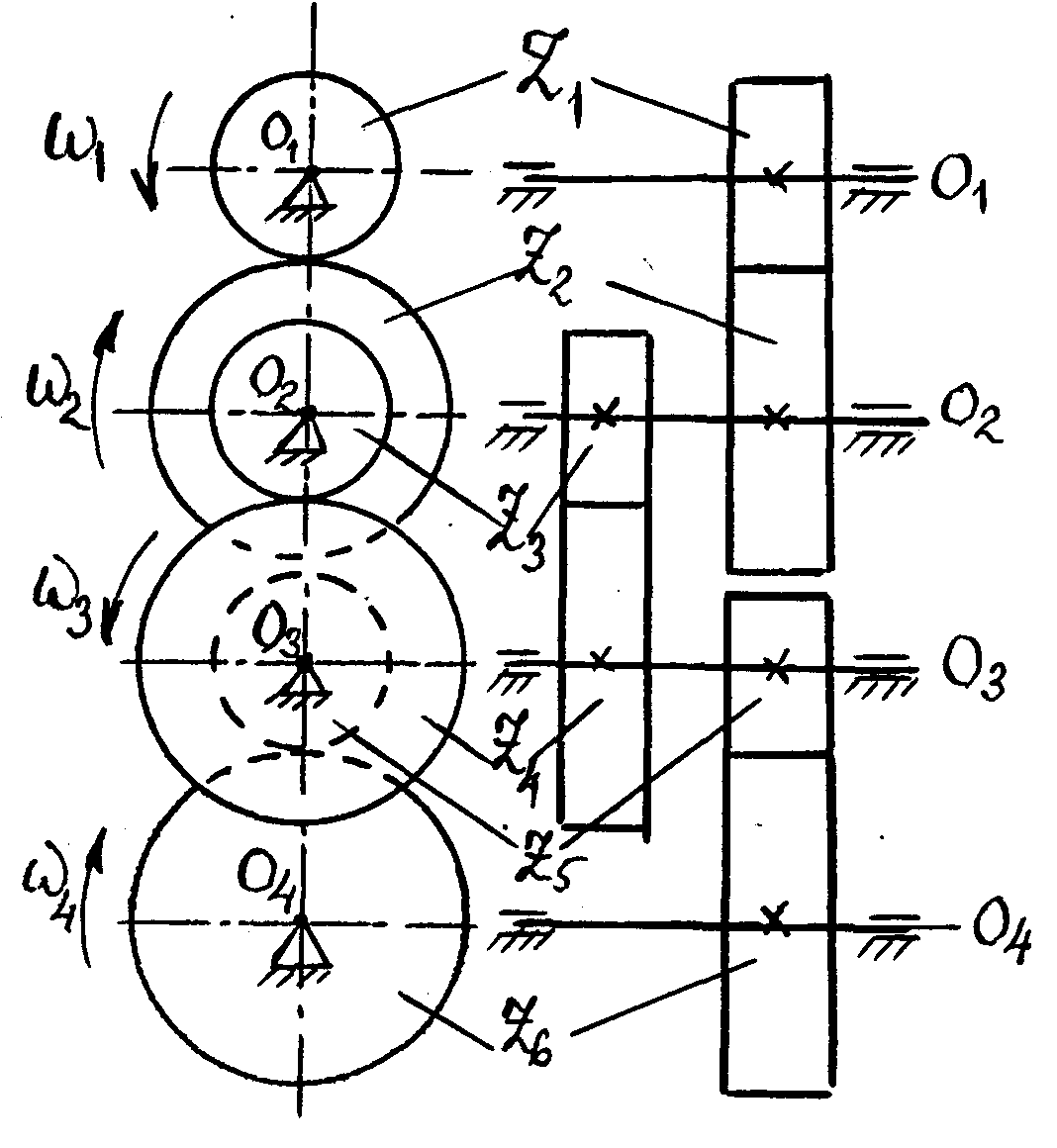
Рис. 72

Передаточные отношения каждой пары колес будут (знак «-» опущен)

; ; .

Перемножая их, получим . Но .

Поэтому или через числа зубцов , где k – число внешних зацеплений.

Передача цилиндрическими колесами с косыми зубьями. Такие передачи применяются для передачи вращения как между параллельными, так и между перекрещивающимися валами (рис. 73). Угол наклона зyбa  обычно лежит в пределах 8–12°. На рис. 58 показаны передачи: а) – с косым зубом, в) – с шевронным зубом.

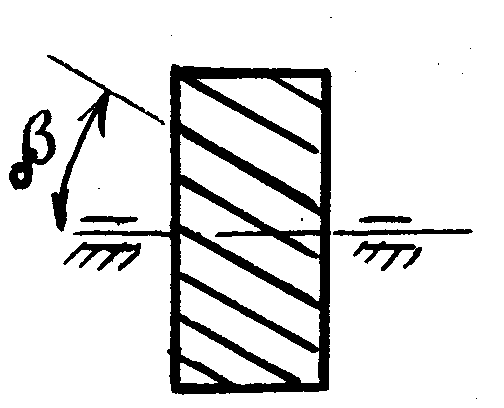
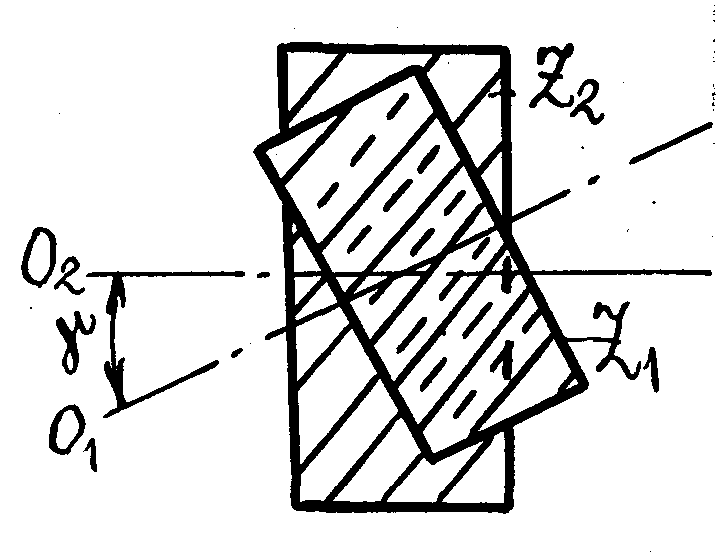
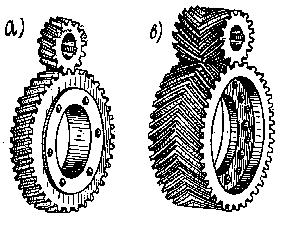
Рис. 73

Конические зубчатые колеса. Применяются для передачи вращения между пересекающимися валами. Угол между осями валов мо­жет быть любой, наиболее часто – 90°. Зубья нарезаны на усеченных конусах (начальных конусах), вершины которых совпадают (рис. 74). Передаточное число

.

Рис. 74

Червячная передача. Передача представляет собой зацеп­ление винта (с трапециевидной резьбой) с косозубым колесом, угол наклона зуба которого равен углу подъема винтовой нитки червя­ка (винта) (рис. 75).

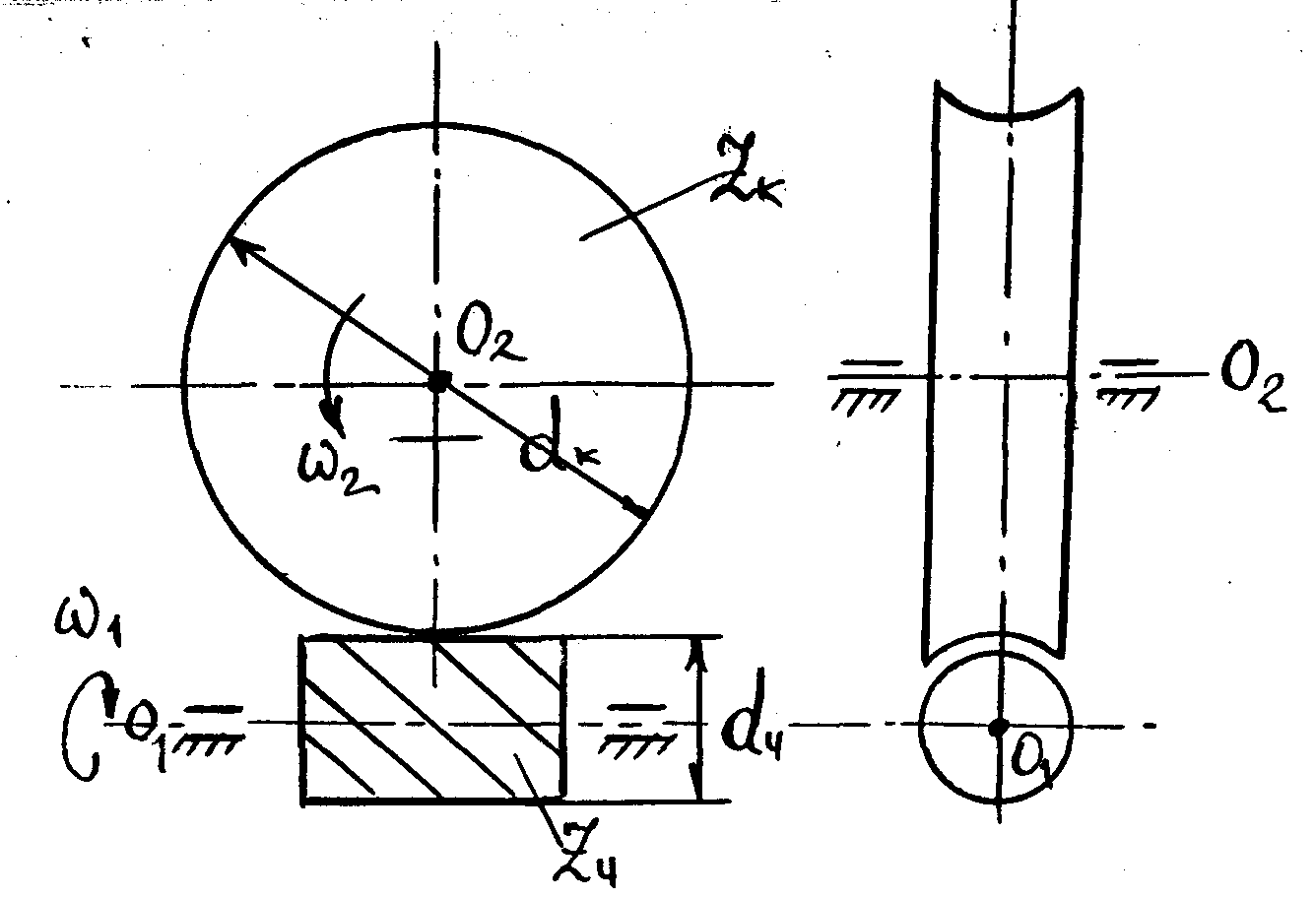
Рис. 75

Начальные диаметры червячного колеса и червяка соответственно будут

.

Здесь q – число модулей в диаметре делительного цилиндра червя­ка, q=8–12. Передаточное число червячной пары может быть достаточно большим. Обычно 10–100.

,

где z_k – число зубцов червячного колеса, z_ч – число заходов резьбы червяка (1–6).

Большое передаточное число в одной паре – основное достоинство такого механизма.

Основной недостаток червячной передачи – низкий, по современным представлениям, КПД (0,7–0,9). Это значит, что, например, при КПД=0,8 из каждых 10 кВт передаваемой мощности – 2 кВт тратятся на преодоление трения в передаче, т.е. на нагрев ее, что обычно тре­бует специальных приемов и устройств для ее охлаждения, а это вызывает дополнительные потери мощности. Низкий КПД передачи связан с тем, что движение зуба червячного колеса по виткам червяка (как движе­ние витков гайки по виткам винта) аналогично подъему груза по нак­лонной площадке (рис. 76).

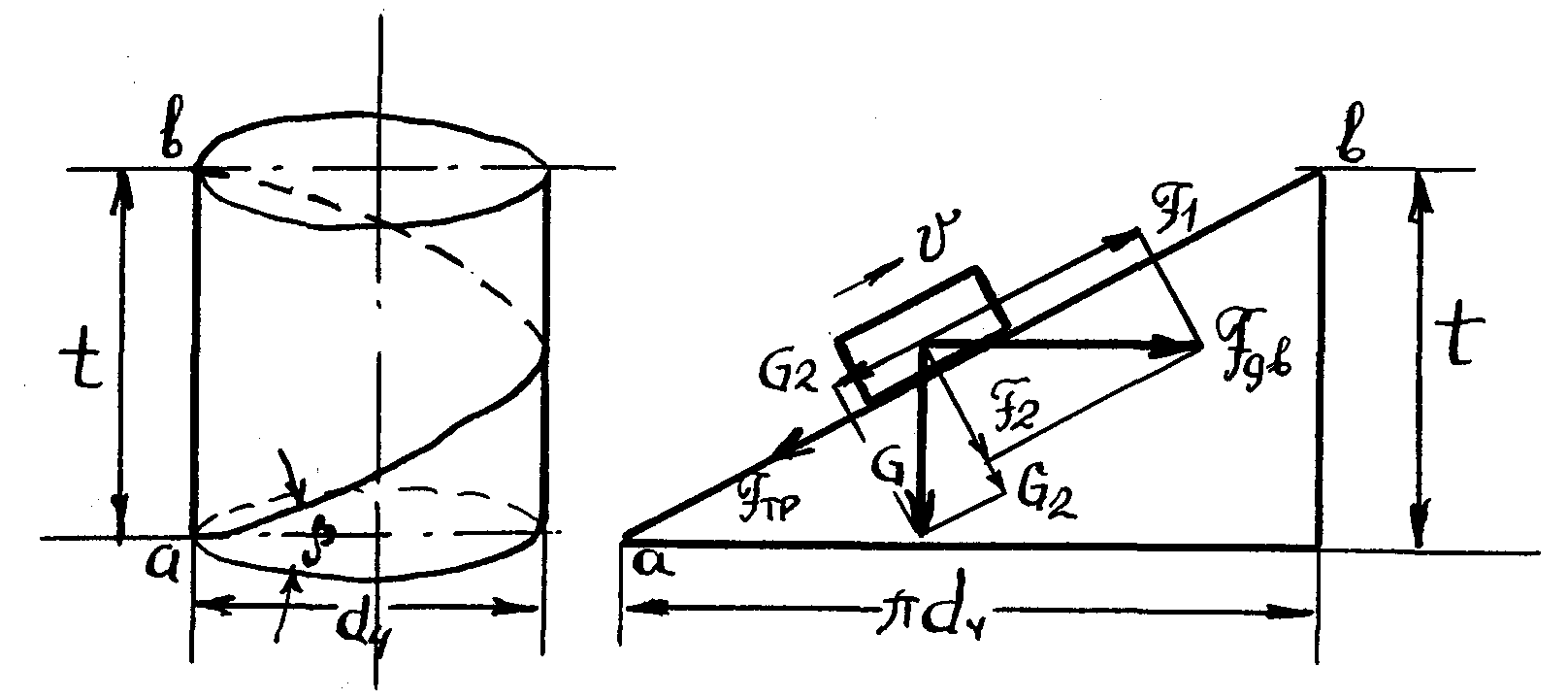
Рис. 76

КПД при движении груза по наклонной площадке вверх _вп как из­вестно равен

,

где  = arctg f – угол трения.

Таким образом, КПД червячной передачи включает в себя потери и в зубчатой, и в винтовой парах и, следовательно

.

Зубчатые передачи с подвижными осями (эпициклические).

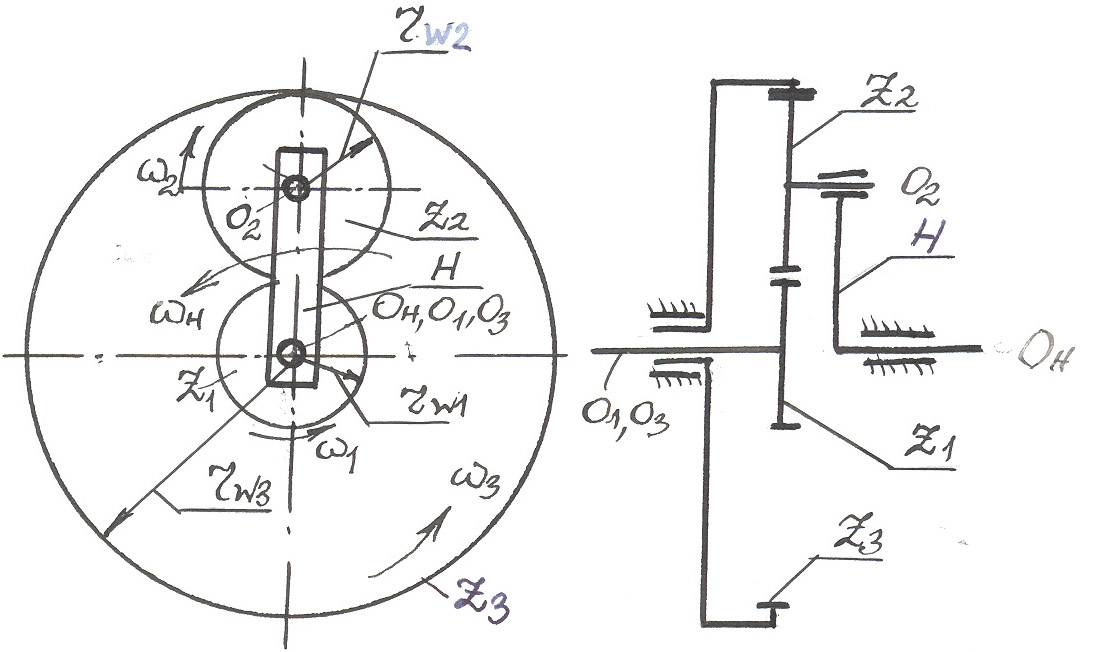
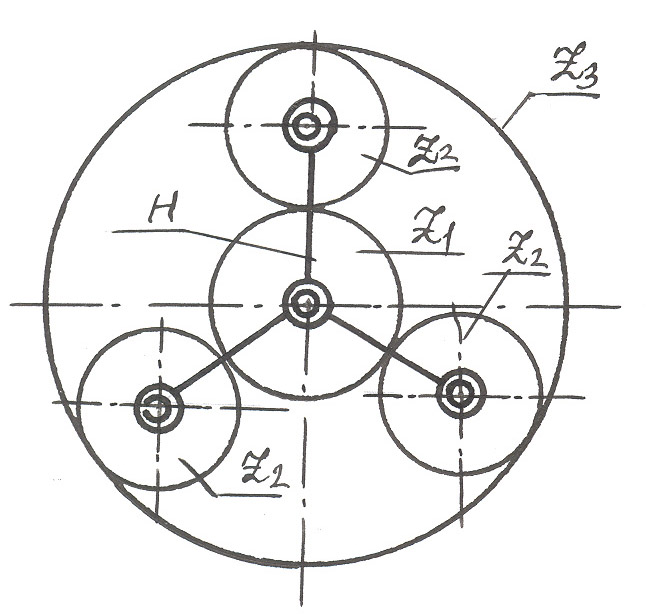
Рис. 77

Широкое применение получили зубчатые передачи с подвижными осями. Их основное достоинство – компактность при значительных передаточных числах.

В передаче звено Н вращается по оси О_н и несет на себе другую ось – О₂, которая перемещается вместе со звеном. Звено Н называется водилом или поводком, зубчатое колесо z₂ – сателлитом (их обычно бывает несколько – 3-5). Колеса z₁ и z₃ – центральными (солнечными) колесами. Таким образом, сателлит совершает сложное движение: переносное вращение вместе с водилом, несущим ось О₂ сателлита, и вращение на оси О₂ относительно поводка. Для работы такой передачи необходимо, чтобы геометрические оси О₁, О_н и О₃ совпадали. Следовательно, размеры всех звеньев не могут быть совершенно произвольными: они связаны между собой требованием соосности. Для показательной передачи это условие выражается равенством:

или

Если колесо z₃ (или z₁) сделать неподвижным, то передача будет иметь степень подвижности равную I, т.е. иметь одно ведущее звено. Если все колеса будут подвижными, то степень подвижности будет 2 и ведущих звеньев должно быть 2. В первом случае передача называется ПЛАНЕТАРНОЙ, во втором ДИФФЕРЕНЦИАЛЬНОЙ. В случае нескольких сателлитов при проектировании должны быть соблюдены так называемые условия сборки и соседства. Условие сборки требует, чтобы зубцы каждого сателлита могли одновременно войти в зацепление с обоими центральными колесами z₁ и z₃ при осесимметричном их расположении. Это будет выполнено при

К – целое число, Р – число сателлитов.

В соответствии с условием соседства, сателлиты не должны налезать друг на друга. Для этого

Для определения передаточного числа таких передач существует несколько методов. Может быть более удобным является МЕТОД ОСТАНОВА ВОДИЛА. Добавляя всем звеньям угловую скорость водила с обратным знаком (-ω_н), останавливаем водило и получаем простую передачу с неподвижными осями, в которой звенья вращаются с угловыми скоростями ω_1н, ω_2н, ω_3н. Тогда

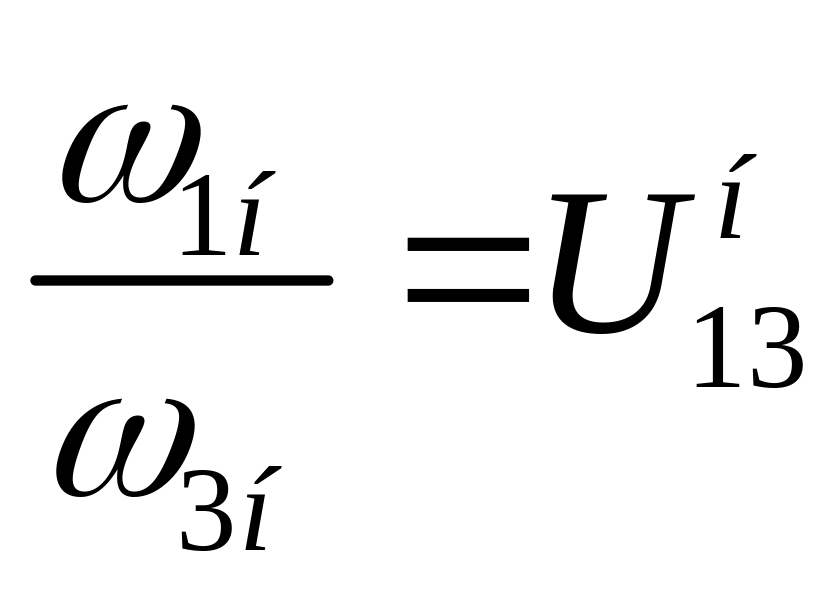или

При неподвижном колесе z₃, т.е. при ω₃=0, получаем

Отметим, что КПД планетарной передачи зависит от того, передается ли движение от центрального подвижного колеса водилу или наоборот.

Зубчатые колеса могут быть и не круглыми. Передаточное отношение в таких передачах будет переменным внутри каждого оборота. На рисунке 78 показаны такие колеса. Слева от них – мальтийский механизм.

Рис. 78