2.10. Изгиб прямого бруса

Как было сказано выше, деформация изгиба стержня возникает от нагрузок, действующих в его осевой плоскости и пер­пендикулярных к его оси. В частном случае, когда изгибающие наг­рузки являются только парами сил, изгиб называется чистым. В общем случае, когда действующая система нагрузок состоит из сил и пар, изгиб называется поперечным. Стержень, работающий на изгиб, принято называть балкой.

Напряжения при чистом изгибе. Простейшая схема выглядит так (рис. 31).

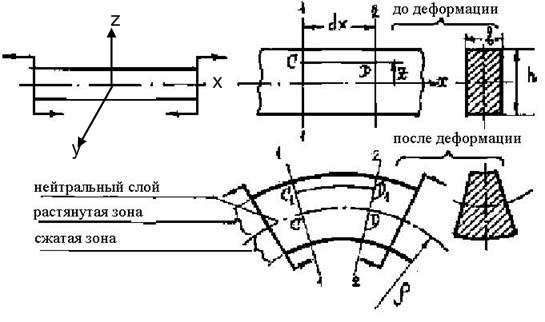
Рис. 31

Под действием внешних сил (момента) балка деформируется, ее прямолинейная ось (х–х) искривляется. В результате деформиро­вания в балке возникают растянутая и сжатая зоны. Продольные элементы балки будут удлиняться в одной зоне и укорачиваться в другой. Средний слой, который не испытывает при изгибе ни растяжения, ни сжатия, называется нейтральным слоем.

Экспериментальные исследования чистого поперечного изгиба балок позволяют принять следующие положения:

1. Поперечные сечения балки, плоские до деформации, остаются плоскими и после деформации (так называемая гипотеза плоских сечений).

2. По ширине поперечного сечения напряжения не изменяются.

3. Продольные элементы балки друг на друга не надавливают, а испытывают обычное растяжение или сжатие.

Эти предпосылки, по существу, определяют характер распределения напряжений по сечению балки, что вместе с условиями равновесия позволяет найти их величину.

Используя метод сечений и действуя по той же схеме, что и при кручении, получим формулу для определения нормальных напряжений в любой точке поперечного сечения балки

.

Эпюра нормальных напряжений показана на рис. 32.

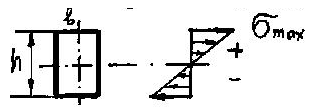
Рис. 32

Таким образом, напряжения по высоте сечения меняются по линейному закону. Обозначим

, тогда ,

где W_y – осевой момент сопротивления, например, для прямоугольного сечения

,

и для круглого

.

Условие прочности будет

.

Напряжения при поперечном изгибе. При чистом изгибе в сечениях есть только один силовой фактор – изгибающий момент М. При поперечном изгибе в сечениях балки есть два силовых фактора – изгибающий момент М и перерезывающая сила F_z. Изгибающему моменту соответствует нормальное напряжение. По-видимому, перерезывающей силе будут соответствовать касательные напряжения.

Допускаем, что нормальные напряжения для общего случая плоского изгиба могут быть определены по формуле чистого изгиба

,

где М(х) – изгибающий момент в рассматриваемом сечении; Z – расстояние от нейтральной оси до точки, в которой определяется напряжение; I_y – момент инерции сечения относительно нейтральной оси.

Определим касательные напряжения. Опуская несложные преоб­разования, получим

,

где I_y – осевой момент инерции, S – статический момент площади относительно нейтральной оси.

Для прямоугольного сечения

, , где , .

Тогда

, где А=bh и .

Для балки круглого сечения , где .

Условие прочности .

Часто влиянием перерезывающей силы пренебрегают. Однако, влиянием перерезывающей силы не всегда можно пренеб­речь. Если для некоторого симметричного относительно оси Оу сечения ось Оz не являетcя осью симметрии, то главный вектор касательных напряжений в этом случае, определяе­мых перерезывающей силой F, параллельной оси О, проходит не через центр тяжес­ти сечения, а через некоторую точку "С" на оси Оу, называемую центром кручения. Если внешние нагрузки располагается в плоскости, параллельной оси Оz, прохо­дящей через центр кручения, главный вектор касательных напряжений эквивалентен перерезывающей силе; в противном случае в балке возника­ют крутящие усилия. Например, для показанного на рис. 33 сечения положение центра кручения определится так

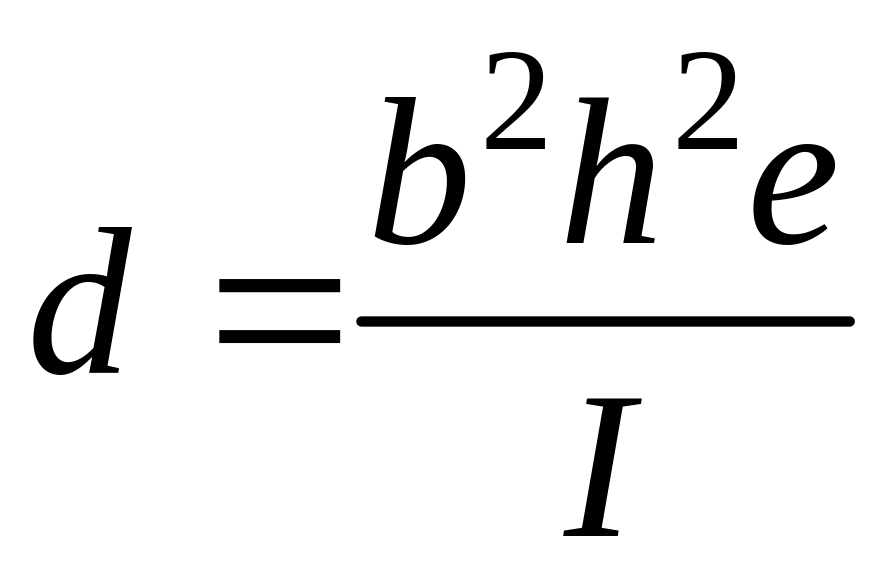
I - момент инерции сечения отно­сительно оси О.

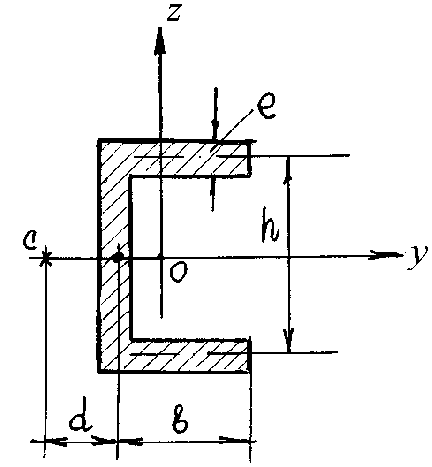
Рис. 33