Приближение слабосвязанных электронов.

В приближении слабосвязанных электронов электронные облака валентных электронов размазаны по всему объему у кристалла равномерно. Потенциальная энергия электронов в этом случае, запишется:

,

где U₀ – потенциальная энергия электронов в результирующем поле положительных ионов, U(r) - приращение потенциальной энергии, учитывающее взаимодействие атомов.

Уравнение Шредингера относительно амплитудной волновой функции в приближении слабосвязанных электронов запишется

.

Это уравнение является линейным дифференциальным уравнени-ем в частных производных с переменными коэффициентами. Решение этого уравнения ищется в виде функций Блоха:

,

где U(r) – периодическая функция с периодом равным постоянной решетки:

,

где – вектор трансляции. В этом выражении n₁, n₂, n₃ – произвольные целые числа, – векторы элементарных трансляций.

Движение электрона в кристаллической решетке Модель Кронига-Пенни

Модель Кронига-Пенни заменяет линейную одномерную цепочку атомов кристаллической решетки цепочкой потенциальных ям и по-тенциальных барьеров и рассматривает движение электрона, обладаю-щего энергией E, вдоль этой цепочки.

Р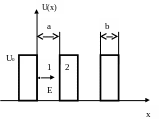 ис.1. Цепочка потенциальных барьеров и ям

Уравнение Шредингера для модели Кронига-Пенни

При рассмотрении движения электрона вдоль цепочки потен-циальных ям и потенциальных барьеров воспользуемся приближени-ем слабо связанных электронов. Уравнение Шредингера для этого случая запишется:

.

В первом приближение будем полагать, что взаимодействие меж-ду атомами отсутствует. Тогда уравнение Шредингера примет вид

.

Так как операции интегрирования и дифференцирования должны осуществляться в областях, где функции и их первые производные непрерывны, то рассмотрим это уравнение для области вне потенциального барьера 1 и внутри потенциального барьера 2. Для области вне потенциального барьера обозначим волновую функцию ₁(x), а для области внутри потенциального барьера – ₂(x). Уравнения Шредингера для этих областей запишутся:

Введем обозначения:

Тогда получим:

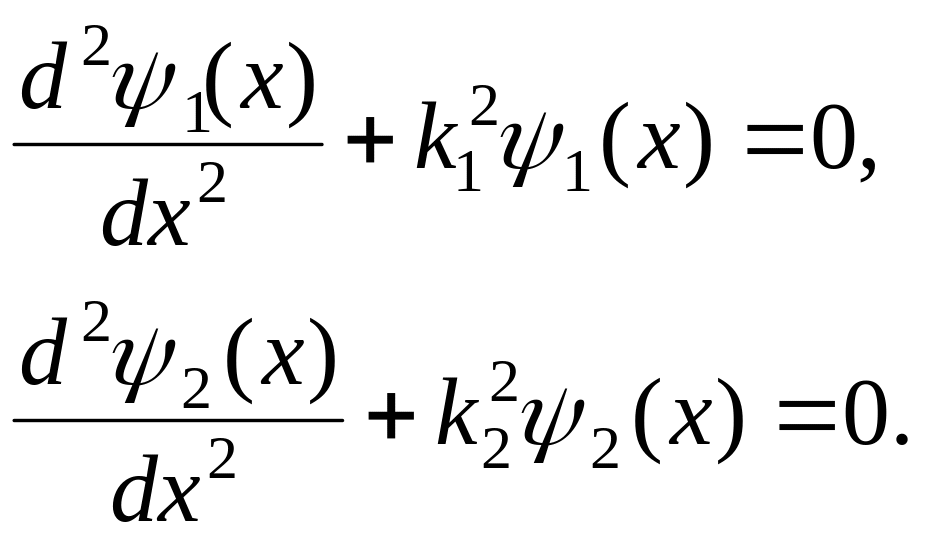
Решение уравнения Шредингера

Решение уравнений при отсутствии взаимодействия между атомами будут иметь вид:

Если теперь принять во внимание взаимодействие между атомами, то решения уравнений следует искать в виде функций Блоха:

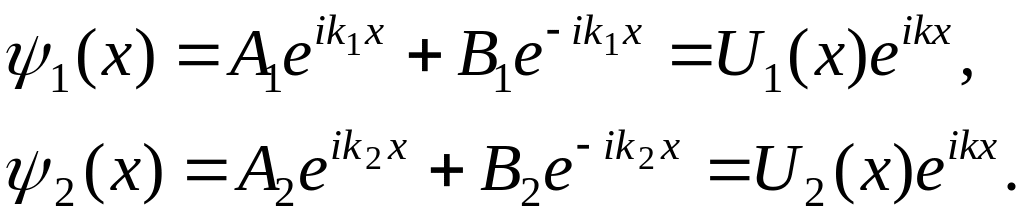
Откуда для функций Блоха можно записать:

Определение волнового числа

Постоянные интегрирования A₁, A₂, B₁, B₂, k определяются из граничных условий. Используя граничные условия, можно получить следующее трансцендентное уравнение относительно волнового числа k:

.

Устремим b 0 и U₀  так, чтобы произведение

оставалось конечным. Это эквивалентно представлению линейки по-тенциальных ям и потенциальных барьеров в виде последовательнос-ти чередующихся потенциальных барьеров, имеющих вид дельта- функции:

; .

Г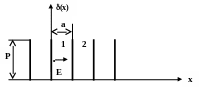 рафик этих функций имеет вид:

Рис.2. Цепочка дельтообразных потенциальных барьеров

Тогда трансцендентное уравнение относительно волнового числа k примет вид

.

Оценим графически решение данного уравнения. Для этого необходимо построить графики левой части и правой части этого уравнения. Обозначим через f₁(k₁a) и f₂(ka) правую и левую части этого уравнения:

Поскольку величина волнового числа k неизвестна, то график изменения правой части невозможно построить, а могут быть определены пределы изменения функции f₂(k·a) – (+1, –1). Построим график функции f₁(k₁a) и на этом графике определим пределы изменения функции f₂(ka). Области пересечения графика функции f₁(k₁a) и пределов изменения функции f₂(ka) определяют области значений волнового числа k.

Р ис.3. Графическое решение

Из рисунка 3 видно, что волновое число k наряду с дискретными значениями имеет области разрешенных непрерывных значений. Кроме того, волновое число имеет области запрещенных значений.

Энергетические зоны модели Кронига-Пенни

Энергия свободного электрона, выраженная через импульс, определяется

.

Это выражение в координатах энергии и волнового числа пред-ставляет параболу. С другой стороны, для кристалла с периодическим повторением расположения атомов волновое число может быть определено из выражения:

.

Подставляя волновое число в значение энергии, получим:

.

Решение уравнения Шредингера для электрона, двигающегося в пространстве кристаллической решетки, характеризуется наличием разрешенных и запрещенных значений волновых чисел, а, следовательно, разрешенных и запрещенных значений энергий. Области разрешенных и запрещенных значений энергий формируют соответствующие зоны – зоны разрешенных энергий E₁, E₂, E₃ и зоны запрещенных энергий (см. рисунок 4).

Рис.4. Вид разрешенных и запрещенных областей