Лабораторная работа №2 движение микрочастиц в поле потенциальных сил. Движение микрочастиц через потенциальный барьер Определение потенциального барьера

Одной из разновидностей движения частиц в поле потенциаль-ных сил является движение частиц через потенциальный барьер.

Потенциальным барьером называется область пространства, в которой потенциальная энергия изменяется либо скачком, либо по ка-кому-то закону. Потенциальный барьер означает, что силы действуют на частицу в некоторой области пространства. Вне этой области час-тица движется свободно.

Бесконечно протяженный потенциальный барьер характеризует-ся равенством нулю потенциальной энергии частицы, находящейся вне потенциального барьера. Если частица находится внутри потен-цииального барьера, ее потенциальная энергия равна бесконечности.

Для конечных потенциальных барьеров потенциальная энергия частицы внутри этого барьера равна конечному значению.

Физическими примерами движения микрочастиц через потенци-альный барьер является движение электронов через границу раздела двух полупроводников с различными типами электропроводности, прохождение микрочастиц через тонкие пленки.

Прохождение микрочастиц (квантово-механических частиц) че-рез потенциальный барьер существенно отличается от прохождения классических частиц.

В классической механике частица, двигающаяся вне области по-тенциального барьера и с энергией меньшей энергии потенциального барьера, при приближении к потенциальному барьеру полностью отражается от него. В этом случае область потенциального барьера яв-ляется полностью недоступной для частицы, так как в этой области полная энергия частицы меньше энергии потенциального барьера.

Квантово-механическая частица, двигающаяся по законам кван-товой механики, с определенной вероятностью может проникнуть в область потенциального барьера даже при полной ее энергии меньшей энергии потенциального барьера.

Если полная энергия классической частицы будет больше энер-гии потенциального барьера, частица беспрепятственно проходит через потенциальный барьер. При этом ее энергия в области потен-циального барьера будет меньше на величину энергии потенциально-го барьера.

Для квантово-механической частицы и в этом случае имеется ве-роятность отражения частицы от потенциального барьера.

При равенстве энергии частицы и энергии потенциального барь-ера классическая частица пройдет в область потенциального барьера. Однако кинетическая энергия частицы в этом случае в области потен-циального барьера будет равна нулю.

Для квантово-механической частицы коэффициент отражения будет равен единице.

Уравнение Шредингера для частицы двигающейся через потенциальный барьер

Рассмотрим движение частицы, имеющей энергию E и двига-ющейся вдоль оси x к потенциальному барьеру с энергией U₀ (см. ри- сунок 1).

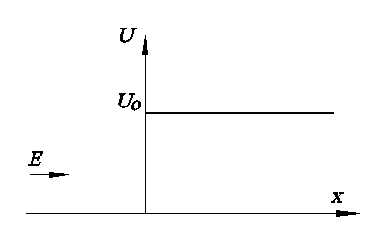
Ри.1. Движение частицы через потенциальный барьер

Потенциальный барьер, в этом случае, задается в виде:

(1)

Для частицы, двигающейся через потенциальный барьер в на-правлении оси x, уравнение Шредингера запишется:

. (2)

Обозначим волновую функцию для области вне потенциального барьера как и волновую функцию в области потенциального барьера как , получим уравнение Шредингера для области вне потенциального барьера и для области потенциального барьера:

, (3)

. (4)

Введем обозначения:

, . (5)

Тогда уравнения перепишутся:

, (6)

. (7)

Решение этих уравнений имеет вид

, (8)

, (9)

где A₁,A₂,B₁,B₂ – постоянные интегрирования. Для определения по-стоянных интегрирования исследуется поведение волновой функции на границе области x=0.

Слагаемые, содержащие положительные экспоненты, определяют плоские волны, распространяющиеся в положительном направлении оси x – падающие волны.

Слагаемые, содержащие отрицательные экспоненты, определя-ют плоские волны, распространяющиеся в обратном направлении оси x – отраженные волны.

Величина A₁ является амплитудой падающей волны. Зададимся значением этой амплитуды, равной единице A₁=1.

Так как в области потенциального барьера какие-либо препят-ствия распространению волны отсутствуют, то в этой области ампли-туду отраженной волны можно приравнять к нулю B₂=0.

Волновая функция и ее производные должны оставаться непре-рывными, даже в точках разрыва потенциальной энергии:

, . (10)

Подставляя граничные условия в решения уравнения Шрединге-ра, получим:

, ,

, . (11)

Подставляя эти значения в граничные условия и решая систему уравнений, получим:

, . (12)

Из этих выражений видно, что коэффициент B₁, характеризую-щий амплитуду отраженной волны от потенциального барьера, будет отличен от нуля. Это обусловлено волновыми свойствами микрочас-тиц.