§5. Силы, возникающие на кривой поверхности жидкости
Кривизна поверхности жидкости приводит к появлению сил, действующих на жидкость под этой поверхностью.
Р
ассмотрим
сферическую каплю радиусом
(рис.7).
При увеличении
радиуса сферы растет площадь его
поверхности, а вместе с ней и поверхностная
энергия. А
это может происходить только за счет
совершения работы внешними силами.
Наоборот, при уменьшении радиуса капли
поверхностная энергия уменьшается. Это
значит, что работа производится силами,
действующими в самой капле. Если
на каплю не действуют внешние силы, то
они стремятся занять наименьший объем,
т.е. объем жидкости под сферической
поверхностью всегда несколько сжат.
Это приводит к тому, что жидкость в капле
испытывает дополнительное давление,
направленное радиально перпендикулярно
к ее поверхности. Пусть под действием
этого давления жидкий шар уменьшит
объем на
.
При этом производится работа сжатия
жидкости за счет уменьшения поверхностной
энергии капли. Работа сжатия
равна:
,
(6.7)
а уменьшение
поверхностной энергии
равна:
, (6.8)
где
- уменьшение
поверхности шара, связанное с уменьшением
радиуса капли на
.
Для шара
и
.
Отсюда следует:
.
Подставляя эти
значения для
и
в (6.7) и (6.8) и
принимая во внимание, что
,
получаем:
,
откуда имеем для давления, оказываемого на жидкость ее кривой поверхностью следующее выражение:
.
(6.9)
Если поверхность жидкости цилиндрическая, то
,
где - длина цилиндра. Соответственно
.
Подставляя эти значения и в формулы (6.7) и (6.8) аналогично получим:
.
(6.10)
В общем случае поверхности любой формы давление, обусловленное кривизной поверхности, выражаются уравнением, известным под названием уравнения Лапласа:
,
(6.11)
где
и
- главные
радиусы кривизны для данного элемента
поверхности.
В случае сферы = и формула (6.11) переходит в (6.9). В случае цилиндра один из главных радиусов равняется , а другой совпадает с радиусом цилиндра. Соответственно, формула (6.11) переходит в (6.10). Дополнительное давление, определяемое формулой (6.11) направлено к центру кривизны поверхности.
§6. Капиллярные явления
В случае, когда жидкость находится в узком сосуде, влияние стенок простирается на всю поверхность жидкости, и она оказывается искривленной на всем своем протяжении.
Если размеры сосуда, в котором находится жидкость, сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярными. Явления, происходящие в таких сосудах, называются капиллярными явлениями.
Рассмотрим некоторые явления, связанные с капиллярностью.
П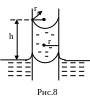
оскольку
в капиллярных сосудах жидкость имеет
кривую поверхность, здесь появляется
дополнительное давление, вызванное
кривизной поверхности. Следствием этого
является капиллярный подъем. На рис.8
изображена узкая труба, опущенная в
широкий сосуд с жидкостью. Пусть стенки
сосуда смачиваются жидкостью. Тогда
жидкость, протекающая в трубку, образует
вогнутый мениск. Пусть трубка настолько
узка, что ее радиус сравним с радиусом
мениска.
Вследствие кривизны мениска
появляется дополнительное давление,
направленное к центру кривизны мениска,
т.е. вверх, равное
.
Под действием этого давления жидкость
поднимается по трубке до уровня
,
при котором гидростатическое давление
столба
жидкости высотой
,
уравновешивают избыточное давление,
т.е.
,
(6.12)
где
- плотность
жидкости,
- ускорение
свободного падения. Из (4.12) следует, что
высота подъема жидкости
будет равна
.
(6.13)
Поскольку радиус
кривизны
трудно
определить экспериментально, появляется
необходимость выражения
через радиус
трубки
.
Для этого воспользуемся рисунком 9.
Ц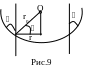
ентр
сферы, частью которой является мениск,
находится в точке О.
Краевой угол жидкости, соприкасающийся
со стенками капилляра, равен
.
Из чертежа видно, что
.
Поэтому формулу (6.13) можно переписать
в виде:
.
(6.14)
Для жидкости,
полностью смачивающей стенки капилляра
=0,
и
.
(6.15)
Как следует из (6.15), высота подъема жидкости будет тем больше, чем меньше радиус капилляра и больше коэффициент поверхностного натяжения.
Если жидкость не смачивает капилляр, то картина будет обратной, так как мениск будет выпуклой, а центр кривизны будет находиться внутри жидкости, и давление Лапласа будет направлено вниз. Уровень жидкости в
к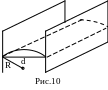
апилляре
будет ниже уровня в сосуде, в который
определен капилляр. Разность уровней
в этом случае будет также определяться
формулой (6.14) или (6.15). Жидкость может
подняться вверх и в том случае, когда
она находится между пластинами,
разделенными узким зазором. Если пластины
параллельны друг другу, то мениск имеет
цилиндрическую форму, соответственно,
дополнительное давление будет равно
,
где
-радиус
мениска. Условие равновесия требует
выполнения условия:
,
(6.16)
откуда
.
Из рисунка 10 видно, что
,
где
-
расстояние между пластинами. Тогда
высоту подъема жидкости можно определить
по формуле
.
(6.17)