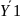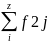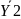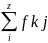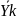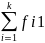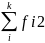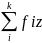- •Статистика наука о массовых явлениях
- •Способы получения статистической информации (отчетность обследования)
- •Статистическая совокупность (единица совокупности, виды признаков)
- •Виды статистического наблюдения
- •Ошибки статистического наблюдения.
- •Статистическая сводка и группировка
- •Абсолютные и относительные статистические величины
- •Средние величины на базе степенной средней
- •Вычисление средней арифметической при различных вариантах задания исходных данных и их свойства
- •Порядковые статистики. Квартили. Децили. Способы определения по выборочным данным.
- •Мода, определение по статистическим данным, свойства использования в статистическом анализе.
- •Медиана, определение по статистическим данным, свойства использования в статистическом анализе
- •Вариация признаков- важнейшее свойство единиц статистической совокупности
- •Показатели вариации, наиболее часто употребительные в статистике
- •Дисперсия и среднее квадратическое отклонение
- •Коэффициенты вариации, свойства, области применения
- •Графическое представление вариационного ряда
- •Асимметрия распределения (As )
- •Эксцесс распределения (куртозис, Ex)
- •Сглаживание эмпирического распределения нормальным законно распределения
- •Понятие статистической гипотезы и статистического критерия, как инструмента проверки статистических гипотез
- •Проверка гипотезы о законе распределения
- •Ошибки первого и второго рода при проверке статистических гипотез
- •Критерий согласия Xи квадрат (Критерий к. Пирсона).
- •Выборочный метод
- •Виды выборочного статистического исследования
- •Способы обеспечения случайного отбора при формирования выборки.
- •Расслоенная выборка. Способы формирования выборки при расслоенном отборе
- •Доверительный интервал для генеральной средней.
- •Определение необходимого объема выборки.
- •Повторная и бесповторная выборка
- •Средняя ошибка выборки
- •Предельная ошибка выборки.
- •Малая выборка.
- •36. Парная корреляция и регрессия.
- •37.Оценка тесноты связи в задаче парной корреляции
- •38.Соотношение коэффициента корреляции и корреляционного отношения.
- •39. Коэффициент детерминации.
- •40. Оценка существенности корреляционной связи.
- •41.Доверительный интервал для генерального коэффициента корреляции
- •42.Оценка параметров линейной регрессии.
- •43.Корреляционная таблица
- •44.Эмпирическая регрессия.
- •45.Интерпритация правила сложения дисперсий в контексте задачи анализа корреляций.
- •46.Эмпирическое корреляционное отношение.
- •47.Теоретическое корреляционное отношение
- •48.Оценка значимости коэффициента корреляции
- •49.Ранговые коэффициенты корреляции
- •50.Остаточная дисперсия
- •52.Оценка существенности параметров линейной регрессии.
- •54.Оценка тесноты связи в случае альтернативной вариации
- •55.Множественный коэффициент корреляции
- •56.Частная корреляция.
- •58.Компоненты динамического ряда
- •59. Показатели динамического ряда: абсолютный прирост, средний абсолютный прирост, темпы роста и прироста и их среднее значение.
- •61.Приемы выявление сезонной составляющей динамического ряда
- •62. Аналитическое сглаживание динамических рядов.
- •63. Выбор наилучшего тренда из набора возможных.
- •65. Автокорреляция в динамических рядах.
- •67. Анализ взаимосвязанных динамических рядов (кросс-корреляция).
- •68. Прогнозирование по тренду.
- •69. Доверительный интервал для прогнозных значений.
- •71. Индексы цепные, базисные, индивидуальные и сводные, переменного и фиксированного
- •72. Индекс физического объёма продукции.
- •73. Индекс цен (Схема Пааше и Ласпейреса).
- •74. Взаимосвязь индекса цен и индекса физического объема продукции.
- •75. Индекс себестоимости
40. Оценка существенности корреляционной связи.
Вычисление в каждой задачи
коэффициента корреляции является
выборочным (другими словами) точечная
оценка неизвестного генерального
коэффициента корреляции. В связи с этим
возникает необходимые оценки существования
корреляционной связи или проверки
гипотезы H0
:c=0 Гипотеза
проверяется с помощью t-статистики
t=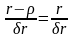 δr=
δr=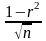
41.Доверительный интервал для генерального коэффициента корреляции
Можно построит доверительный интервал
r-t δr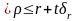
Доверительные интервалы строятся на нормальном распределении параметра. В случае коэф. корреляции задача построения доверительного интервала осложняется, в связи с тем распределения очень сложно. При небольших значениях коэф. Корреляции распределены нормально, при очень больших значениях коэффициента корреляции выборочное распределены резко ассиметрично.
42.Оценка параметров линейной регрессии.
Линейная зависимость — наиболее часто используемая форма связи между двумя коррелируемыми признаками, и выражается она, как указывалось ранее, при парной корреляции уравнением прямой:
Гипотеза именно о линейной зависимости между х и у выдвигается в том случае, если значения результативного и факторного признаков возрастают (или убывают) одинаково, примерно в арифметической прогрессии.
Параметры
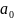 и
и
 отыскиваются по МНК
следующим образом. Согласно требованию
МНК при линейной зависимости в формуле
вместо
отыскиваются по МНК
следующим образом. Согласно требованию
МНК при линейной зависимости в формуле
вместо
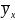 записываем
его конкретное выражение:
записываем
его конкретное выражение:
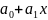 .
Тогда
.
Тогда
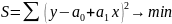
Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении и . функция двух переменных S может достигнуть минимума.
Как известно, для этого надо найти частные производные S по и , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с изложенным
найдем частные производные

Сократив каждое уравнение
на —2, раскрыв скобки и перенеся члены
с х в одну сторону, а с у
- в другую, получим
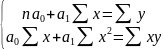
Эта система называется системой нормальных уравнений МНК для линейного уравнения регрессии.
Для решения системы по
эмпирическим данным определяем число
единиц наблюдения п,
сумму значений
факторного признака
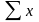 ,
сумму их квадратов
2
, а также сумму значений результативного
признака
,
сумму их квадратов
2
, а также сумму значений результативного
признака
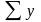 и сумму произведений
и сумму произведений
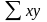 .
.
Подставив все эти суммы в систему нормальных уравнений, найдем параметры искомой прямой (линейного уравнения регрессии).
При этом указанные суммы можно определить двумя способами:
• по данным о значениях х и у каждой единицы совокупности;
• по сгруппированным данным, представленным в виде корреляционной или иной таблицы.
43.Корреляционная таблица
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:
X\Y |
Y1 |
Y2 |
... |
Yz |
Итого |
Yi |
X1 |
f11 |
12 |
... |
f1z |
|
|
X1 |
f21 |
22 |
... |
f2z |
|
|
... |
... |
... |
... |
... |
... |
... |
Xr |
fk1 |
k2 |
... |
fkz |
|
|
Итого |
|
|
... |
|
n |
|
|
|
|
|
|
|
- |
В основу группировки положены два изучаемых во взаимосвязи признака – Х и У. Частоты fij показывают количество соответствующих сочетаний Х и У. Если fij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания fij допустимо утверждать о связи между Х и У. При этом, если fij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.