37.Оценка тесноты связи в задаче парной корреляции

Изучение корреляционных связей сводится в основном к ре­шению следующих задач:

• выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками. Эта задача может быть решена на основе параллельного сопоставления (сравнения) значений у и у в каждой из п единиц совокупности, а также с помощью группировок и путем построения и анализа специальных корре­ляционных таблиц;

• измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов. Эта часть исследова­ния именуется корреляционным анализом;

• определение уравнения регрессии - математической модели, е которой среднее значение результативного признака у рассма­тривается как функция одной или нескольких переменных-факторных признаков. Эта часть исследования именуется ре­грессионным анализом.

Последовательность рассмотрения перечисленных задач, есте­ственно, может меняться в каждом конкретном исследовании.

38.Соотношение коэффициента корреляции и корреляционного отношения.

N теоретическое корреляционное отноше­ние позволяет измерять тесноту зависимости при любой форме связи.

Нетрудно доказать, что при линейной зависимости теоретиче­ское корреляционное отношение тождественно линейному коэф­фициенту корреляции, т.е. η_теор = r. Для этого преобразуем фор­мулу

Учитывая, что при линейной зависимости и

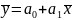
отсюда

Линейный коэффициент корреляции в виде выступает в роли стандартизированного коэффициента регрессии, т.е. показывает, на сколько «сигм» изменится в среднем у при уве­личении хна одну «сигму» (среднее квадратическое отклонение в ряду х).

39. Коэффициент детерминации.

Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсий. Это соотношение называется эмпирическим коэффициентом детерминации η²_эмп и показывает, ка­кая доля в общей дисперсии приходится на дисперсию, обуслов­ленную вариацией признака, положенного в основу группировки:

Используется правило сложения дисперсий и для определения степени связи между изучаемыми признаками. Для этого необхо­димо найти эмпирическое корреляционное отношение η_эмп, которое показывает, насколько тесно связаны исследуемое явление и группировочный признак:

Теоретическое корреляционное отношение представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических зна­чений результативного признака со средним квадратическим от­клонением в ряду эмпирических значений (или корень квадрат­ный из отношения дисперсий теоретического и эмпирического ряда значений результативного признака). Так как суммы теоретических и эмпирических значений ре­зультативного признака совпадают, т.е. , то и среднее значение признака у этих рядов одинаково — у. Если обозначить дисперсию эмпирического ряда игреков че­рез σ²_y(или D _y,), а теоретического ряда — через δ² (или D _x ), то каждая из них выразится формулами

Сравнивая вторую дисперсию с первой, получим теоретичес­кий коэффициент детерминации или

Если учесть, что σ²_y (или D _y ) - дисперсия эмпирического ряда игреков - характеризует вариацию результативного признака за счет всех факторов, включая и фактор х, т.е. измеряет общую вариацию величины у, а дисперсия теоретического ряда, т.е. δ² (или D _x) характеризует вариацию результативного признака за счет вариации только фактора х (при прочих равных услови­ях), то отношение второй дисперсии к первой, т.е. коэффициент показывает, какую долю в обшей дисперсии результативного признака занимает дисперсия, выража­ющая влияние вариации фактора х на вариацию у.

Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение или