
- •Вопрос №1
- •Вопрос №2
- •Вопрос №4
- •Вопрос №6
- •Вопрос №7
- •Вопрос №8
- •Вопрос №9
- •Вопрос №10
- •Вопрос 11
- •Вопрос12
- •Вопрос №13
- •Вопрос №14
- •Вопрос №15
- •Вопрос №16
- •Вопрос 18
- •Вопрос №17
- •Вопрос №19
- •Вопрос №20
- •Вопрос №21
- •Эквивалентное преобразование источников электрических сигналов
- •Вопрос 22
- •Вопрос23
- •Вопрос24
- •Вопрос №25
- •Вопрос №26
- •Вопрос №27
- •Вопрос №28
- •Вопрос №29
- •Вопрос №30
- •Вопрос №31
- •Вопрос №32
- •Вопрос №34
- •2. Законы Кирхгофа в комплексной форме.
- •Вопрос 35
- •Вопрос 36
- •4. Комплексная мощность. Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
- •Вопрос 37
- •Вопрос 38 Параметры двухполюсника
- •Вопрос 39
- •Вопрос 40 Параметры четырехполюсника
- •Вопрос 41 Частотные характеристики четырехполюсников
- •Вопрос 42
- •Вопрос 43 Последовательный колебательный контур состоит из последовательного соединения индуктивности l и емкости c (рис. 5.17).
- •Вопрос 49
- •Спектральный метод анализа
- •Основные определения нелинейных цепей
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Вопрос 53
- •Вопрос 54
- •Классический метод анализа
- •Спектральный метод анализа
- •Вопрос 55
- •Вопрос 56 Метод интеграла Дюамеля
- •Вопрос 58
- •Вопрос 59-62
- •Передача импульсных сигналов через дифференцирующую цепь
- •Передача импульсных сигналов через интегрирующую цепь
- •Вопрос 63-65
- •Вопрос 66
- •Вопрос 67
- •Схемы замещения по заданной топологии
- •Формальные схемы замещения
- •Вопрос 68
- •Основные понятия для идеальных фильтров
- •Классификация фильтров электрических сигналов
- •Вопрос 69
- •Понятие о длинной линии и распространение волн в ней
- •Вопрос 70-72
- •Понятие о длинной линии и распространение волн в ней
- •Полубесконечная длинная линия
- •Линия конечной длины. Отражения
- •Режимы работы длинной линии
- •Коэффициент бегущей волны и коэффициент стоячей волны
- •Применение длинных линий
Понятие о длинной линии и распространение волн в ней
Рассмотрим воздушную двухпроводную линию, длина которой соизмерима или больше длины электромагнитной волны (рис. 9.1, а). При протекании тока по проводам вокруг них возникает магнитное поле Н, что свидетельствует о наличии индуктивности, распределенной вдоль линии. Между проводами возникает электрическое поле, что говорит о емкости. Провода и диэлектрик между проводами нагреваются, что свидетельствует о наличии потерь, т.е. говорит о сопротивлении.
H
E
X
İ2
E0
zi
zн
dx
0
dx
L0dx
R0dx
C0dx
G0dx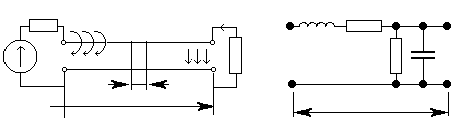
Количественно физические параметры длинной линии характеризуются следующими погонными параметрами, т.е. параметрами, приходящимися на единицу длины:
L0 – погонная индуктивность. Определяется как индуктивность короткозамкнутого отрезка линии длиной 1 м. Единица измерения Гн/м.
R0 – погонное сопротивление. Определяется как сопротивление короткозамкнутого отрезка проводов длиной 1 м. Единица измерения Ом/м.
C0 – погонная емкость. Определяется как емкость между проводами разомкнутого на конце отрезка линии длиной 1 м. Единица измерения Ф/м.
G0 – поперечная проводимость. Определяется как проводимость между проводами, разомкнутыми на конце отрезка линии длиной 1 м. Единица измерения См/м.
Выделим участок длины dx. Его можно представить эквивалентной схемой, приведенной на рис. 9.1, б.
Е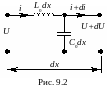 сли
погонные параметры не зависят от x,
то линии называются однородными, если
погонные параметры зависят от координаты
х,
неоднородными. Если R0
= G0
= 0, то линию
называют линией без потерь.
сли
погонные параметры не зависят от x,
то линии называются однородными, если
погонные параметры зависят от координаты
х,
неоднородными. Если R0
= G0
= 0, то линию
называют линией без потерь.
Составим уравнения, позволяющие определить напряжение и ток в любом сечении длинной линии, для длинной линии без потерь (рис. 9.2). Запишем выражения относительно приращений напряжения и тока:
![]() ;
(9.1)
;
(9.1)
![]() .
(9.2)
.
(9.2)
Поделим первое и второе уравнение на dx, а затем продифференцируем первое уравнение по х, второе – по t, а затем выразим смешанные производные:
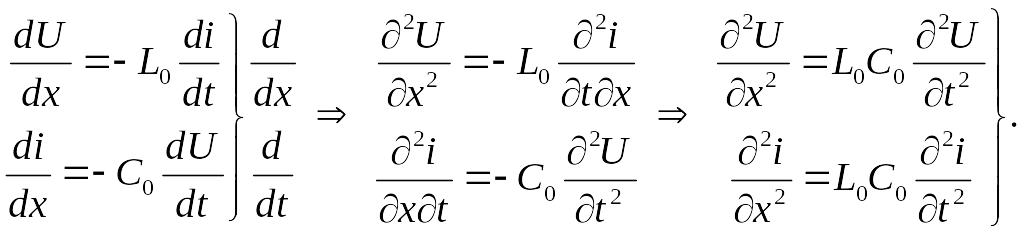
Полученные (крайние справа) уравнения для линии без потерь называются волновыми.
Уравнение, полученное аналогично, но с учетом R и G, для линий с потерями, называются телеграфными. Они записываются так
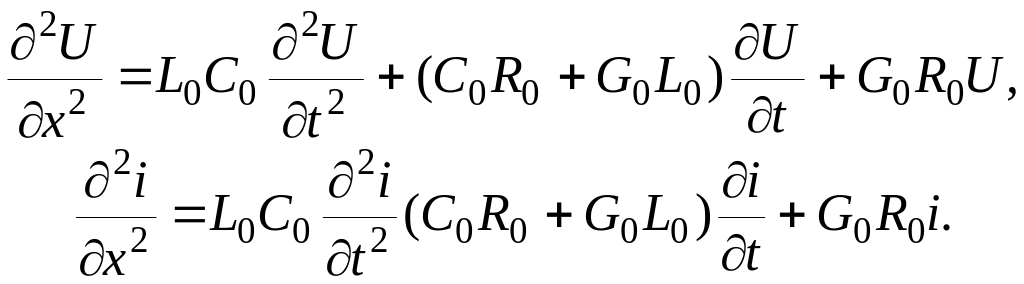
В общем случае решение волновых уравнений можно представить выражениями:
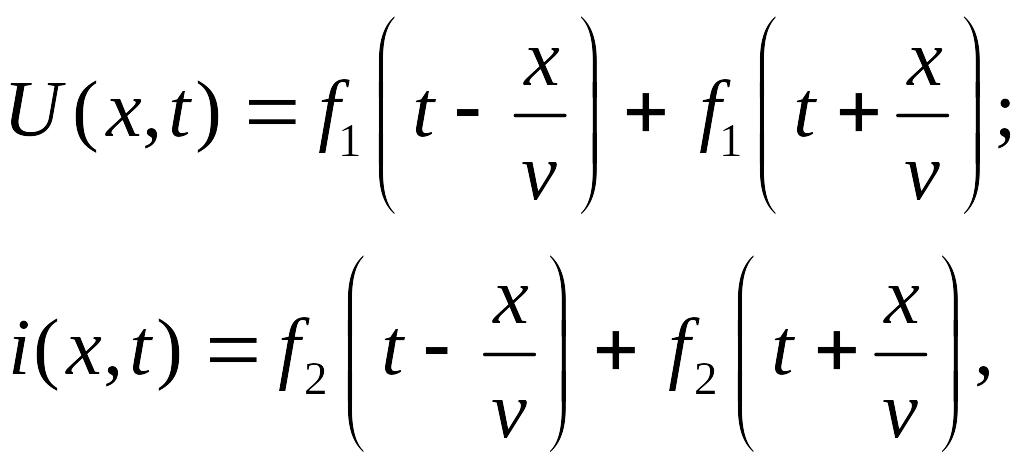
г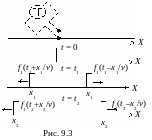 де
де
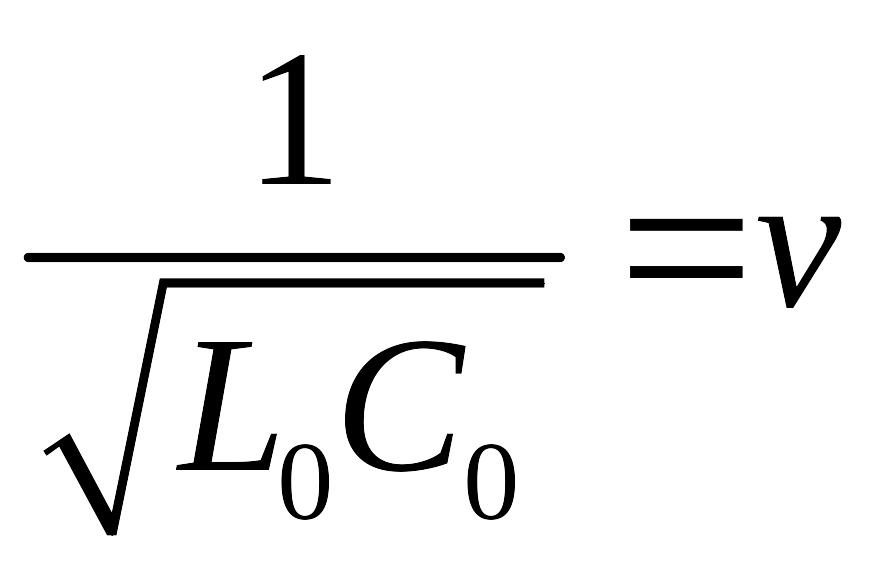 ,
функции f1
и f2
зависят от начальных и граничных условий,
т.е. от сигналов, которые подводятся к
длинной линии, но главное, эти функции
должны быть дважды дифференцируемыми.
,
функции f1
и f2
зависят от начальных и граничных условий,
т.е. от сигналов, которые подводятся к
длинной линии, но главное, эти функции
должны быть дважды дифференцируемыми.
Первое слагаемое называется прямой волной, а второе – обратной волной. С физической точки зрения, прямая волна характеризует сигнал, который распространяется в направлении х, а обратная волна – сигнал, который распространяется вдоль линии в противоположном направлении (рис. 9.3).
Вопрос 70-72
Электромагнитные волны распространяются с конечной скоростью. Это придает процессам, происходящим в электрических цепях, волновой характер, т.е. токи и напряжения в электрической цепи оказываются зависящими не только от времени t, но и от координаты сечения цепи x, т.е. U(x,t); i(x,t).
Если >>L, то участки цепи, состоят из элементов, обладающих только одним свойством и называются цепями с сосредоточенными параметрами, где = сТ = с/f – длина электромагнитной волны. Это расстояние между двумя точками, фазы колебаний в которых отличаются на 2π. Здесь с – скорость распространения волны; Т – период; f – частота; l – геометрический размер цепи. Все магнитные поля сосредоточены в катушках (L), все электрические поля – в конденсаторах (C), а потери – в резисторах (R).
Если <l, то в цепи невозможно выделить участок, обладающий одним свойством. Каждый участок цепи обладает одновременно свойствами R, L, C-элементов, т.е. параметры элементов как бы распределены по всему участку цепи. Такие цепи называют цепями с распределенными параметрами.
На частоте f = 1 кГц цепь длины l = 30÷40 км является цепью с распределенными параметрами. А на частоте f = 1 ГГц цепь длиной l = 2÷3 мм также является цепью с распределенными параметрами.
Примерами цепей с распределенными параметрами являются:
- воздушно-двухпроводная линия;
- электрический кабель;
- коаксиальный кабель;
- полосковая линия, прямоугольный или круглый волновод и т.д.
Цепи с распределенными параметрами часто называют длинными линиями.
