Вопрос 58

В основе операторного метода лежит преобразование Лапласа и операционное исчисление, известные из курса высшей математики. Операторный метод позволяет производить анализ переходных процессов при воздействии сигналов любой формы и не требует определения постоянных интегрирования, что существенно упрощает анализ электрических цепей, порядок которых выше чем первый.

Сущность операторного метода заключается в том, что функции  вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

Изображение  заданной функции  определяется в соответствии с прямым преобразованием Лапласа:

.

(1)

В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

или

.

Следует отметить, что если оригинал  увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

Вопрос 59-62

Электрические цепи служат для связи различных устройств между собой, при этом обычно ставится задача неискаженной передачи сигнала. В ряде случаев электрические цепи применяют для преобразования сигналов одной формы в другую.

Передача импульсных сигналов через дифференцирующую цепь

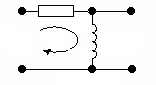
Цепь, состоящая из RC-элементов и приведенная на рис. 6.10, называется дифференцирующей RC-цепью.

Установим связь между выходным u₂ и входным u₁ напряжениями, считая входной сигнал u₁ произвольным.

Используя второй закон Кирхгофа и соотношения, устанавливающие связь между напряжениями и токами на элементах схемы, запишем

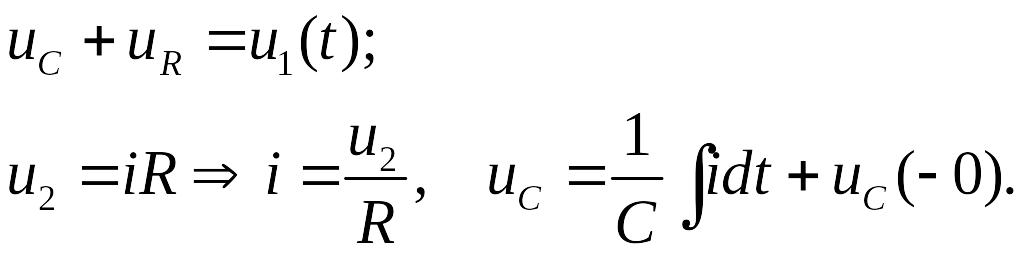
Считаем U_C(0).

Подставим полученные напряжения в первое выражение, умножим на RC и продифференцируем один раз по времени

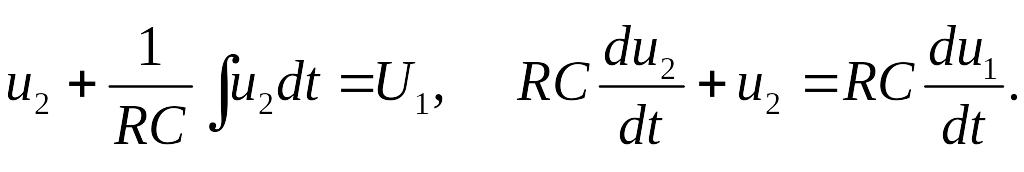
Если в этом соотношении считать, что . Последнее означает, что выходной сигнал есть производная от входного сигнала. Отсюда и название этой цепи – дифференцирующая цепь.

Рассмотрим два частных случая.

А. Пусть входной сигнал – ступенчатое напряжение амплитудой Е (рис. 6.11) . Используя классический метод, определим отклик цепи.

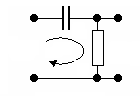
Рис. 6.10 Рис. 6.11

1) Составим дифференциальное уравнение и приведем его к стандартному виду:

.

2) Запишем общее решение

.

3) Найдем вынужденную составляющую общего решения

.

Вынужденную составляющую находим в стационарном (установившемся) режиме, который имеет место, когда t  ∞. В этом случае входной сигнал – постоянное напряжение величины , ему соответствует гармонический сигнал с нулевой частотой ω = 0, так как E = E cos ωt|_(ω=0). При таких условиях наличие индуктивности равносильно короткому замыканию (Х_L = ωL), а емкости – разрыву цепи (Х_С = (ωС)^–1).

Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω = 0 (рис. 6.12, а). Из схемы следует, что u_2(ω=0)= 0.

C

C

R

R

E

E

u_2() = 0

u₂₍₀₎ = E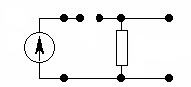

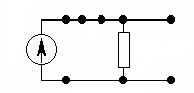
а б Рис. 6.12

4) Найдем показатель экспоненты р₁.

Коэффициенты р находят, как корни характеристического уравнения

RCр₁ + 1 = 0. Отсюда р₁ = – (RC)^–1.

5) Найдем произвольную постоянную A₁.

Произвольные постоянные находят из начальных условий для искомой функции и ее производных (при t = +0). Значения токов и напряжений в начальный момент времени после коммутации (при t = +0) определяют из схемы замещения исходной цепи, образованной после коммутации (с учетом законов коммутации) по законам Кирхгофа. При нулевых начальных условиях наличие индуктивности равносильно разрыву цепи (i_L(–0) = i_L(+0)), а емкости – короткому замыканию (u_c(–0) = u_c(+0)).

Аналогичную схему замещения можно получить, если считать, что ступенчатому сигналу в начальный момент времени (t = +0) соответствует гармонический с бесконечно большой частотой (ω  ∞).

Для дифференцирующей RC-цепи послекоммутационная схема (при t = +0, ω  ∞) приведена на рис. 6.12, б, а произвольную постоянную A₁ находят из уравнения

=A₁= .

6) Запись общего решения: .

Выходное напряжение представляет собой экспоненциальный импульс, который характеризуется двумя параметрами (рис. 6.13):

Рис. 6.13

1) Е – амплитуда импульса;

2) τ – постоянная времени цепи. Определим выходной сигнал при t = τ.

.

Отсюда следует, что постоянная времени – это время, за которое импульс, убывая по экспоненциальному закону, изменяется от Е до уровня 0,37Е (т.е. убывает в е = 2,71 раза).

Иногда пользуются третьим параметром: t_уст – время установления выходного напряжения, это время, за которое сигнал достигает своего стационарного значения с заданной точностью от амплитуды импульса. Так, время установления на уровне 0,1 и 0,05 составляет t_уст 0,1 = 2,3τ; t_уст 0,05 = 3τ.

Б. Пусть входной сигнал – одиночный прямоугольный импульс (рис. 6.14) амплитудой Е и длительностью t_и. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как .

Зная отклик на ступенчатый сигнал и используя принцип суперпозиции, можно записать аналитическое выражение для выходного сигнала: . На рис 6.15 показаны три временные диаграммы выходного сигнала при различных соотношения между τ и t_и.

E

u₁

t

E

E

E

–E

–E

–E

t

t

t

u₁

u₁

u₁

u₂

u₂

u₂

t_и

t_и

t_и

<< t_и

 >>t_и

 ~ t_и

а

б

в

t_и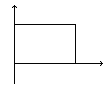

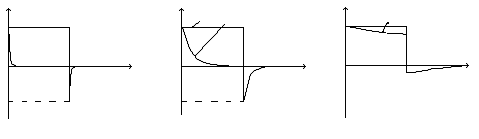
Рис. 6.14 Рис. 6.15

В зависимости от соотношения между τ и t_и эта схема имеет три названия.

Если τ << t_и, то цепь называется дифференцирующей RC-цепью (рис. 6.15, а). Если τ ≈ t_и, то цепь называется укорачивающей RC-цепью (рис. 6.15, б).Если τ >> t_и, то цепь называется разделительной RC-цепью (рис. 6.16, в).Рассмотрим процессы, протекающие в цепи при воздействии на вход прямоугольного импульса при нулевых начальных условиях u_c(–0) = 0.

Напряжения на элементах связаны вторым законом Кирхгофа u₁ = u_c + u_R.

При t < 0 u₁ = 0, u_c = 0, следовательно, u_R = 0. Это исходное состояние.

При t = +0 u₁ = Е, u_c = 0, E = 0 + u_R. Следовательно, u_R = Е. Это – послекоммутационное состояние цепи. При t > 0 E = u_c + u_R. Происходит заряд конденсатора.

С током i_зар заряда напряжение на нем возрастает, а на резисторе (на выходе) убывает от Е к нулю. При t = t_и–0 E = u_C(tи),+ u_R(tи),. К моменту окончания импульса u_c = u_c(tи), u_R = Е – u_c(tи).

При t > t_и+0 u₁ = 0 = u_c + u_R.. Следовательно, u_R = –u_c. Поэтому знак выходного напряжения меняется на противоположный.

u1(t) i(t) R L u2(t)

Рис. 6.16

При t > t_и u₁ = 0 , u_R = –u_c. Происходит разряд конденсатора С током i_разр разряда, напряжение на нем убывает, убывает и напряжение на резисторе (на выходе) от –u_c(tи) к нулю.

Цепь, состоящая из RL-элементов (рис 6.16), выполняет аналогичные преобразования над входными сигналами и называется дифференцирующей RL-цепью.