4. Комплексная мощность. Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,    .

 где  - комплекс, сопряженный с комплексом .

Среднее значение мгновенной мощности (активная мощность) Р_A:

Р_А = UI cos(_u – _i);

φ = _u – _i – фазовый сдвиг между током и напряжением.

р_А - максимальна, когда ток и напряжение находятся в одной фазе φ = 0, т.е. _u = _i.

Активная мощность выделяется (поглощается) на участке цепи, совершая полезную работу, превращаясь в тепловую или механическую форму энергии.

Активная мощность измеряется в ваттах (Вт).

2. Реактивная мощность

P_Q = UI sin(_u – _i).

P_Q характеризует энергию, которая накапливается реактивными элементами цепи и возвращается затем в цепь. P_Q иногда называют «кажущаяся» мощность т.к., она P_Q не потребляется участком цепи и не выполняет никакой работы.

Реактивная мощность измеряется в варах (Вар – вольт-ампер реактивный).

Вопрос 37

электрическая мощность P (t), выделяющаяся на элементе электрической цепи — произведение мгновенных значений напряжения U (t) и силы тока I (t) на этом элементе:

Если элемент цепи — резистор c электрическим сопротивлением R, то

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам:

Мощность переменного тока

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Вопрос 38 Параметры двухполюсника

Двухполюсником является цепь с двумя выводами рис. 5.2. Его режим работы характеризуется двумя величинами

1. Если воздействием считать амплитуду тока, то откликом будет являться напряжение на нем.

По закону Ома: , где Z – сопротивление двухполюсника. (Z = R+jX – комплексное число, где R и X – резистивная и реактивная составляющие сопротивления двухполюсника).

Обобщенная схема замещения двухполюсника приведена на рис. 5.3.

2. Если воздействием считаем амплитуду напряжения, тогда откликом будет амплитуда тока, связанная с напряжением:

; ,

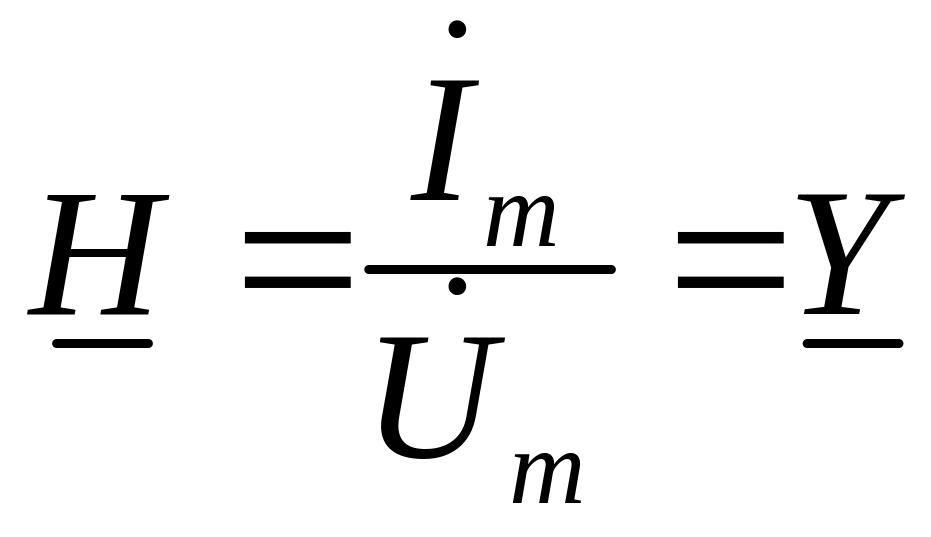г де Y – второй параметр двухполюсника, он называется комплексной проводимостью двухполюсника:

Y = G + jB,

G и B – резистивная и реактивная составляющие проводимости двухполюсника.

Вторая схема замещения двухполюсника приведена на рис. 5.4. Эти схемы замещения при определенном выборе параметров эквивалентны.

Вопрос 39

Под частотными характеристиками (ЧХ) понимают следующие типы характеристик:

1. Зависимость модуля входного сопротивления (проводимости) от частоты ω.

2. Зависимость действительной или мнимой части входного сопротивления (проводимости) от частоты ω.

ЧХ могут быть получены расчетным (если известна схема, характер элементов и их числовые значения), либо опытным путем (в этом случае схему двухполюсника и характер её элементов знать не обязательно).

При снятии ЧХ опытным путём на вход двухполюсника подают напряжение, частоту которого изменяют в широких пределах, начиная с нуля, и по результатам измерений подсчитывают модуль входного сопротивления (проводимости) или действительную (мнимую) часть входного сопротивления (проводимости).

В общем случае двухполюсники содержат резистивные и реактивные элементы. В частном случае двухполюсники могут состоять из реактивных элементов, тогда их называют реактивными двухполюсниками. Применительно к ним под ЧХ понимают зависимости или . ЧХ для несложных двухполюсников, содержащих резистивные и реактивные элементы, иногда можно качественно строить на основании простых физических изображений о характере изменения сопротивления отдельных элементов этого двухполюсника при изменении частоты. Если это сделать затруднительно, то прибегают к аналитическому расчету, либо к снятию ЧХ опытным путём.