
- •Вопрос №1
- •Вопрос №2
- •Вопрос №4
- •Вопрос №6
- •Вопрос №7
- •Вопрос №8
- •Вопрос №9
- •Вопрос №10
- •Вопрос 11
- •Вопрос12
- •Вопрос №13
- •Вопрос №14
- •Вопрос №15
- •Вопрос №16
- •Вопрос 18
- •Вопрос №17
- •Вопрос №19
- •Вопрос №20
- •Вопрос №21
- •Эквивалентное преобразование источников электрических сигналов
- •Вопрос 22
- •Вопрос23
- •Вопрос24
- •Вопрос №25
- •Вопрос №26
- •Вопрос №27
- •Вопрос №28
- •Вопрос №29
- •Вопрос №30
- •Вопрос №31
- •Вопрос №32
- •Вопрос №34
- •2. Законы Кирхгофа в комплексной форме.
- •Вопрос 35
- •Вопрос 36
- •4. Комплексная мощность. Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
- •Вопрос 37
- •Вопрос 38 Параметры двухполюсника
- •Вопрос 39
- •Вопрос 40 Параметры четырехполюсника
- •Вопрос 41 Частотные характеристики четырехполюсников
- •Вопрос 42
- •Вопрос 43 Последовательный колебательный контур состоит из последовательного соединения индуктивности l и емкости c (рис. 5.17).
- •Вопрос 49
- •Спектральный метод анализа
- •Основные определения нелинейных цепей
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Вопрос 53
- •Вопрос 54
- •Классический метод анализа
- •Спектральный метод анализа
- •Вопрос 55
- •Вопрос 56 Метод интеграла Дюамеля
- •Вопрос 58
- •Вопрос 59-62
- •Передача импульсных сигналов через дифференцирующую цепь
- •Передача импульсных сигналов через интегрирующую цепь
- •Вопрос 63-65
- •Вопрос 66
- •Вопрос 67
- •Схемы замещения по заданной топологии
- •Формальные схемы замещения
- •Вопрос 68
- •Основные понятия для идеальных фильтров
- •Классификация фильтров электрических сигналов
- •Вопрос 69
- •Понятие о длинной линии и распространение волн в ней
- •Вопрос 70-72
- •Понятие о длинной линии и распространение волн в ней
- •Полубесконечная длинная линия
- •Линия конечной длины. Отражения
- •Режимы работы длинной линии
- •Коэффициент бегущей волны и коэффициент стоячей волны
- •Применение длинных линий
Вопрос 42

Индуктивность L - величина, равная отношению потокосцепления, связанного с контуром, к силе тока, протекающего по нему:
Индуктивность складывается из внутренней индуктивности (жилы кабеля и провода) L в и наружной, междужильной, индуктивности L и
Единица индуктивности генри (гн) - индуктивность контура, с которым сцеплен магнитный поток 1 вб, когда по контуру течет ток 1 а, или индуктивность контура, в котором возникает э. д. с. самоиндукции 1 в при изменении тока в нем на 1 а в 1
Вопрос 43 Последовательный колебательный контур состоит из последовательного соединения индуктивности l и емкости c (рис. 5.17).
Для
анализа процессов, протекающих в контуре,
воспользуемся эквивалентной схемой
замещения контура, в которой учтем
резистивные сопротивления потерь
реальных реактивных элементов (рис.
5.18). Здесь RL
– резистивное сопротивление провода
катушки индуктивности, Rут
– сопротивление утечки диэлектрика
конденсатора, RC
– сопротивление утечки, пересчитанное
в последовательную ветвь. Схема замещения
последовательного контура приведена
на рис. 5.19. В ней
![]() – резистивное сопротивление контура,
учитывает резистивные сопротивления
реактивных элементов. Определим частотную
характеристику входного сопротивления
последовательного колебательного
контура:
– резистивное сопротивление контура,
учитывает резистивные сопротивления
реактивных элементов. Определим частотную
характеристику входного сопротивления
последовательного колебательного
контура:
![]() ,
где R
и
,
где R
и
![]() – резистивная и реактивная составляющая
сопротивления последовательного
колебательного контура;
– резистивная и реактивная составляющая
сопротивления последовательного
колебательного контура;
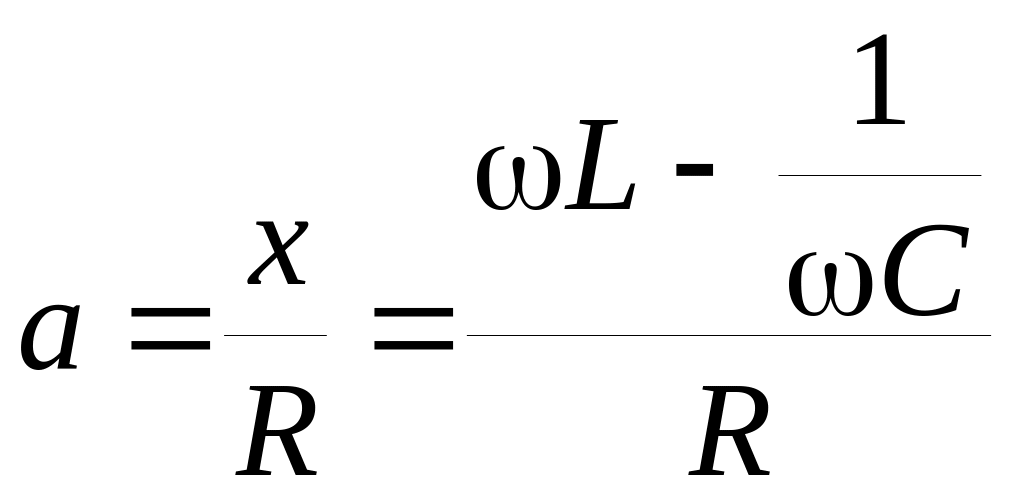 –
обобщенная
расстройка колебательного контура.
–
обобщенная
расстройка колебательного контура.
Ч астота,
на которой выполняется это условие,
называется резонансной, она определятся
как ω0 =
(LC)–1/2
.
астота,
на которой выполняется это условие,
называется резонансной, она определятся
как ω0 =
(LC)–1/2
.
Отметим свойства последовательного контура на резонансной частоте:
1)
![]() сопротивление имеет резистивный характер
и минимально по сравнению с сопротивлением
на других частотах.
сопротивление имеет резистивный характер
и минимально по сравнению с сопротивлением
на других частотах.
2)
Начальные фазы напряжения и тока на
контуре одинаковы φu
= φi,
сдвиг по фазе равен φ = φu
– φi
= 0. 3) Амплитуда тока в контуре максимальна
и равна
![]() .
.
4)
Сопротивления реактивных элементов L
и C одинаковы и равны
![]() –
характеристическому сопротивлению
контура, т.е.
–
характеристическому сопротивлению
контура, т.е.
![]() .
5)
Амплитуды напряжений на реактивных
элементах контура одинаковы и в Q
(добротность) раз больше
.
5)
Амплитуды напряжений на реактивных
элементах контура одинаковы и в Q
(добротность) раз больше
![]() (амплитуды
напряжения на входе).
(амплитуды
напряжения на входе).
6)
Амплитуды напряжений на реактивных
элементах находятся в противофазах, а
поэтому суммарное напряжение на
реактивных элементах равно нулю:
![]() .
.
Резонансная характеристика последовательного колебательного контура
Это
есть зависимость от частоты отношения
комплексной амплитуде тока
к комплексной амплилитуде тока при
резонансной частоте, т.е.
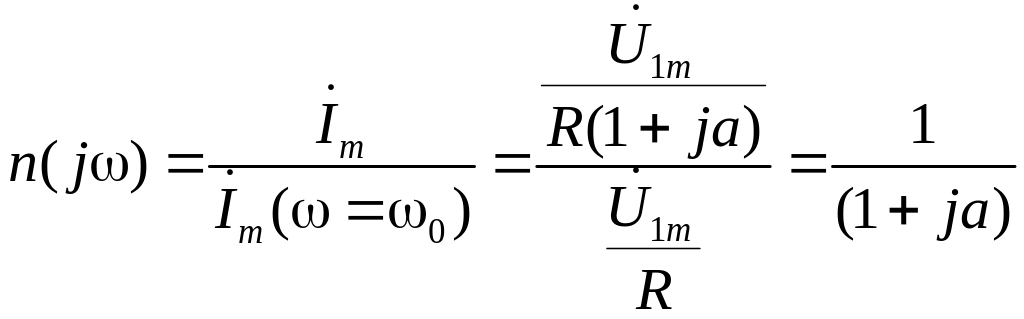 .
Важным параметром колебательного
контура является его полоса пропускания
(S). Это диапазон частот,
в котором резонансная характеристика
превышает уровень
.
Важным параметром колебательного
контура является его полоса пропускания
(S). Это диапазон частот,
в котором резонансная характеристика
превышает уровень
![]() ,
т.е.
,
т.е.
![]() ,
S = ωв
– ωн, где ωв, ωн –
верхняя и нижняя граничные частоты
полосы пропускания
,
S = ωв
– ωн, где ωв, ωн –
верхняя и нижняя граничные частоты
полосы пропускания
Вопрос 44

Вопрос 45


Вопрос 46


СОПРОТИВЛЕНИЯ нагрузки на избирательные свойства одиночного последовательного колебательного контура

Вопрос 47
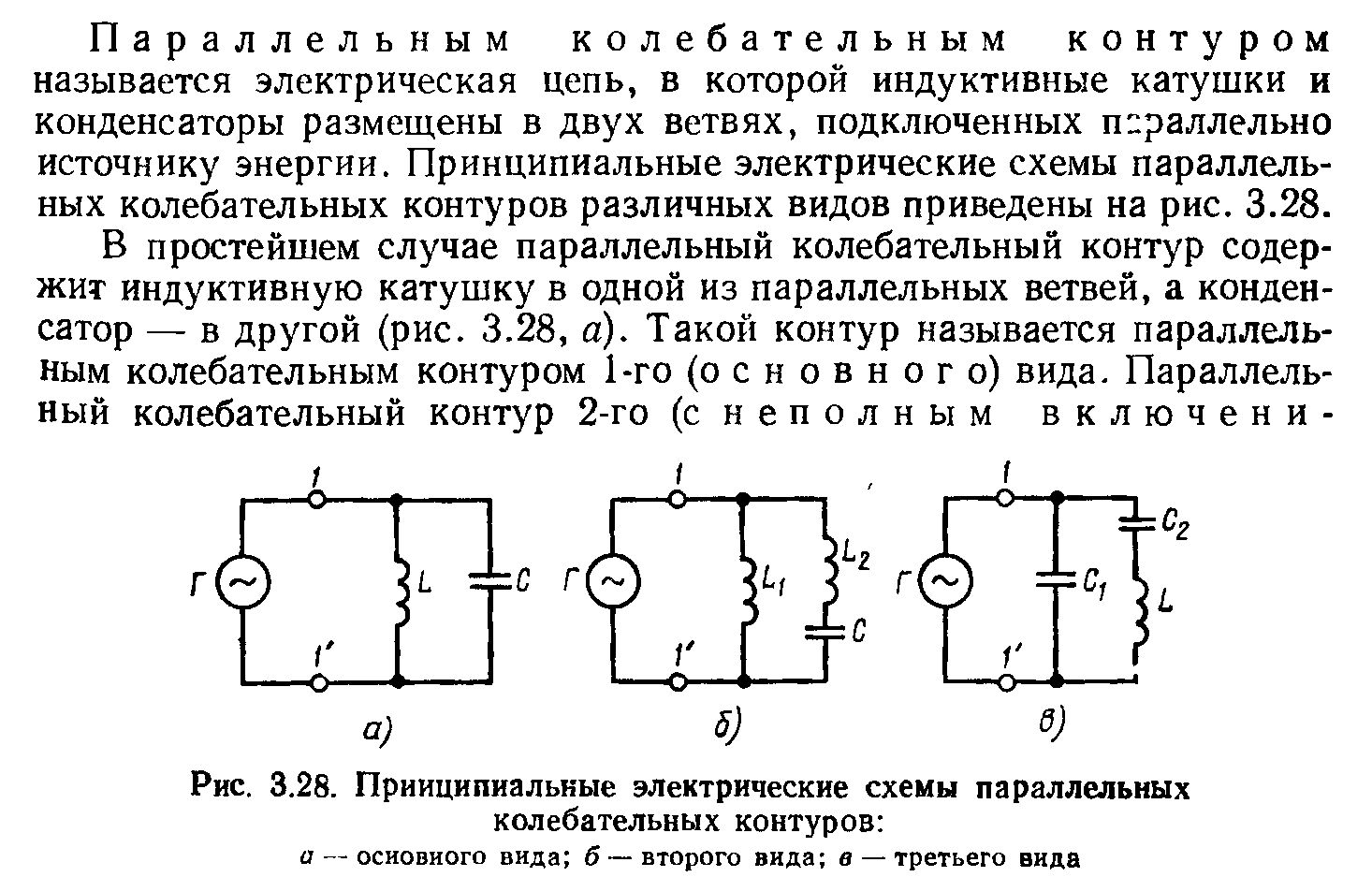
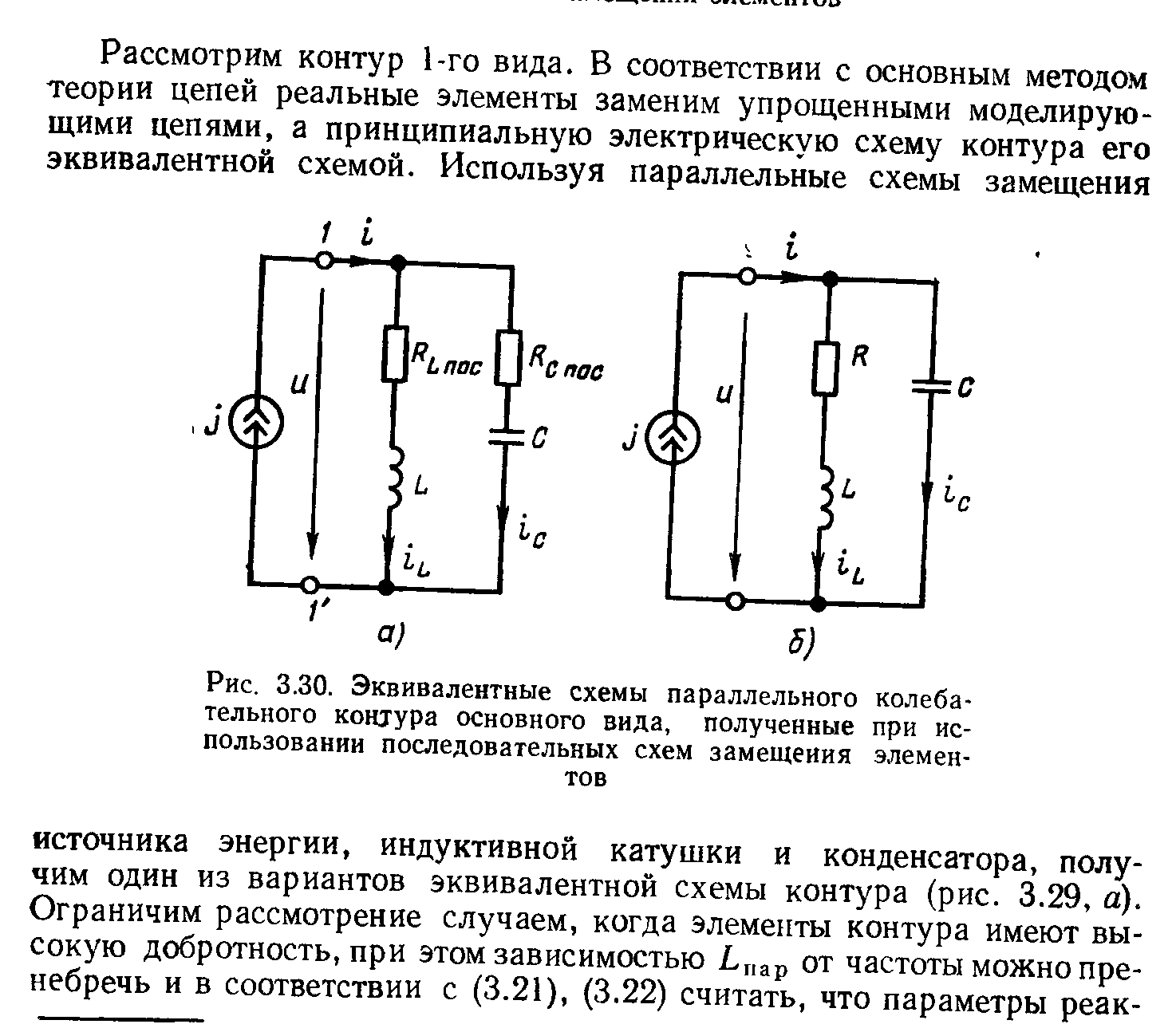

При
частоте входного сигнала равного
собственной частоте контура |xL|=|xC| и в
контуре наступает резонанс на частоте
равной
![]() .
.
Из выражения (3.59) видно, что при |xL|=|xC| с учетом, что Q= ρ/R сопротивление контура равно:
Zρ=ρ2/R=Qρ (3.60)
При резонансе ток в контуре определяется выражением Ik=U/ρ. Учитывая, что U=Iг ZP и учитывая выражение (3.60) будем иметь:
Ik=Iг ZP/ρ=Iг Q (3.61)
Из (3.61) видно, что при ω=ω0 ток в контуре превышает ток входного генератора в Q раз. Такое явление называют резонансом тока.
Частотные характеристики параллельного контура без потерь определяются зависимостью параметров его элементов от частоты и имеют вид:
![]()
![]()
![]() (3.62)
(3.62)
Графики частотных зависимостей (3.62) изображены на рис.3.11
Р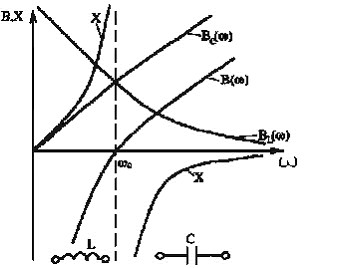 ис.
3.11. Частотные характеристики параллельного
колебательного контура.
ис.
3.11. Частотные характеристики параллельного
колебательного контура.
Из рисунка видно, что при ω<ω0 входное сопротивление контура носит индуктивный характер, а при ω>ω0 – емкостной характер. На резонансной частоте ω=ω0 вследствие отсутствия потерь входное реактивное сопротивление контура претерпевает разрыв (|Х|= ∞).
Согласно Закону Ома токи в ветвях контура определяются формулами:
![]()
![]() (3.63)
(3.63)
Анализ (3.63) показывает, что с увеличением частоты ω ток I1(ω) уменьшается, а I2 растет. При ω=∞ токи становятся равными I1(∞)=0; I2(∞)=U/R. Если контур подключен к источнику с напряжением Uг и внутренним сопротивлением Rг, то комплексное напряжение на контуре определяется уравнением:
.
![]() (3.64) где Z определятся (3.59). На
резонансной частоте ξ=0, поэтому (3.64) с
учетом (3.59) примет вид:
(3.64) где Z определятся (3.59). На
резонансной частоте ξ=0, поэтому (3.64) с
учетом (3.59) примет вид:
![]() (3.65)
(3.65)
Определим частотную зависимость Uk/Uk(p) . Учитывая (3.64-3.65) и (3.59) будем иметь:
![]() (3.66) АЧХ контура
зависит от внутреннего сопротивления
генератора Rг. Вид АЧХ (3.69) для двух
значений Rг приведена на рис.3.12:
(3.66) АЧХ контура
зависит от внутреннего сопротивления
генератора Rг. Вид АЧХ (3.69) для двух
значений Rг приведена на рис.3.12:
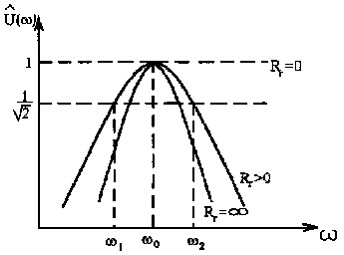
Рис. 3.12. АЧХ параллельного колебательного контура.
Ширину полосы пропускания контура определим как диапазон частот, на границе которого напряжение на контуре уменьшается в раз относительно Uk(p).
![]()
Из этого уравнения получаем граничные частоты полосы пропускания:
![]() Отсюда
ширина полосы пропускания параллельного
колебательного контура равна:
Отсюда
ширина полосы пропускания параллельного
колебательного контура равна:
![]() (3.70)
(3.70)
Анализ выражения (3.70) показывает, что Δƒ зависит от величины внутреннего сопротивления генератора Rг и что только при Rг→ ∞ можно получить узкую полосу(см.рис.3.12). Отсюда следует, что для улучшения избирательных свойств параллельного контура (для уменьшения Δƒ) его необходимо возбуждать источником тока.
