Вопрос №28

Преобразование Фурье применяется лишь для сигналов с конечной энергией, т. е. для сигналов, удовлетворяющих условию .

Функция s(t), удовлетворяющая записанному условию, называется абсолютно интегрируемой. Более универсальным является операторное представление сигнала, которое основано на преобразовании Лапласа. При операторном представлении сигналу s(t), как функции действительной переменной t, ставится в соответствие функция комплексной переменной р – S(p), где p = σ + jω (p называется комплексной частотой). Эта функция вводится следующим выражением:

– прямое преобразование Лапласа (ППЛ), (S(p) = L[s(t)]);

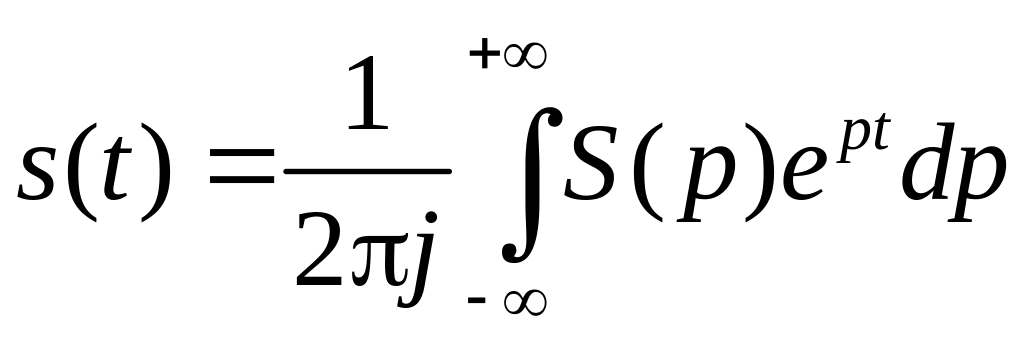– обратное преобразование Лапласа (ОПЛ), (s(t) = L^–1 [S(p)]).

Сигнал s(t) называют оригиналом, а S(p) – изображением, или операторным представлением сигнала.

Д ля нахождения функции спектральной плотности S(jω) по известному операторному представлению S(p) сигнала необходимо оператор р заменить на jω, т.е. S(jω) = S(р)|_{р = jω} . Пример. Найти спектральную плотность S(jω) для единичной функции (рис. 2.15).

;

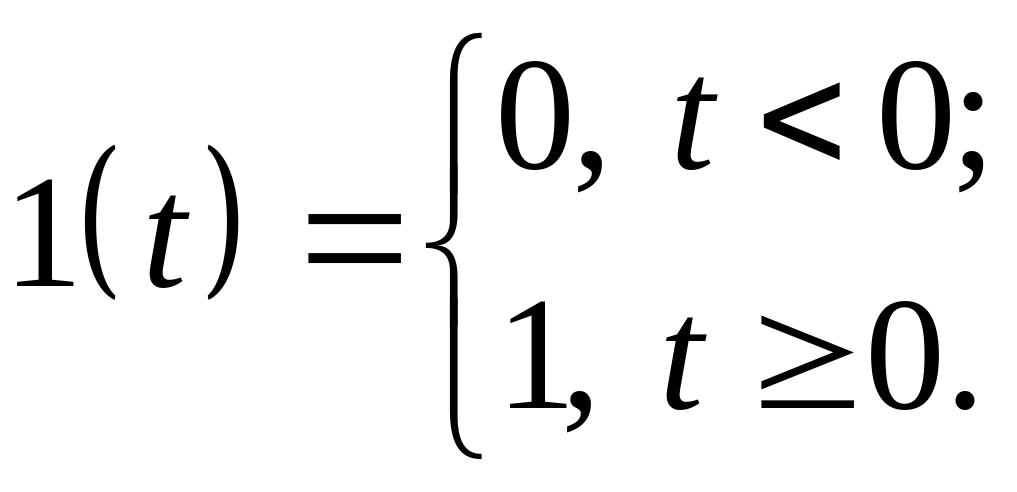
1) Спектр суммы сигналов равен сумме спектров этих сигналов, т.е.

S₁(t)  S₁(jω); S₂(t)  S₂(jω); S(t) = S₁(t)+S₂(t)  S(jω) = S₁(jω) + S₂(jω).

Э то вытекает из свойства линейности преобразования Фурье. 2) Спектр сигнала, сдвинутый по оси времени на время t_з (время задержки), равен спектру исходного сигнала, помноженного на множитель , т.е. если S₁(t) S(jω), то S₂(t) = S₁(t – t_з)  S₁(jω) . На рис. 2.16 приведены сигналы: без временного сдвига (рис. 2.16, а), сигнал с задержкой на время t₀ (рис. 2.16, б) и сигнал с опережением на время t₀ (рис. 2.16, в). 3) Изменение масштаба сигнала по оси времени приводит к изменению масштаба его спектра по оси частот

s₁(t)  S₁(jω); s₂(t) = S₁(αt); s₂(t) = S₁(jω /α).

Если α > 1, то сигнал сжимается по оси времени, что приводит к растяжению его спектра по оси частот. Если 0 < α <1, то сигнал растягивается по оси времени, а его спектр сжимается по оси частот.

Вопрос №29

1) Спектр суммы сигналов равен сумме спектров этих сигналов, т.е.

S₁(t)  S₁(jω); S₂(t)  S₂(jω); S(t) = S₁(t)+S₂(t)  S(jω) = S₁(jω) + S₂(jω).

Это вытекает из свойства линейности преобразования Фурье.

2) Спектр сигнала, сдвинутый по оси времени на время t_з (время задержки), равен спектру исходного сигнала, помноженного на множитель , т.е. если S₁(t) S(jω), то S₂(t) = S₁(t – t_з)  S₁(jω) .

3) Изменение масштаба сигнала по оси времени приводит к изменению масштаба его спектра по оси частот

s₁(t)  S₁(jω); s₂(t) = S₁(αt); s₂(t) = S₁(jω /α).

Если α > 1, то сигнал сжимается по оси времени, что приводит к растяжению его спектра по оси частот.

Если 0 < α <1, то сигнал растягивается по оси времени, а его спектр сжимается по оси частот.

Пример: s₁(t) = cos ωt; s₂(t) = cos 2ωt.

4) Дифференцирование сигнала эквивалентно умножению его спектра на множитель jω.

Пусть сигнал s₁(t) имеет спектральную плотность S₁(jω), (s₁(t) → S₁(jω)), тогда s₂(t) = d (S₁(t))dt; S₂(j) = j S₁(jω).

При дифференцировании выделяются высокочастотные составляющие спектра сигнала, а низкочастотные ослабляются, так как имеют малый масш-табный множитель.

5) Интегрирование сигнала эквивалентно умножению спектра на множитель 1/jω.

Пусть сигнал s₁(t) имеет спектр S₁(j), (s₁(t)  S₁(jω)), тогда

s₂(t) =  s₁(t) dt; S₂(j) = (1/j) S₁(jω)).

При интегрировании выделяются низкочастотные составляющие, а высокочастотные подавляются.