28. Применение метода редукции для решения краевой задачи на основе оду-2.

Рассмотрим метод редукции для двухточечной краевой задачи на основе ОДУ второго порядка.

(8)

(9)

(10)

где p(x),q(x),f(x) – известные функции, определенные на отрезке поиска решения, а параметры имеют конкретное числовое значение, причем выполняется условие .

Ищем общее решение в виде

(11)

Далее необходимо решить три задачи Коши

(12)

(13)

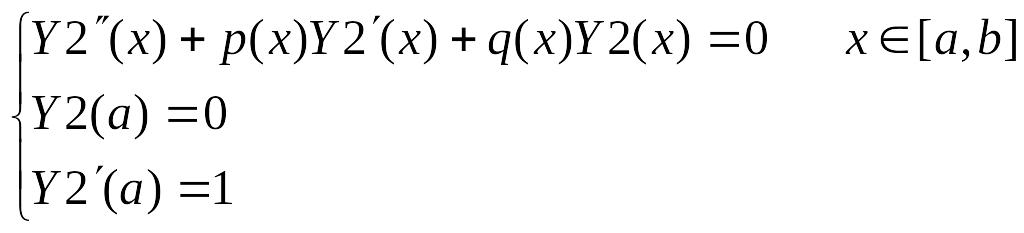(14)

Решив эти системы (12)-(14) численным методом, получим в узлах выбранной сетки, в том числе на правом конце отрезка, значения функций Y0,Y1,Y2. Подставим эти найденные значения в краевые условия

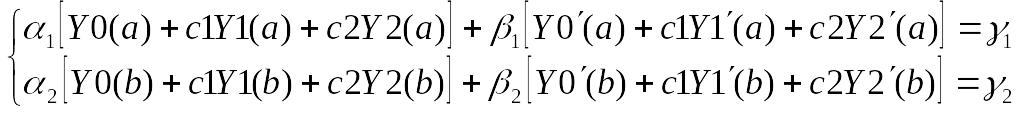(15)

Учтем из (12)-(14), что

Y0(a)=0, , Y1(a)=1, , Y2(a)=0, и получаем систему

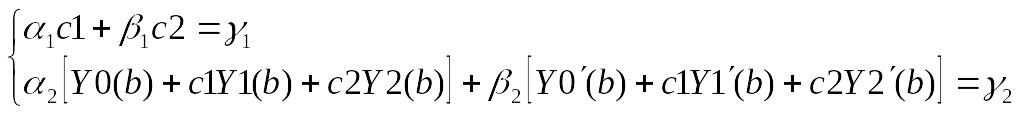(16)

Из системы (16) найдем значения коэффициентов c1, c2 и подставим их в соотношение (11), на основание которого можем найти искомое решение в любой точке отрезка поиска решения.

29. Решение краевой задачи методом стрельбы. Геометрическая интерпретация.

Суть этого метода заключается в сведении решения краевой задачи к многократному решению задач Коши. Принцип построения метода стрельбы рассмотрим, упростив задачу (1)-(3). Будем предполагать, что отрезок поиска решения задачи [0,1]. Известно, что любой отрезок [a,b] можно заменить отрезком [0,1], путем ввода замены переменной вида 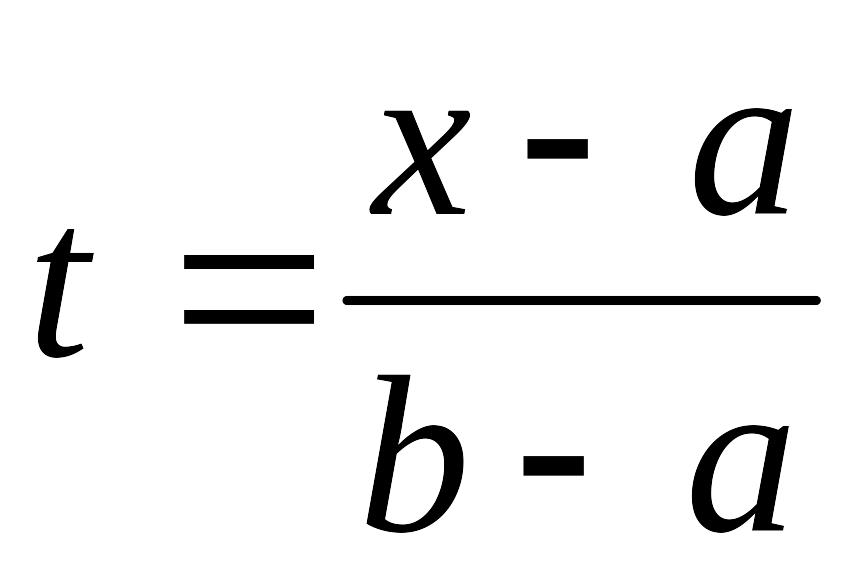(4) Граничные условия на концах рассматриваемого отрезка также примем в простейшем виде, т.е. u(0)y(0)=Y0 , u(1) y(1)=Y1 (5)

П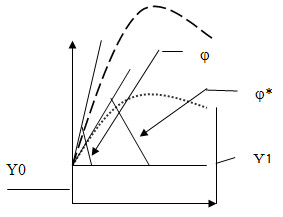 онизим порядок уравнения (1) и запишем его в виде задачи Коши с начальными условиями 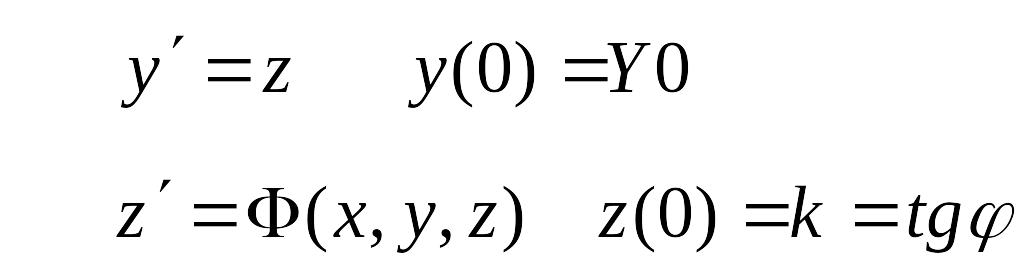(6) Y0 - это точка на оси ординат, в которую помещается начало искомой интегральной кривой, - угол наклона касательной к интегральной кривой в этой точке. Угол наклона  в процессе многократного решения краевой задачи должен принять такое значение, чтобы интегральная кривая «попала в цель», т.е. в точку (1,Y1).

Считаем решение задачи Коши (6) зависящим от параметра . Будем искать такую интегральную кривую , которая выходит из точки (0,Y0) и попадает в точку (1,Y1). Т.о. если =*, то решение задачи Коши (6) y(x) совпадает с решением u(x)  y(x) краевой задачи (1),(5). Тогда, если x=1, то учитывая второе граничное условие (5), получаем y(1, )=Y1 или y(1, ) - Y1=0 (7)

Следовательно, получили уравнение вида F()=0, где F()=y(1, )-Y1. Особенность этого уравнения заключается в том, что функцию F() нельзя представить в виде некоторого аналитического выражения, т.к. она является результатом численного решения (т.е. таблицей чисел) задачи Коши (1),(5). Тем не менее, для решения уравнения (7) можно использовать любой известный метод численного решения нелинейных уравнений. Например, метод деления отрезка пополам, метод секущих. В этом случае берем сначала отрезок [0, 1], содержащий *. К примеру, 0=0, 1=/2. На концах [0, 1] функция F() должна принимать значения разных знаков. Для этого решение задачи Коши y=y(x, 0) должно при x=1 располагаться ниже точки (1,Y1), т.е Y1y=y(1, 0), а y(1, 1)  Y1– выше. Далее, полагая 2=(0+1)/2, снова решаем задачу Коши при =2 и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков [0, 2] или [2, 1], на котором функция F() не меняет знак и т.д. Процесс поиска решения исходной задачи прекращается, если разность двух последовательно найденных значений  меньше заранее заданной точности . В этом случае последнее решение задачи Коши принимается за искомое решение исходной краевой задачи. При использовании метода секущих выбираем два начальных приближения и последующие значения находим по формуле Вычисления продолжают до тех пор, пока не выполнится условие , где  - заранее заданная точность.

Описанный алгоритм называется методом стрельбы, т.к. в нем как бы проводится «пристрелка» по углу наклона касательной к интегральной кривой в начальной точке. Точность решения краевой задачи зависит не только от точности определения параметра , но также от точности решения соответствующей задачи Коши. Поэтому одновременно с уточнением параметра  рекомендуется уменьшать шаг при решении задачи Коши, либо выбрать более точный метод. Алгоритм стрельбы хорошо работает в том случае, если решение не слишком чувствительно к изменениям параметра , иначе алгоритм может оказаться неустойчивым.