43. Приближённое вычисление интегралов.

Задача численного интегрирования состоит в том решить численными методами задачу 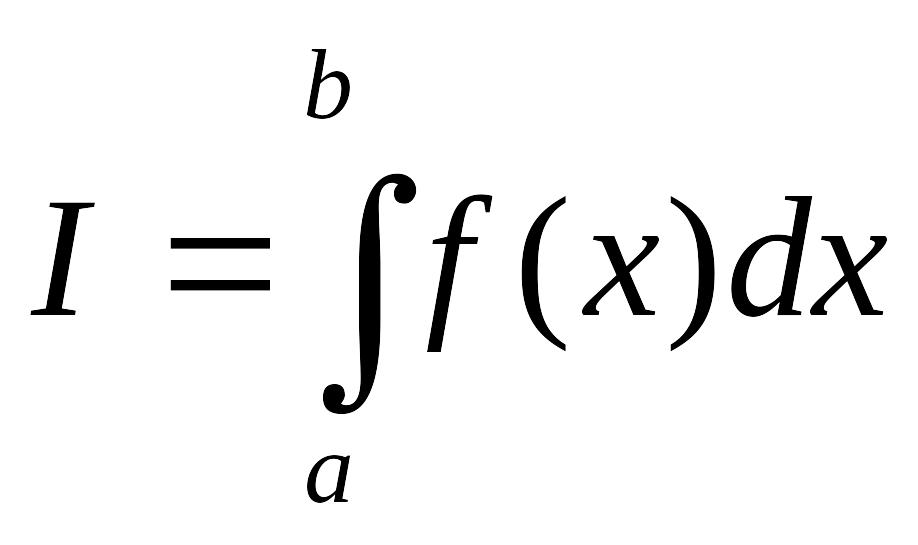(1) по формуле Ньютона-Лейбница 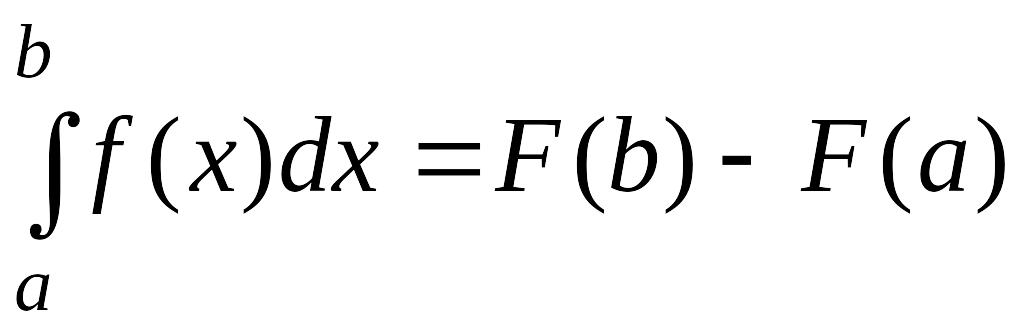(2)

Однако на практике не всегда удается применить формулу (2) по следующим причинам:

1. вид функции f(x) не допускает непосредственного интегрирования, т.е. первообразную невозможно выразить в элементарных функциях.

2. аналитическое выражение первообразной F(x) таково, что получить числовой ответ трудно из-за весьма сложных преобразований.

3. подынтегральная функция f(x) задана в виде графика или таблицы.

В этих случаях используют методы численного интегрирования, которые основаны на аппроксимации подынтегральной функции f(x) некоторой функцией, имеющей более простое аналитическое выражение, (например многочленом,) и интеграл от которой легко вычисляется аналитически. Одним из таких способов является представление подынтегральной функции f(x), если она задана аналитически, в виде степенного ряда Тейлора. Такой прием позволяет свести вычисление интеграла от сложной функции к интегрированию многочлена, представляющего первые несколько членов ряда.

Более универсальным методом является аппроксимация подынтегральной функции f(x) интерполяционным многочленом. Это позволяет приближенно заменить определенный интеграл некоторой конечной суммой, которую называют квадратурной. Эта сумма схожа с интегральной. Пусть на отрезке [a,b] задана непрерывная функция f(x). Разобьем этот отрезок на n элементарных отрезков точками . На каждом элементарном отрезке выберем произвольную точку и найдем произведение значения функции на длину этого отрезка , т.е. . Составим сумму таких произведений по всем элементарным отрезкам. 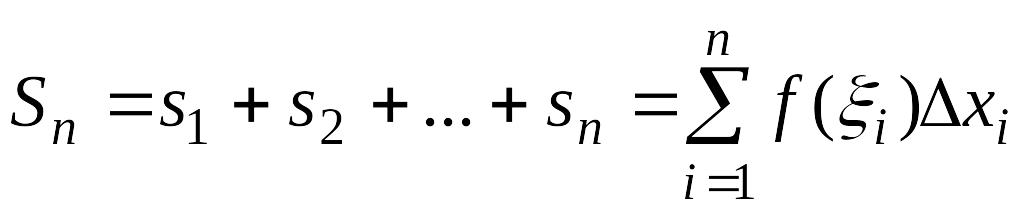(3)

Сумма называется интегральной суммой. Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения отрезка [a,b]. При этом длина наибольшего из элементарных отрезков стремится к нулю.

(4)

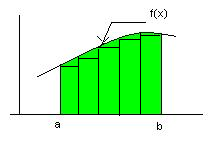
Геометрический смысл определенного интеграла для

f(x) >0: равен площ криволинейной трапеции, а интегральная сумма совпадает с площадью ступенчатой фигуры. Имеет место следующая теорема существования определенного интеграла. Если функция f(x )непрерывна на отрезке [a,b], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [a,b] на элементарные отрезки, ни от выбора точек .

Исходя из понятий интегральной суммы, определенного интеграла и теоремы о существовании определенного интеграла строятся простейшие формулы для приближенного вычисления интегралов по отрезку. Такие формулы называются квадратурными. В многомерных случаях, т.е когда размерность интеграла больше 1, формулы для приближенного вычисления определенного интеграла называются кубатурными.

В общем виде задачу нахождения определенного интеграла обычно формулируется следующим образом. Пусть для непрерывной на отрезке [a,b] функции f(x) требуется найти приближенное значение определенного интеграла вида

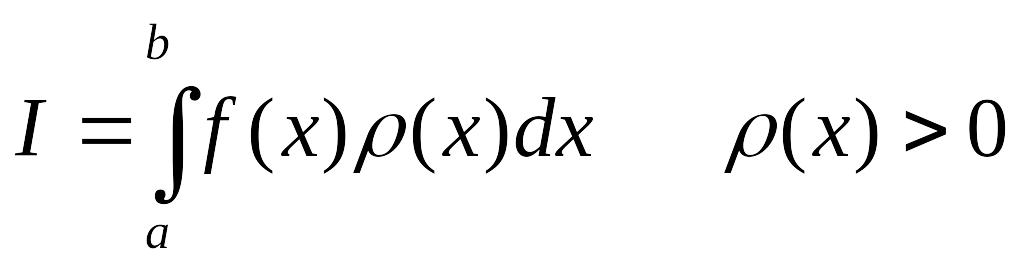(5)

Где весовая функция непрерывна на интервале (a,b). Выразить интеграл через элементарные функции удается редко, а компактный и удобный для доведения до числа ответ получается еще реже. Поэтому обычно заменяют f(x) на такую аппроксимирующую функцию (x,a), т. е. f(x) (x,a), ,a- вектор параметров, чтобы интеграл от нее легко вычислялся в элементарных функциях. Чаще всего подынтегральную функцию f(x) заменяют некоторым обобщенным интерполяционным многочленом. Поскольку такая аппроксимация является линейной относительно параметров, то функция при этом заменяется некоторым линейным выражением, коэффициентами которого являются значения функции в узлах.

(6)

- остаточный член аппроксимации. Подставим аппроксимацию (6) под знак интеграла (5), получим формулу численного интегрирования, т.е. квадратурную формулу

(7)

Где 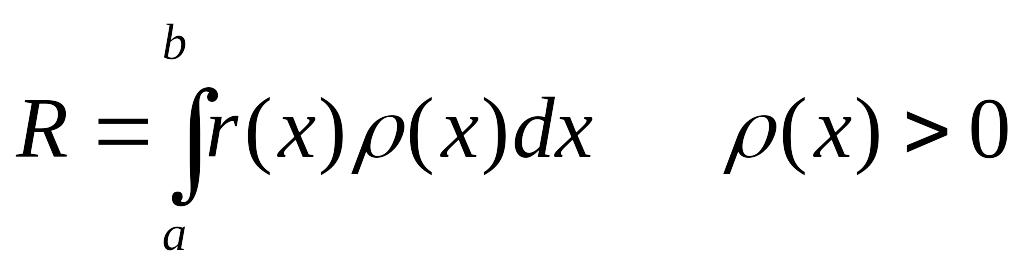. Величины называются узлами, - весами, а R – погрешностью ( или остаточным членом) квадратурной формулы. Параметры , не зависят от f(x). Весовая функция обычно полагают равной единице .

Таким образом, задача приближенного решения определенного интеграла (численного интегрирования) состоит в замене интеграла конечной суммой

(8)

Где - некоторые числовые коэффициенты, . Приближенное равенство (9)

Называется квадратурной формулой, правая часть этого равенства представляет собой квадратурную сумму. Точки - это узлы квадратурной формулы, - коэффициенты квадратурной формулы. Разность (10)

называется погрешностью квадратурной формулы. Очевидно, что погрешность квадратурной формулы зависит как от расположения узлов , так и от выбора коэффициентов . При оценке погрешности будем предполагать f(x) достаточно гладкой функцией.