19. Сравнительная характеристика методов Адамса.
Достоинства и недостатки метода Адамса.
Внешняя экономичность метода Адамса состоит в том, что функция правой части
за один шаг вычисляется один раз. В
методе Рунге-Кутта того же порядка нам
придется эту функцию вычислить 4 раза,
и если
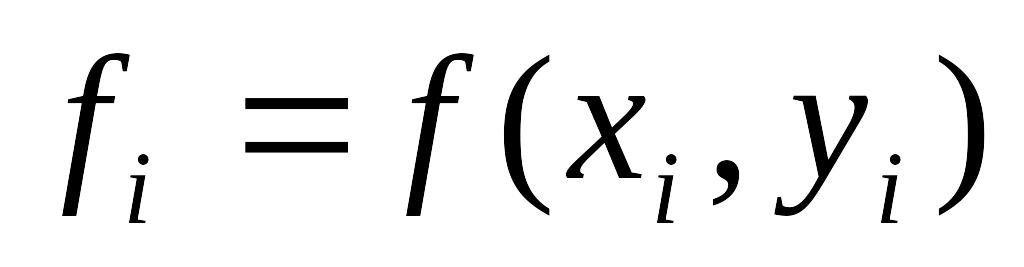выражается сложной формулой, то объем
вычислений многократно увеличивается.
Однако коэффициент остаточного члена
схемы Рунге-Кутта меньше (960 ), чем в
схеме Адамса. Значит, при одинаковой
точности решения схема Рунге-Кутта
позволяет брать шаг в
раз крупнее. Фактически функцию
вычислять нужно будет меньшее количество
раз, чем в методе Адамса.для начала счета нам необходимо знать значения функции в четырех предыдущих точках, т.е.
.,
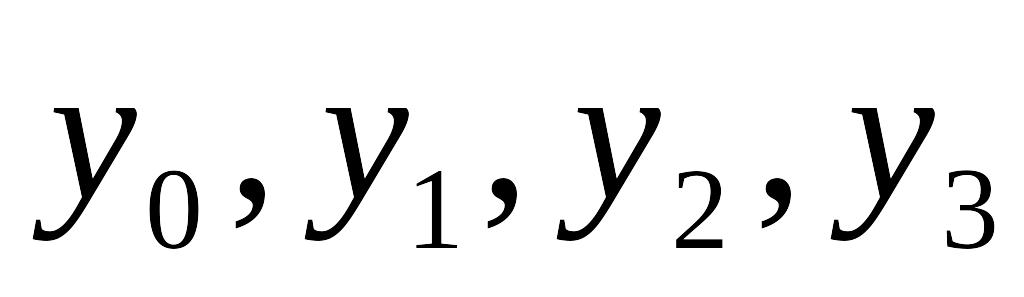что влечет увеличение объема вычислений..Формулы Адамса рассчитаны на постоянный шаг. При смене шага нужны нестандартные действия, т.е. усложнение формул.
Неявные схемы с заданным числом итераций удобны лишь для некоторых нестандартных задач. Причем для схем р-го порядка максимальное число итераций = р. Дальнейшее увеличение числа итераций не увеличивает порядок точности.
20. Повышение точности результатов при решении задачи Коши. Правило Рунге.
Точность численного решения можно повысить различными путями. В частности этого можно достичь применением разностных схем повышенного порядка точности. Однако
а) такие схемы целесообразно строить лишь для уравнений с постоянными коэффициентами, иначе алгоритмы будут слишком трудоемкими.
б) cхемы повышенного порядка аппроксимации, как правило, неустойчивы.
Если повышать точность путем уменьшения значения шага, то этот путь также ограничен, т.к.
а) должно выполняться требование экономичности, т.к. получение решения с необходимой точностью может потребовать огромного объема вычислений;
б) возможен рост вычислительной погрешности.
Поэтому на практике часто для повышения точности численного решения без существенного увеличения машинного времени используется метод Рунге. Он состоит в том, что проводятся повторные расчеты по одной разностной схеме с различными шагами. Уточненное решение в совпадающих при разных расчетах узлах строится с помощью проведенной серии расчетов.
Предположим,
проведены две серии расчетов по схеме
порядка k
соответственно с шагами h
и h/2.
В результате расчетов получены таблицы
значений сеточной функции
.
Тогда уточненное решение сеточной
функции в узлах сетки с шагом h вычисляется
по формуле
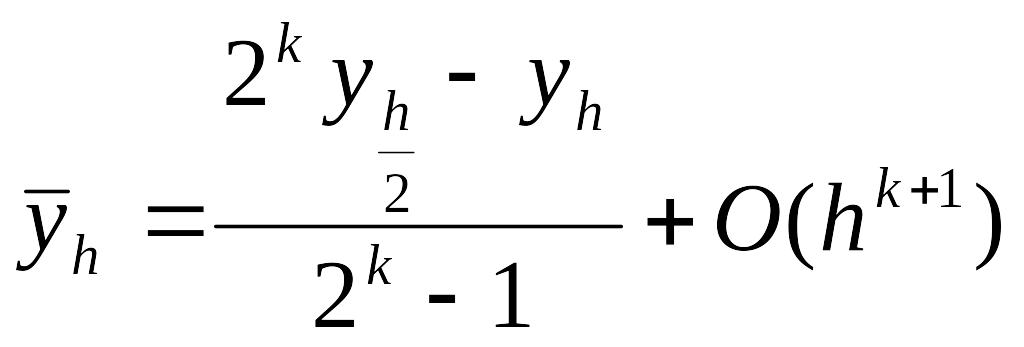(1)
Порядок точности этого решения равен k+1, хотя использовалась схема порядка k. Т.о. решение задачи на двух сетках позволяет повысить точность решения на порядок.
Для схемы Эйлера первого порядка точности формула Рунге имеет вид
(2)
Аналогично можно записать формулу для уточнения решения, полученного по методу Р-К.
21. Численные метод решения систем оду. Схема Эйлера.
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений
(1)
(2)
Здесь
- искомый вектор решения задачи (1)-(2),
заданный вектор правой части.U0
–вектор начальных условий. Запишем
задачу Коши покомпонентно
………………………………………… (3)
(4)
…………………………………………………
Задача Коши для одного обыкновенного дифференциального уравнения является частным случаем задачи Коши для системы обыкновенных дифференциальных уравнений (1)-(2). Поэтому многие из рассмотренных методов решения задачи Коши для обыкновенных дифференциальных уравнений практически без изменений могут быть перенесены на случай системы обыкновенных дифференциальных уравнений. Метод Эйлера легко распространить на систему дифференциальных уравнений первого порядка. Для простоты рассмотрим случай системы, состоящей из двух дифференциальных уравнений.
Пусть вектор
и система имеет вид
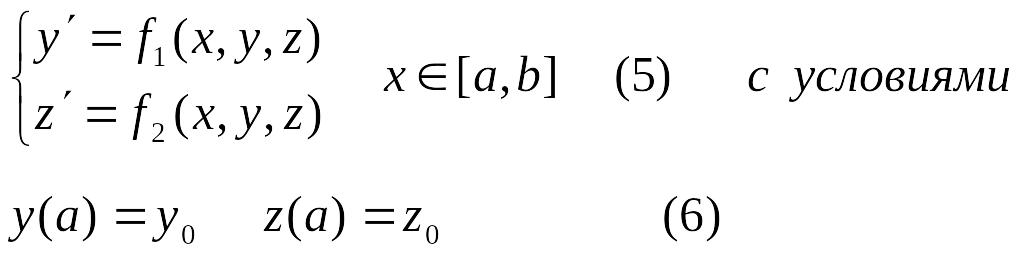
Метод Эйлера для
решения задачи (5)-(6) является
конечноразностным методом. Поэтому
введем равномерную сетку с постоянным
шагом h>0
.
Введем сеточные функции
и функции правой части
.
Приближенное решение системы (5)-(6) в
узлах
будем
вычислять последовательно по формулам:
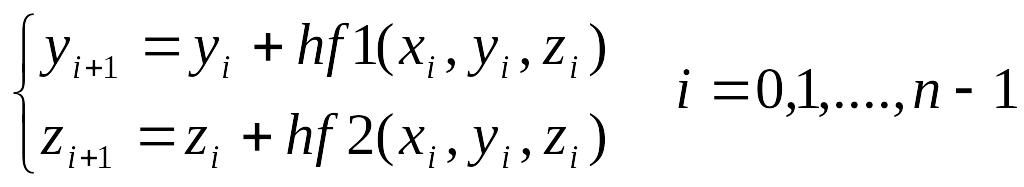(7)
Известно, что метод Эйлера обладает малой точностью. Т.е. решение получаем с большой погрешностью.