45. Интегральные уравнения. Постановка задачи. Виды линейных интегральных уравнений.

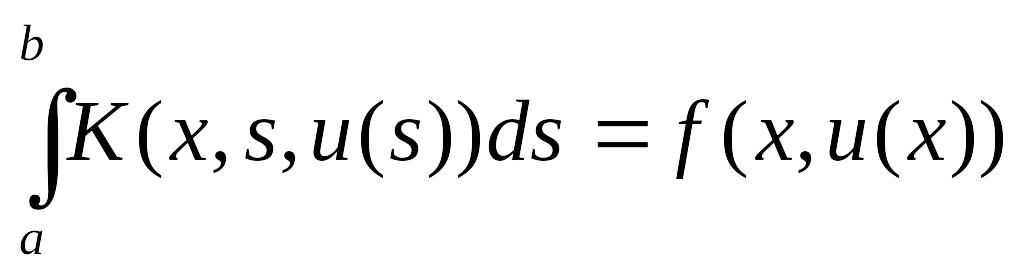
Интегральным называется уравнение, в котором неизвестная функция u(x) стоит под знаком интеграла. Одномерное (может быть нелинейное) интегральное уравнение в общем случае имеет вид (1)

где ядро K(x,s,u(s)) и правая часть f(x,u(x)) – заданные функции, s – переменная интегрирования, х - независимая переменная, u - искомая функция.

К интегральным уравнениям приводят многие инженерные или физические задачи. Например, задача восстановления переданного радиосигнала u(t) по принятому сигналу f(t) сводится к решению интегрального уравнения типа свертки

(2)

Где ядро К зависит от свойств приемной аппаратуры и среды, через которую проходит сигнал. Интегральная форма уравнений в виде законов сохранения используется также при построении консервативных разностных схем для различных типов задач (например, в механике сплошной среды). Интегральные уравнения в некоторых отношениях оказываются удобнее дифференциальных.

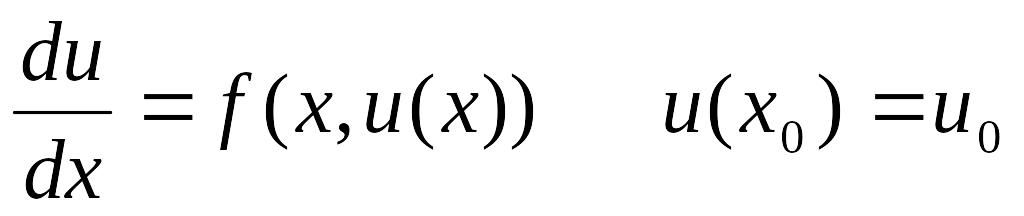
1. Интегральное уравнение содержит в себе полную постановку задачи. Например, постановку задачи Коши для дифференциального уравнения 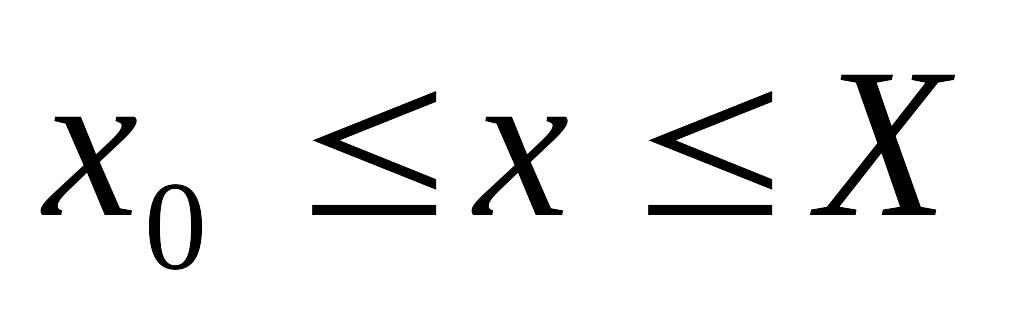(3)

можно представить в виде интегрального уравнения

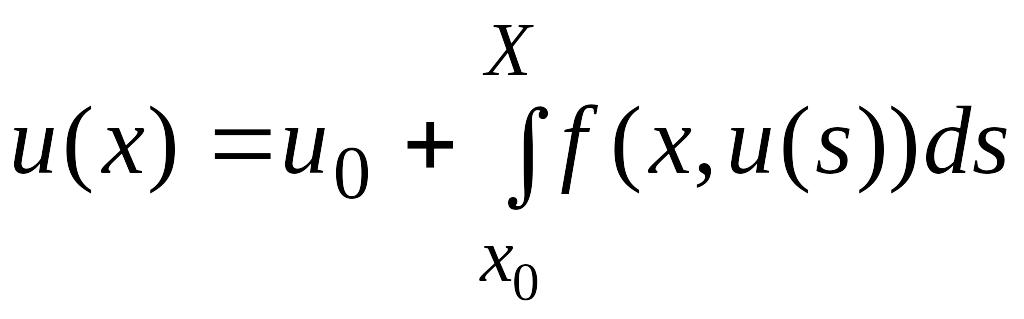(4) При этом не требуется задавать никаких дополнительных условий (начальных или граничных).

2. В интегральных уравнениях переход от одной переменной ко многим происходит очень легко. Уравнение (1) записано для случая одной независимой переменной. Многомерный аналог при наличии независимых переменных 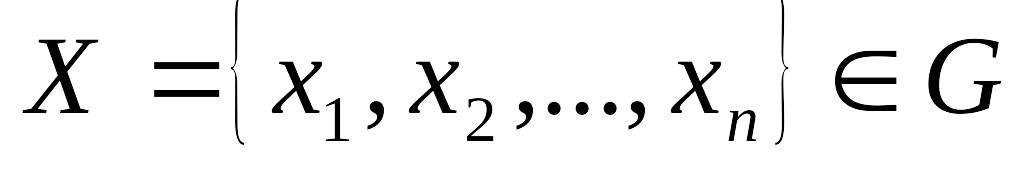запишется

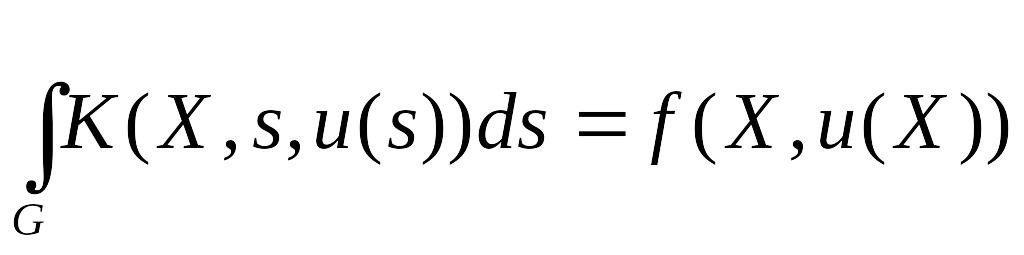(5)

Уравнение (5) отличается от (1) только тем, что интегрирование проводится по многомерной области G в рассматриваемом n-мерном пространстве. Уравнение (5) в развернутом виде может быть записано следующим образом

(6)

Поскольку оба (1) и (5) уравнения не требуют дополнительных условий и полностью определяют задачу, то теоретическое обоснование постановок и методов решения одномерных задач непосредственно обобщается на случай многих измерений.

В дифференциальных уравнениях переход от одной переменной к нескольким, т.е. от обыкновенного дифференциального уравнения к уравнению в частных производных, является принципиальным усложнением, приводит к новым постановкам задач и требует новых методов для их обоснования.

Мы будем рассматривать только одномерные уравнения вида (1) и его частные случаи.

Виды интегральных уравнений и соответствующие им задачи

Наиболее изученными и важными в практических приложениях являются интегральные уравнения вида (1), в которых неизвестная функция u(x) входит линейно. Они называются линейными интегральными уравнениями. К ним относятся

• уравнения Фредгольма первого рода 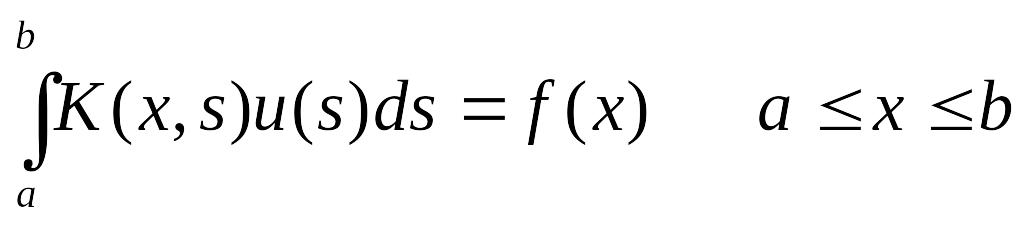(7)

• у равнения Фредгольма II рода имеют вид 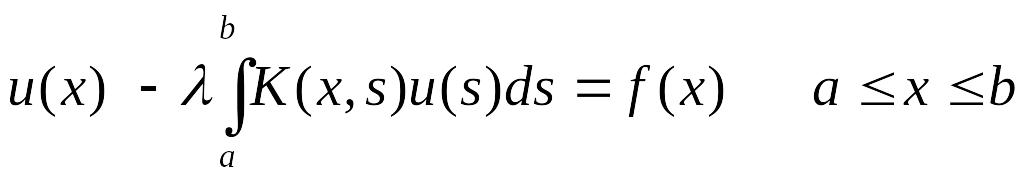(8)

В уравнениях Фредгольма ядро K(x,s) определено на квадрате axb, a sb.

Если K(x,s)=0 при x<s, т.е. ядро отлично от нуля только на треугольнике asx, axb, то уравнения (7), (8) переходят в уравнения Вольтера соответственно первого и второго рода.

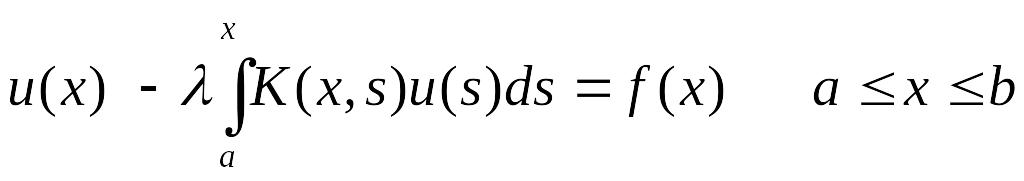(9) (10)

Ур-ия Вол теоретич иссл-ть и численно решить значит проще, чем ур-ия Фредгольма.

Задачи для уравнений I рода явл некорректно поставленными. Для их реш м.б. использованы м-ды регуляризации. Рассм-м только корректно поставленные задачи, т.е. уравнения Фредгольма и Вольтера второго рода.

Если правая часть уравнения (8) =0, то получается однородное уравнения Фредгольма II рода, которое имеет вид

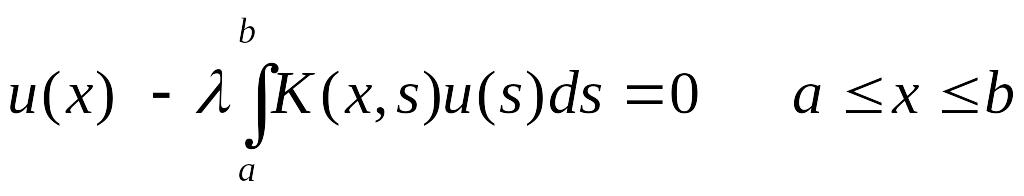(11) или 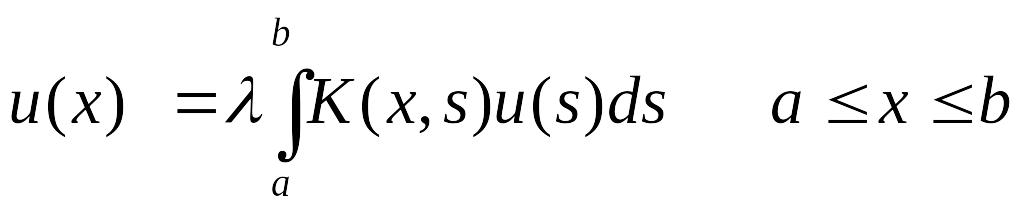(12)

Это уравнение допускает нулевое u(x)=0. Для однородного уравнения Фредгольма II рода (11) ставится задача на собст знач, т.е. требуется найти такие знач парам _, при кот-х ур-ие (12) имеет нетривиальные решения . Парам наз собст знач ядра K(x,s) или ур-ия (12), а ф-ции - собственными функциями.

На практике важным является случ, когда ур-ие Фредгольма II рода имеет вещ-ое симметрич ядро K(x,s)= K(s,x), т.к. симметрич ядро обладает следующими свойствами:

1. Симметричное ядро имеет хотя бы одно собственное значение;

2. Все собственные значения симметричного ядра действительны;

3. Собственные функции симметричного ядра ортогональны, т.е. i≠k

Для неоднород ур-ия Фредгольма (8) док-ся, что если  не явл собст знач ядра K(x,s), то ур-ие (8) имеет ед непрерывное реш u(x) для a≤x≤b. Иначе ур-ие (8) или не имеет реш или имеет их бесчисленное мн-во. При этом, если ядро K(x,s) и правая часть f(x) непрер со своими m-ыми производными, то реш u(x) также m раз непрер-но дифф-мо.

Уравнение Вольтера не имеет собст знач. Если в ур-ии (10) положить f(x)=0, то оно будет иметь только тривиальное реш u(x)=0. Поэтому неоднород ур-ие Вольтера (10) всегда имеет реш, притом ед.

Т.о. для рассматриваемых интегральных уравнений основными задачами являются:

1. Нахождение решения неоднородного интегрального уравнения при заданном значении параметра ;

2. Вычисление собственных значений и поиск соответствующих им собственных функций однородного интегрального уравнения.