16. Использование интерполяционных и квадратурных формул для построении многошаговых схем Адамса решения оду.

Приведем примеры конкретных схем Адамса.

Явные методы, т.е. . При k=1 получаем метод Эйлера,

При k=2 получим схему второго порядка аппроксимации

При k=3 получим схему третьего порядка аппроксимации

При k=4 получим схему четвертого порядка аппроксимации

При k=5 получим схему пятого порядка аппроксимации

Для неявных методов Адамса. При k=1 получаем схему 2-го порядка точности

При k=2 получаем схему 3-го порядка точности

При k=3 получаем схему 4-го порядка точности

При k=4 получаем схему 5-го порядка точности

17. Практическая реализация явной и неявной схем Адамса.

В практических расчетах чаще всего используется вариант явного метода Адамса, имеющий 4 порядок точности и использующий на каждом шаге значения сеточных функций в четырех предыдущих узлах.

На основе методов Адамса разработан целый ряд весьма сложных алгоритмов и программ для математ Для построения многошаговых схем можно использовать приемы, основанные на применении интерполяционных и квадратурных формул.

Имеем задачу Коши для обыкновенного дифференциального уравнения первого порядка

---- (1) ---- (2)

Преобразуем уравнение (1)

(3)

И проинтегрируем уравнение (3) на частичном отрезке

(4)

Интеграл от левой части выражения (4) можно легко вычислить

(5)

Чтобы вычислить интеграл правой части (4) можно использовать какую либо квадратурную формулу. Каждая квадратурная формула будет порождать соответствующую схему численного решения обыкновенного дифференциального уравнения (1).

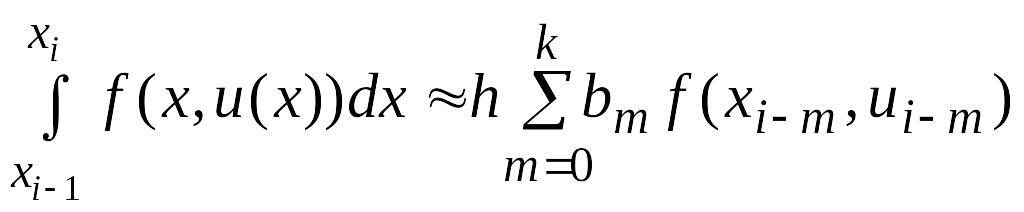(6)

На основании формул (5)-(6) можем записать разностную схему Адамса

(7)

Т.О. конкретная схема Адамса получается применением квадратурной формулы к интегралу правой части выражения (4). Можно сначала построить интерполяционный полином степени k, так чтобы на частичном отрезке аппроксимировать подынтегральную функцию , затем подставить этот полином под знак интеграла и найти интеграл в явном виде. Если для аппроксимации воспользоваться интерполяционным многочленом Ньютона, то получим явную (экстраполяционную) схему Адамса следующего вида

Алгоритм неявного (интерполяционного) метода Адамса, получаемый посредством применения интерполяционного многочлена Ньютона, имеет следующий вид

18. Многошаговые методы решения задачи Коши. Неявная схема Адамса.

В одношаговых методах поиск значения зависит только от информации в предыдущем узле . Можно добиться большей точности, если использовать информацию о значении ф-ции в нескольких предыдущих узлах, т.е . Так поступают в методах, называемых многошаговыми. Имеем задачу Коши для ОДУ первого порядка ------- (1) -------- (2)

Будем решать задачу (1)-(2) конечноразностными многошаговыми методами. Для этого введем равномерную сетку с постоянным шагом h>0. Введем сеточную функцию и функцию правой части .

Линейным k-шаговым разностным методом называется система разностных уравнений

(3)

числовые коэффициенты, не зависящие от номера узла i, параметр m=0,1,2,…,k, причем .

Из этого уравнения (3) мы можем выразить значение сеточной функции решения через ранее найденные значения. Расчет начинается с узла с номером k (i=k), т.е. c уравнения

(4)

Следовательно, для начала расчетов необходимо знать k значений сеточной функции в узлах . Значение определяется исходной задачей Коши – условием (2), т.е . Значения можно вычислить любым одношаговым методом, например методом Рунге-Кутта нужного порядка точности. Поэтому в дальнейшем можно полагать, что все необходимые значения известны.

Из уравнения (3) видно, что в отличие от методов Рунге-Кутта многошаговые разностные методы допускают вычисления правых частей только в узлах основной сетки .

Алгоритм неявного (интерполяционного) метода Адамса, получаемый посредством применения интерполяционного многочлена Ньютона, имеет следующий вид

(10)

Здесь , h- шаг сетки , - конечные разности k-го порядка, т.е.

. Коэффициент , а для остаточного члена имеет место оценка

.

Схема (10) является неявной и требует итерационного метода решения, что значительно усложняет ее применение. На практике обычно используют совместно явную и неявную формулы, получая, таким образом, метод прогноза и коррекции (предиктор-корректор). Как правило, объединяют явный и неявный методы Адамса четвертого порядка точности. Сначала используют формулу (9), чтобы получить предсказанное решение

(11)

Затем находят (12)

И далее, применяя формулу неявного метода Адамса

(13)

Метод прогноза и коррекции может быть реализован и на основе следующих формул Адамса: явной

(14)

Находим «предсказанное» значение функции, затем вычисляем и окончательно, применяя неявную формулу Адамса, получим

(15).

В целом метод (14)-(15) будет явным.