48. Метод последовательных приближений для решения интегрального уравнения Вольтера II рода.

Решение интегрального уравнения Вольтерра второго рода

(1)

будем искать в виде ряда (2)

где - система функций, подлежащая определению. Для их опреде­ления подставим (2) в (1). Будем иметь

В этом соотношении приравниваем коэффициенты при одинаковых степенях . Получим

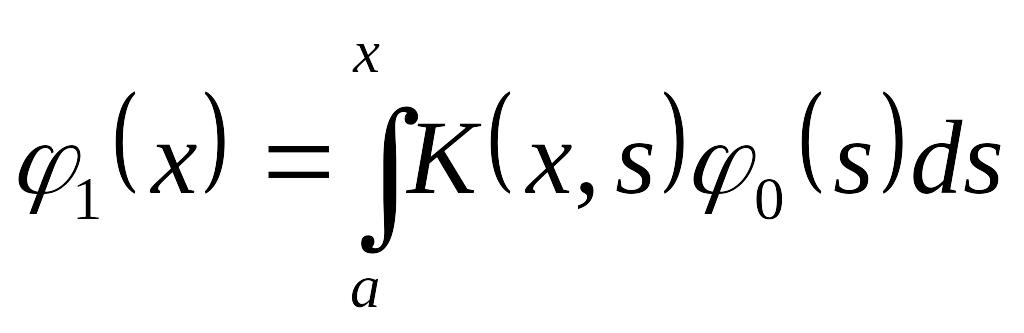=> => =>…=> (3)

Система соотношений (3) является системой рекуррентного оп­ределения . Приближенное значение решения ищется в виде (4)

Рассмотрим вопрос о сходимости этого процесса: будет ли при , или, что то же самое, будет ли при . Введем функцию . Тогда

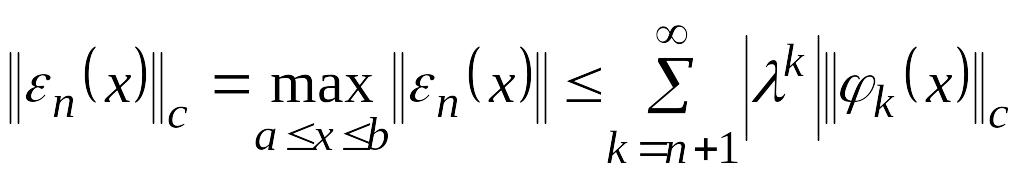
Рассмотрим вопрос о поведении при условии, что , . Из (3) будем иметь

……………………………………………………………………………………..

…………………………………………………………………………………......

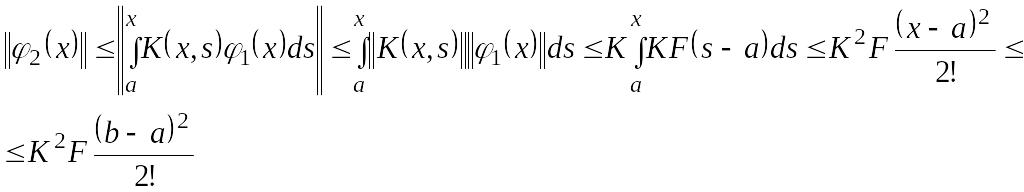
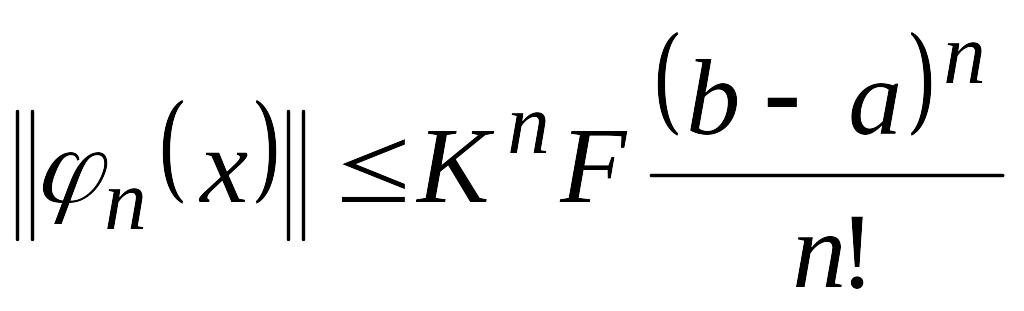
Тогда

если

49. Метод механических квадратур для решения интегрального уравнения Вольтера II рода.

Будем рассматривать интегральное уравнение Вольтерра второго рода в виде

(1)

Пусть и на взята сетка равноотстоящих точек , i= 0,1,..., N. Положим в (1) х = х_i и рассмотрим систему равенств:

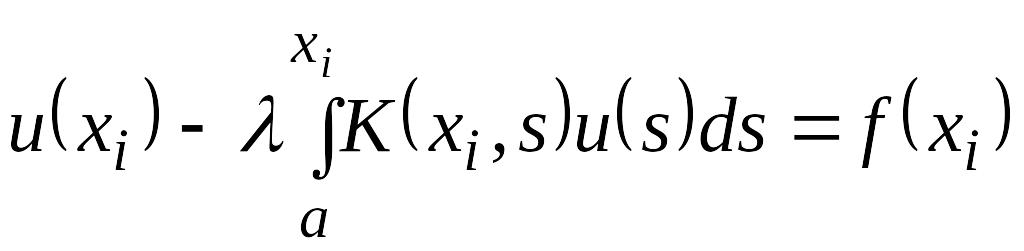i=1,2,…,N (2)

Пусть для вычисления интегрального слагаемого в (2) возьмем квадратурную формулу с узлами в точках , т.е

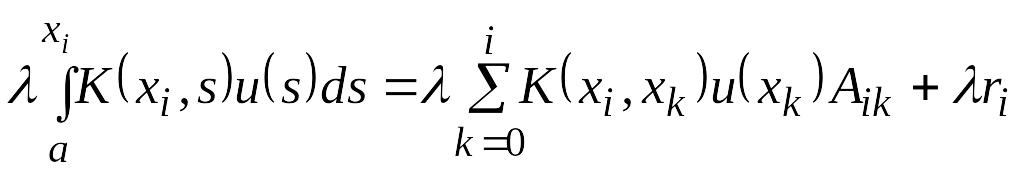
здесь - остаток квадратурной формулы. Подставим вместо интегралов в (2) их вид через эту формулу. Получим

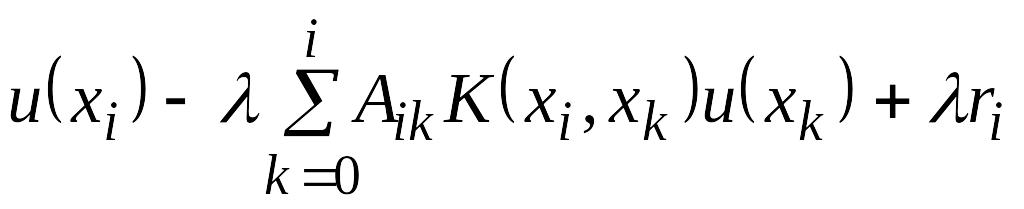i=1,2,…,N (3)

Отбрасывая остатки , получаем уравнения для приближенных значений , которые мы обозначим через y_i, следующего вида:

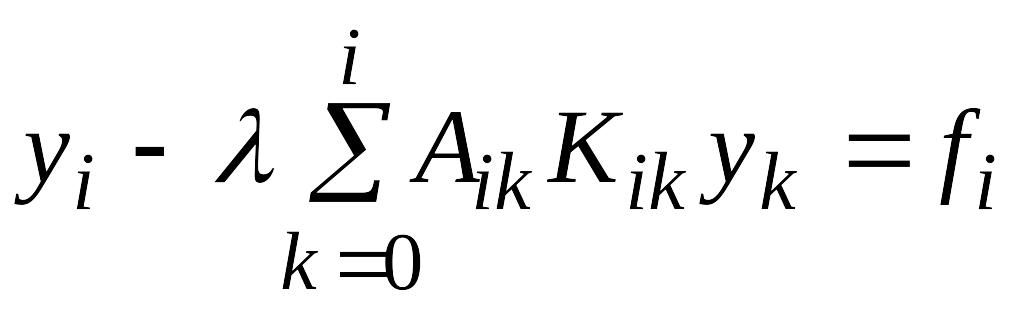
i=1,2,…,N (4)

Из последних соотношений при ограничениях на A_ik таких, что , будем иметь

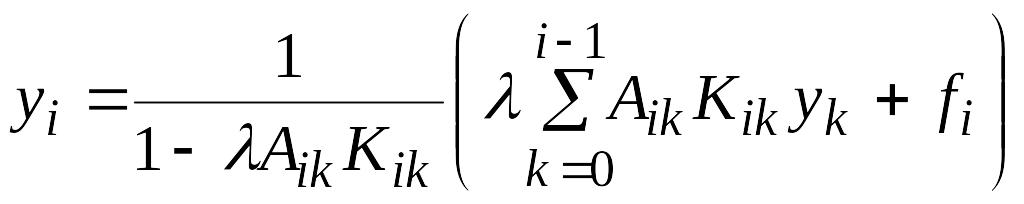i=1,2,…,N (5)

Из этих соотношений рекуррентно получим приближенные значе­ния решения уравнения (1) в узлах сетки. Более того, если для всех i выполняется неравенство | , то этот квадратурный процесс сходится.

Следует обратить внимание на необходимость составления начала расчетной таблицы при применении правила (5). Коэффициенты A_ik обычно выбираются так, чтобы локальная переменная r_i правила имела во всех узлах один и тот же порядок малости относительно h, т. е. чтобы погрешность r_i при всех i имела представление вида r_i =hⁿc_i. Предпо­ложим теперь, что нам необходимо вычислить у₁. Для этого рассмотрим квадратурную формулу при i= 1:

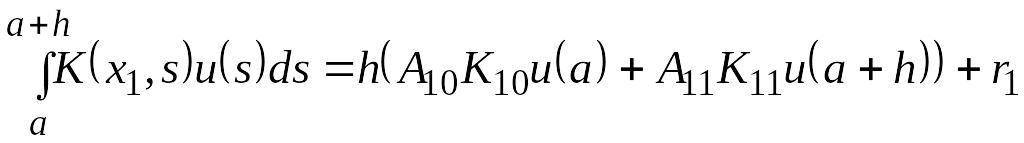
. Она содержит два числовых параметра А₁₀ и A₁₁, ко­торые мы можем выбрать так, чтобы формула имела более высокую сте­пень точности. Так как свободных параметров только два, то мы можем сделать формулу точной для многочленов первой степени. Тогда форму­ла станет известным правилом трапеций, для которого А₁₀ = А₁₁ =0.5:

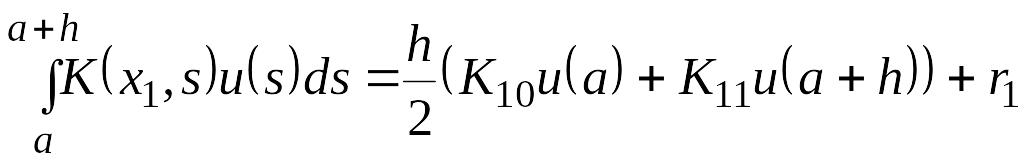
Отсюда видно, что r_i имеет относительно h третий порядок мало­сти. Если окажется, что принятый в вычислениях порядок п малости больше трех, то эту формулу нельзя применить к нахождению у₁. Тогда у₁ должно быть найдено с необходимой точностью предварительно до применения вычислительного правила (8). Аналогично, чтобы вос­пользоваться формулой (8) для нахождения у₂, будем иметь

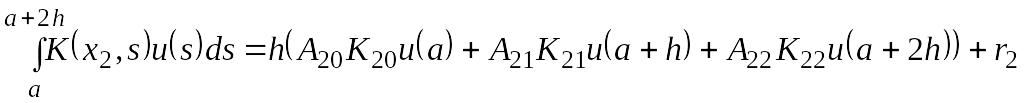
Наивысшая алгебраическая степень точности, которую можно дос­тичь при помощи выбора коэффициентов А₂₀, А₂₁, А₂₂, равна 3, и достигается она в правиле Симпсона, для которого А₂₀ = А₂₂ = 1/3, А₂₁ = 4/3:

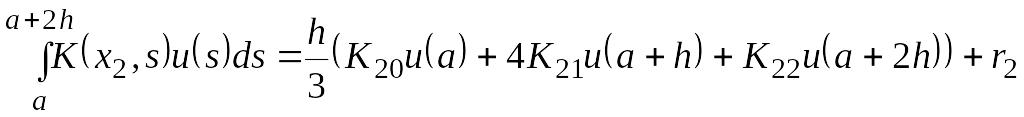
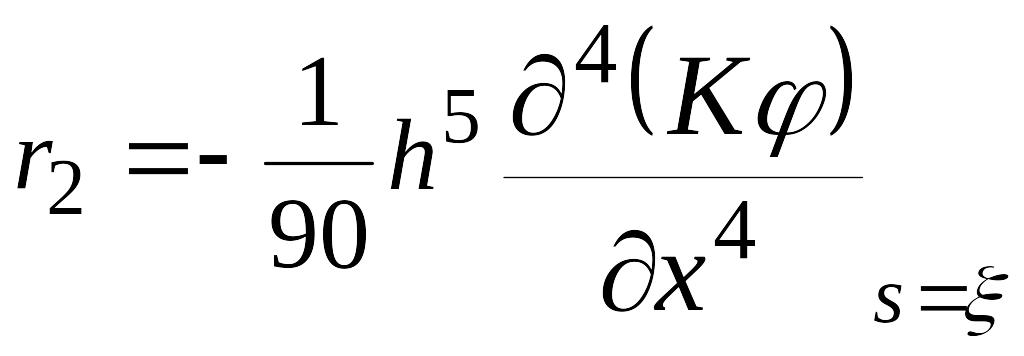
Где . Остаток r₂ имеет пятый порядок малости относительно h, и если окажется, что п > 5, то правило (5) нецелесообразно применять для вычисления у₂, а это значение, так же как и у₁, необходимо найти заранее по более точным правилам и т. д. Значение у₁ входящее в начало таблицы, можно находить, на­пример, решая интегральное уравнение в окрестности точки а при по­мощи степенного ряда, если функции К(х,s) и f(x) являются аналити­ческими функциями, или применить для вычисления этих значений фор­мулу трапеций с измененным шагом.