43. Формула трапеций
Пусть нужно найти значение определенного интеграла для непрерывной на отрезке интегрирования достаточно гладкой функции f(x) (1)
Введём на отрезке
[a,b] равномерную сетку с шагом h
,
представим интеграл (1) в виде суммы
интегралов по частичным отрезкам
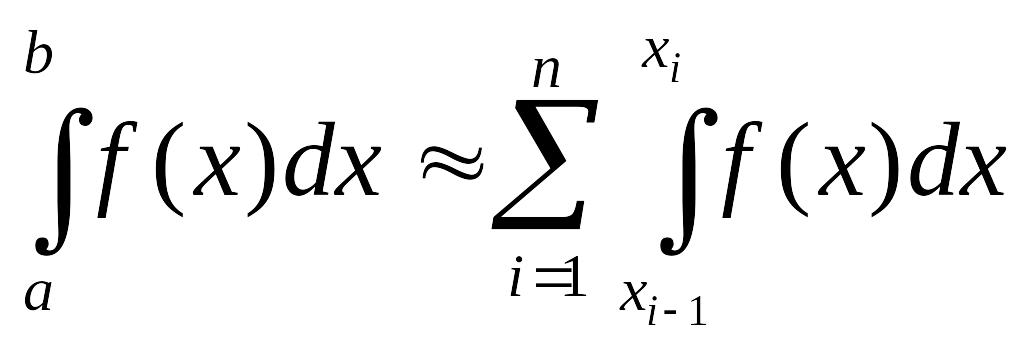(2)
Построим квадратурную
формулу трапеций для интеграла на
частичном отрезке
из геометрических соображений, т.е. этот
интеграл заменяем площадью трапеции
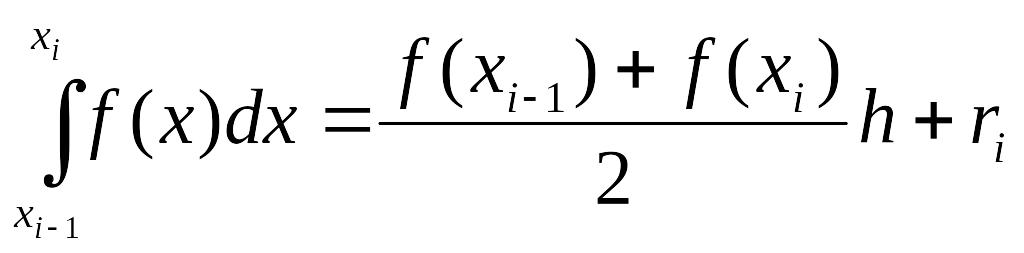(3) 
Эту
же формулу мы можем получить путем
замены подынтегральной функции
интерполяционным многочленом первой
степени, который строится по узлам
.
Запишем полином Лагранжа первой степени
на частичном отрезке
--(4)
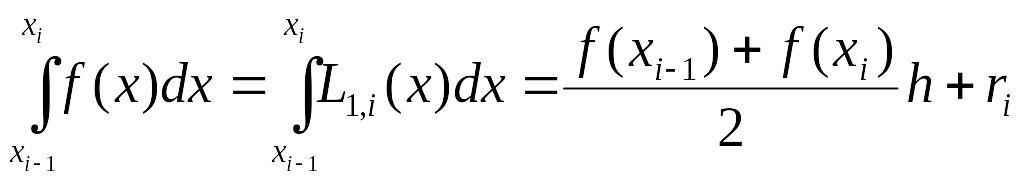--(5)
Погрешность такой
аппроксимации
(6)
Найдем погрешность квадратурной формулы трапеций для частичного отрезка
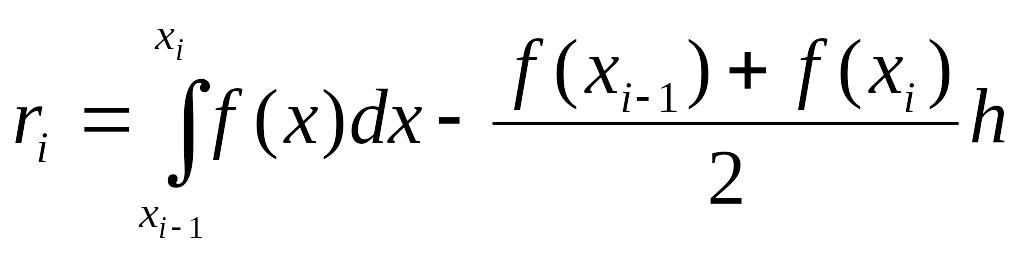Внесем полином
Лагранжа первой степени под знак
интеграла
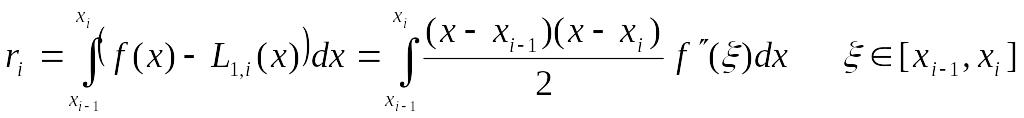(7)
Интегрируем (7) и
получаем с учетом
=>
(8)
Составную формулу трапеций получим суммированием по всем частичным отрезкам
(9)
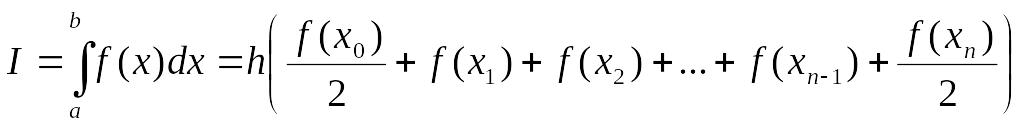(10)
Иначе
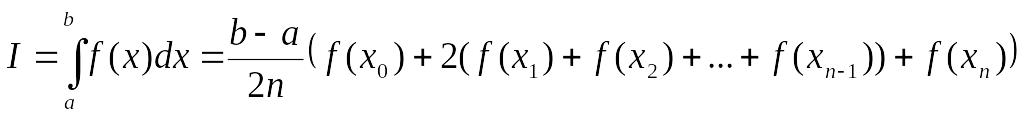(11)
Погрешность составной формулы трапеций (11) имеет следующую оценку
(12) Или
(13)
Т.о формула трапеций на всем отрезке интегрирования имеет второй порядок точности, т.е. как и формула прямоугольников.
44. Формулы Симпсона. Оценка погрешности.
Квадратурная
формула метода парабол получается, если
подынтегральную
функцию f(x)
заменяют параболой, проходящей на каждом
частичном отрезке через точки
,
т.е. интерполяционным многочленом второй
степени.
(1)
(2)
П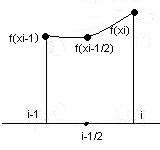
роведем
интегрирование
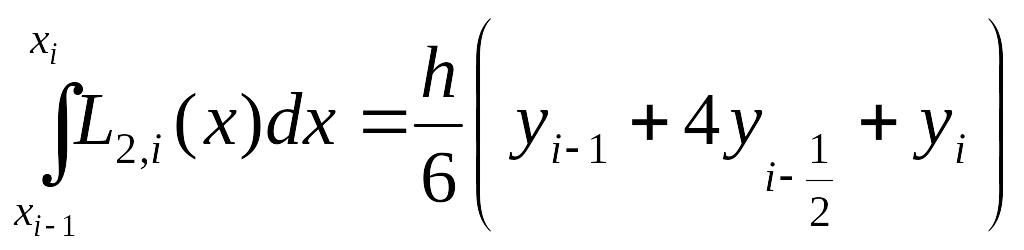(3)
Т.О. квадратурная ф-ла парабол на частичном отр-ке имеет вид
(4)
Составная формула Симпсона получается суммированием по всем частичным отрезкам
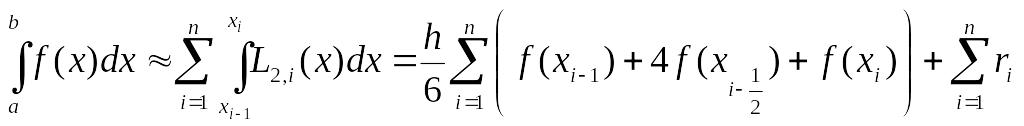(5)
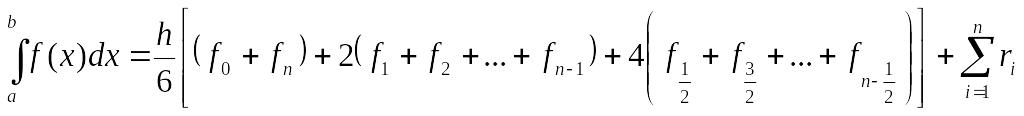(6)
Чтобы не использовать дробные индексы, можно ввести обозначения
и записать формулу
Симпсона в виде
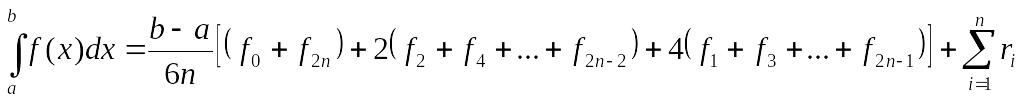(7)
Формулу Симпсона можно получить другими способами:
комбинированием формул прямоугольников и трапеций.
двукратным применением метода трапеций при разбиениях отрезка [a,b] на части с шагами h и 2h. При этом сложение проводят таким образом, чтобы главные части погрешностей этих методов уничтожились.
Из формулы кубического сплайна, построенного на отрезках
Можно показать, что погрешность формулы Симпсона на элементарном отрезке оценивается следующим неравенством
(8)
И для составной формулы парабол справедливо неравенство
(9)
Или
(10)
Таким образом, из оценок (8)-(10) видно, что формула Симпсона значительно точнее, чем формулы прямоугольников и трапеций. На частичном отрезке формула парабол имеет пятый порядок точности, а на всем отрезке интегрирования порядок точности формулы Симпсона равен 4.
Следует подчеркнуть,
что составная квадратурная формула
парабол требует четного числа разбиений
отрезка [a,b].
Если это условие не выполняется, то
интеграл вычисляют для четного количества
отрезков и к полученному значению
добавляют величину интеграла для
последнего частичного отрезка,
рассчитанную с порядком точности не
менее
.
Квадратурная формула называется точной для многочлена степени m, если при замене подынтегральной функции f(x) на произвольный алгебраический многочлен степени не выше m, приближенное равенство становится точным. В этом случае говорят, что квадратурная формула обладает m-свойством. Между максимальной степенью многочлена, для которого квадратурная формула является точной, и порядком аппроксимации по отношению к шагу h имеется связь. Формулы прямоугольников и трапеций точны для многочленов первой степени и обладают вторым порядком аппроксимации. Формула Симпсона является точной для многочленов третьей степени и имеет четвертый порядок аппроксимации.
Вышеприведенные
оценки погрешностей аппроксимационных
квадратурных формул показывают
зависимость величины остаточного
слагаемого от длины отрезка интегрирования
[a,b]
и позволяют для непрерывных функций
априорным путем вычислять шаг
интегрирования, который обеспечивает
заданную точность. Для сеточных функций
априорные оценки погрешностей выполняются
путем предварительной аппроксимации
функции
и определения соответствующей величины
максимального значения производной М
по формулам численного дифференцирования.
Далее опишем методику вычисления
интеграла в том числе и с априорным
нахождением шага h.