13. Методы Рунге-Кутта. Примеры схем различного порядка точности. Достоинства и недостатки этих методов.

Среди других явных одношаговых методов наибольшее распространение получил метод Рунге-Кутта. На его основе можно построить множество схем различного порядка точности.

Имеем задачу Коши для обыкновенного дифференциального уравнения первого порядка

(1)

(2)

Семейство явных одношаговых методов Рунге-Кутта для вычисления сеточного решения по уже известному значению этой функции в i-том узле, т.е. может быть выражено следующим образом.

(3).

Или

(4),

где

(5)

………………………………………………………….

Коэффициенты

представляют собой константы, значение которых выбирается из соображений точности, устойчивости и экономичности алгоритма. Как правило, методы Рунге-Кутта при m5 не используются. Выражения (4)-(5) описывают явный m-этапный одношаговый метод Рунге-Кутта. Используя одну из схем этого метода можно последовательно найти численное значение сеточной функции во всех узлах сетки от i=0 до n.

Схемы Рунге-Кутта имеют ряд важных достоинств.

1. все схемы, кроме схемы ломаных, имеют хорошую точность.

2. все схемы являются явными, т.е. каждое последующее значение сеточной функции 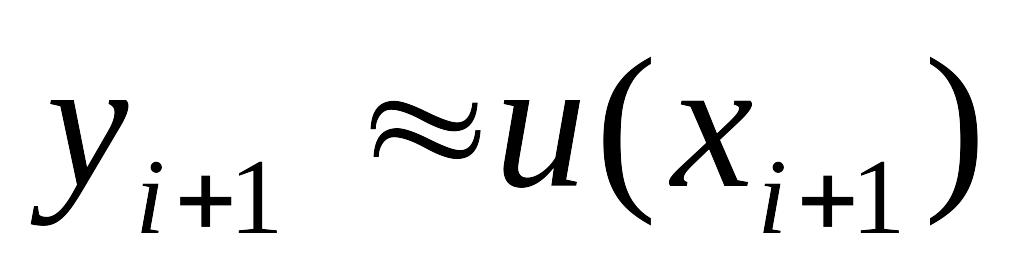вычисляется по ранее найденным значениям этой функции за определенное количество действий по аналитическим формулам.

3. все схемы допускают расчеты с переменным шагом, шаг уменьшают там, где функция быстро меняет свое значение, и увеличивают шаг в обратном случае.

4. для начала расчетов достаточно выбрать равномерную сетку, определить значение сеточной функции в начальной точке и продолжить вычисления по явным формулам конкретной схемы.

14. Многошаговые методов решения задачи Коши. Интерполяционная и экстраполяционная схемы.

В одношаговых методах поиск значения зависит только от информации в предыдущем узле . Можно добиться большей точности, если использовать информацию о значении ф-ции в нескольких предыдущих узлах, т.е . Так поступают в методах, называемых многошаговыми. Имеем задачу Коши для ОДУ первого порядка ------- (1) -------- (2)

Будем решать задачу (1)-(2) конечноразностными многошаговыми методами. Для этого введем равномерную сетку с постоянным шагом h>0. Введем сеточную функцию и функцию правой части .

Линейным k-шаговым разностным методом называется система разностных уравнений

(3)

числовые коэффициенты, не зависящие от номера узла i, параметр m=0,1,2,…,k, причем .

Из этого уравнения (3) мы можем выразить значение сеточной функции решения через ранее найденные значения. Расчет начинается с узла с номером k (i=k), т.е. c уравнения

(4)

Следовательно, для начала расчетов необходимо знать k значений сеточной функции в узлах . Значение определяется исходной задачей Коши – условием (2), т.е . Значения можно вычислить любым одношаговым методом, например методом Рунге-Кутта нужного порядка точности. Поэтому в дальнейшем можно полагать, что все необходимые значения известны.

Из уравнения (3) видно, что в отличие от методов Рунге-Кутта многошаговые разностные методы допускают вычисления правых частей только в узлах основной сетки . Многошаговые методы можно разделить на явные и неявные.

Метод (3) называется явным, если коэффициент в правой части .

(5)

Схема (5) иначе называется экстраполяционной. Искомое значение сеточной функции в этом случае выражается явным образом через k предыдущих значений.

(6)

Если коэффициент , то метод называется неявным или интерполяционным. Тогда для нахождения значения сеточной функции необходимо решить нелинейное уравнение вида

Где (7)

Обычно это уравнение (7) решают методом Ньютона, выбирая начальное приближение .