50. Решение интегральных уравнений. Метод замены ядра на вырожденное.

Ядро уравнения Фредгольма второго рода

(1)

называется вырожденным, если оно может быть представлено в виде суммы конечного числа членов вида

(2)

т.е. каждый член разложения можно представить в виде произведения известных функций одной переменной , . Функции А(х) и В(s) известны и являются линейно независимыми. (для уравнения Вольтера ядро не может быть вырожденным, т.к. иначе оно тождественно равнялось бы нулю). Предполагая, что решение интегрального уравнения (1) с вырожденным ядром (2) существует, и будем искать его в виде суммы конечного числа некоторых элементов следующего вида

(3)

где - некоторые числовые коэффициенты, которые достаточно просто можно определить через и . В самом деле, подставив (3) в (1) и учитывая (2), получим

(4)

Чтобы найти численное значение коэффициентов (4), построим линейную систему уравнений следующим образом. Подставим соотношение (3) в (4)

(5)

Введем следующие обозначения:

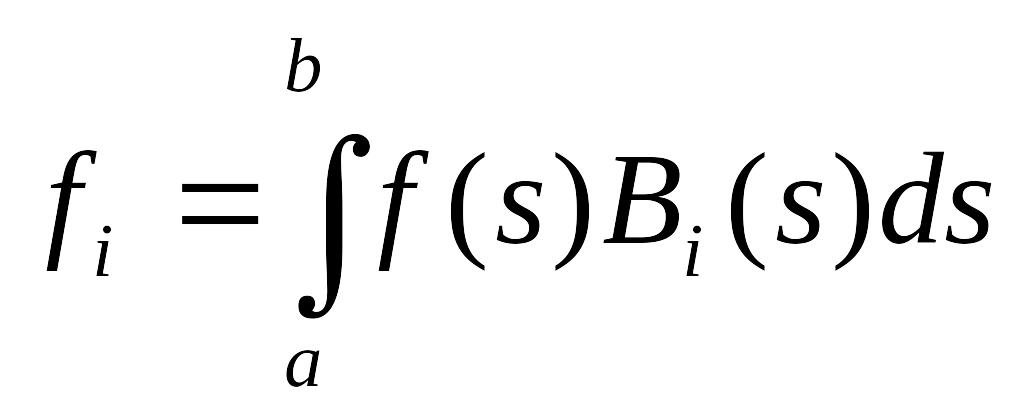i,j=1,2,…,n (6)

Получили линейную систему уравнений относительно неизвестных

(7)

Решая эту систему и подставляя найденные значения в (3), найдем искомое значение функции u(x).

Построе­ние решения u(х) сводится в случае вырожденного ядра К(х, s) к вы­числению величин и решению системы линейных алгебраических уравнений (7). Если эти величины будут определены точно, то полу­чим точное решение исходного интегрального уравнения.

В ряде случаев произвольное ядро удается хорошо аппроксимировать вырожденным ядром. Тогда решение полученного аппроксимирующего уравнения принимается в качестве приближенного решения исходного уравнения. Способов построения для заданного ядра вырожденного и близкого ядра существует несколько. В качестве ядра можно взять отрезок ряда Тейлора, ряда Фурье или воспользоваться каким-либо правилом интерполирования.

Применение степенного ряда эффективно в случае, когда ядро является аналитической функцией от s в области , где с есть середина отрезка [a,b] и . В этом случае ядро можно разложить в степенной ряд по степеням (s-c), сходящийся в круге . Коэффициенты этого ряда будут зависеть от х:

где . В качестве вырожденного ядра К(х, s) может быть взят конечный отрезок степенного ряда

Аналогично можно поступать и в тех случаях, когда ядро есть аналитическая функция от х или от обоих аргументов.

При использовании интерполяционных методов поступают следующим образом. Выбирают на отрезке [a,b] n узлов s₁,s₂,...,s_n и интерполируют по аргументу s функцию по ее значениям в выбранных точках s₁,s₂,...,s_n. При этом будет получено приближенное представление ядра исходного уравнения :

и может быть принято за вырожденное ядро.

Оценки точности таких приближений очень громоздки и в практике неудобны. Из-за сложности вычисления интегралов в аппроксимирующих выражениях методы последовательных приближений и замены ядра на вырожденное используются редко, но эти методы полезны для нахождения первых приближений к решению интегрального уравнения.

При решении уравнения Вольтера СЛАУ (5) имеет треугольный вид и легко решается методом последовательного исключения неизвестных ( по аналогии с обратным ходом Гаусса).