46. Метод последовательных приближений для решения интегрального уравнения Фредгольма II рода.

Простейшим методом решения интегральных уравнений является метод последовательных приближений. Рассмотрим неоднородное уравнение Фредгольма второго рода, записав его следующим образом

(1)

Для решения (1) построим итерационный процесс, аналогичный методу простой итерации для решения нелинейного уравнения. Пусть – начальное приближение искомой функции u(x). Обычно полагают . Подставим в правую часть уравнения (1), получим выражение для первого приближения:

(2)

Подставляя найденное приближение в подынтегральное выражение в (1) , найдем следующее приближение

и т.д.

Аналогично, подставляя найденное на k-ой итерации приближение в подынтегральное выражение, найдем k+1 приближение

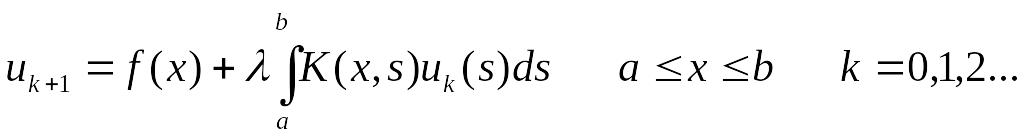(3)

При достаточно малом значении параметра  и ограниченном ядре K(x,s) этот итерационный процесс сходится равномерно по х, причем сходимость линейная. Достаточное условие сходимости имеет вид

q=M||(b-a)<1, M=max|K(x,s)| для любых x,s (4)

47. Метод механических квадратур для решения интегрального уравнения Фредгольма II рода.

Методы этого класса могут применяться для решения как линейных, так и нелинейных интегральных уравнений. В их основе лежит использование формул численного интегрирования для вычисления определенных интегралов, входящих в исходное интегральное уравнение.

Рассмотрим нелинейное в общем случае интегральное уравнение

(1)

Введем в квадрате [a≤x≤b, a≤s≤b] по каждой стороне сетку , где – узлы сетки, i=0,1,…,n; - шаг сетки, i=0,1,…,n-1. В частном случае сетка выбирается равномерной, т.е. и h=(b-a)/n - шаг сетки. Заменим интеграл в уравнении (1) некоторой квадратурной формулой с помощью значений сеточной функции в узлах: (2)

где - соответственно коэффициенты и остаток квадратурной формулы численного интегрирования. Рассматривая соотношение (2) в каждой точке построенной сетки, мы построим систему (в общем случае нелинейных) алгебраических уравнений. Величина остатка квадратурной формулы может быть отброшена как достаточно малая величина. Имеем (3)

Решая систему (3) любым известным методом (например, методом Ньютона), получим значения сеточной функции в выбранных узлах сетки на отрезке [a,b]. Используя полиномы Лагранжа или Ньютона и полученные значения сеточной функции , можно построить аналитический вид приближенного решения

Вопрос сходимости сеточного решения уравнения к значению искомой функции при n может быть рассмотрен лишь для конкретного вида интегрального уравнения. В общем случае исследовать сходимость численного метода для решения интегрального уравнения очень трудно. Как правило для одномерных задач решение имеет хорошую точность, а для двумерных – удовлетворительную.

Рассмотрим линейные интегральные уравнения. Для однородного уравнения Фредгольма второго рода вида запишем, отбросив остаток квадратурной формулы, сеточное уравнение аналогичное равенству (3)

(4)

Уравнение Фредгольма линейно, поэтому полученная система (4) тоже линейная. Перепишем ее в следующем виде (5)

Система уравнений (5) представляет собой задачу на собственные значения матрицы А n-го порядка, элементами которой являются числа . Матрица А имеет n собственных значений, которые являются приближениями к собственным значениям ядра K(x,s) однородного уравнения Фредгольма. Разностное уравнение (5) решается известными методами. Матрица А этого уравнения является плотно заполненной и неэрмитовой, поэтому фактически вычислить разностное решение удается при небольших n50. Получить в этом случае хорошую точность можно лишь для нескольких первых собственных значений, причем ядро и правая часть должны быть достаточно гладкими и не быстропеременными.

В случае неоднородного уравнения Фредгольма II рода вместо однородной системы (4) получим следующую систему линейных алгебраических уравнений

(6)

Эта система уравнений легко вычисляется методом Гаусса. Система (6) имеет единственное решение, если параметр  не является собственным значением интегрального уравнения Фредгольма. Если значение этого параметра попадает в окрестность некоторого собственного значения, то система (6) становится плохо обусловленной и сеточное решение может сильно отличаться от искомых значений .

На практике обычно собственные значения интегрального уравнения неизвестны, поэтому, чтобы исключить попадание  в окрестность собственных значений, ограничиваются исследованием практической сходимости. Проводят серию расчетов со сгущающейся сеткой. Если при этом наблюдается сходимость сеточных значений, то результаты последнего расчета на густой сетке принимают в качестве искомого решения. Если расчет хотя бы на одной из сеток выпадает из общей закономерности (сходимости), то имеет место случайное попадание параметра  в окрестность собственного числа. Если сходимости нет на всех сетках, это означает совпадение параметра с собственным значением, т.е. при s<x.

Решив систему (6), определим приближенное решение исходного интегрального уравнения в узлах сетки. Для получения аналитического выражения решения подставим найденные при­ближенные значения в (6), получаем приближенное решение в виде (7)

Для сходимости сеточного решения уравнения к значению искомой функции при n важным является выбор квадратурной формулы. Т.к. большинство задач решается как правило с небольшим числом узлов, то для получения хорошей точности целесообразно выбирать квадратурные формулы высокого порядка точности. Если ядро и правая часть имеют достаточное количество производных, то целесообразно применять формулы типа Гаусса. Можно также использовать простейшую формулу трапеций, последовательно сгущая сетки вдвое и уточняя решение методом Рунге.

Если в качестве квадратурной формулы выбрана составная формула трапеций, то значения коэффициентов этой формулы будут следующими:

i=2,3,…,n-1 ; i=1,2,..,n; h=(b-a)/(n-1)

Если в качестве квадратурной формулы выбрана составная формула Симпсона, то полагаем n=2m+1 и тогда значения коэффициентов этой формулы будут следующими:

; i=1,2,..,2m+1; h=(b-a)/(2m)

В качестве квадратурной формулы можно выбрать практически любые квадратуры. Значения коэффициентов и значения узлов в этом случае записываются аналогичным образом.