26. Методы решения граничных задач для оду. Общая характеристика.

Методы решения краевых задач подразделяются на точные (аналитические), приближенные и численные.

Аналитические методы изучаются в курсе дифференциальных уравнений и применимы для достаточно узкого класса задач. В частности хорошо развиты аналитические методы для решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Приближенные методы поиска решения граничных задач разрабатывались задолго до появления вычислительных машин. Суть их состоит в том, что для отыскания решения краевой задачи выбирается некоторая линейно независимая система дифференцируемых функций . Причем, как правило, функция удовлетворяет граничным условиям. Искомое решение строят в виде линейной комбинации функций . (7)

или развернуто (8)

Подставляя решение (8) в исходное уравнение мы получим невязку, т.е. разность между левой и правой частями уравнения. Невязка является функцией переменной x и параметров и для уравнения (4) выражается следующим образом

(9)

Коэффициенты подбираются таким образом, чтобы значение невязки было минимальным. Способ вычисления этих коэффициентов и определяет тот или иной приближенный метод.

1. В методе коллокаций выбирают n точек 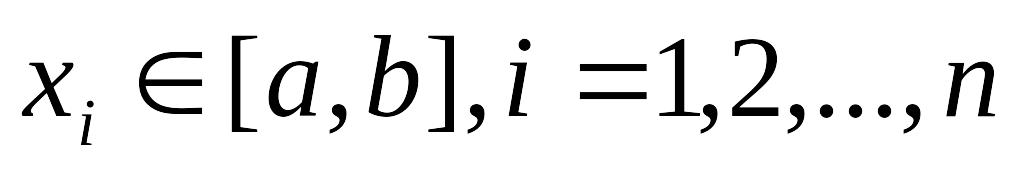, которые называют точками коллокаций. Невязка (9) в точках коллокации приравнивается к нулю.

(10)

Таким образом получаем систему n линейных алгебраических уравнений, решение которой даст конкретные значения коэффициентам .

2. Метод наименьших квадратов основан на минимизации суммы квадратов невязок в заданной системе точек 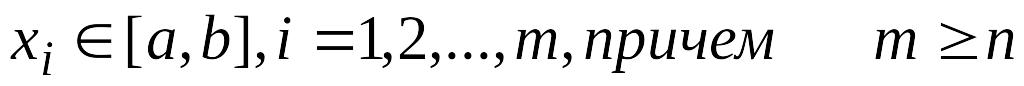. Запись этого условия также даст систему n линейных алгебраических уравнений для определения значений коэффициентов .

3. В основу метода Галеркина положено требование ортогональности системы базисных функций и невязки 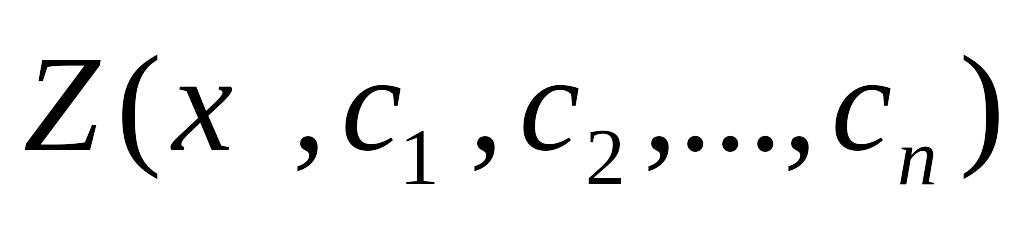. Это требование выражается в виде определенного интеграла по отрезку [a,b] и приводит в конечном итоге к построению системы из n линейных алгебраических уравнений. Решая построенную систему, определим значения параметров и затем получим конкретное выражение приближенного решения (7).

Аналогичным образом строятся другие приближенные методы. Все они сводятся к формированию системы из n линейных алгебраических уравнений.

Численные методы можно условно разделить на две группы: методы сведения решения краевой задачи к последовательности решений задач Коши и непосредственное применение разностных методов. Среди методов первой группы различают

• Метод вариации постоянных (метод редукции)

• Метод стрельбы

• Метод дифференциальной прогонки.

27. Метод редукции для решения краевых задач.

Пусть на отрезке [a,b] задано линейное обыкновенное дифференциальное уравнение n-го порядка с непрерывными коэффициентами и функцией правой части f(x) (1)

Или в развернутом виде (2)

При этом .

Кроме этого на отрезке заданы граничные условия вида

(3)

Требуется найти решение поставленной краевой задачи (2)-(3) на отрезке [a,b] методом редукции. Суть этого метода состоит в том, чтобы поиск решения свести к решению задач Коши.

Из курса дифференциальных уравнений известно, что искомое решение задачи (2)- (3) можно представить в виде линейной комбинации (4)

Где Y0 – является частным решением неоднородного дифференциального уравнения (2), а Yi ,i=1,2,…,n– линейно независимые решения однородного дифференциального уравнения

, - произвольные константы. Для определения этих констант используют краевые условия (3), в которые подставляют решение в виде (4).

Предположим, что функции Yi ,i=0,1,2,…,n уже известны, и потребуем, чтобы для решения (4) выполнялись краевые условия (3). Таким образом, имеем систему n уравнений с неизвестными . Если построенная система имеет единственное решение, то решение приближенное задачи (2)-(3) будет найдено по формуле (4) единственным образом.

Чтобы найти функции Yi ,i=0,1,2,…,n чаще всего поступают следующим образом. Функцию Y0 определяют по неоднородному уравнению (1) с нулевыми начальными условиями . (5)

Функции Yi ,i=1,2,…,n находят как решение однородного уравнения (6)

с такими начальными условиями k=0,1,…,n-1 (7)

Таким образом, метод редукции к задачам Коши состоит из следующих этапов.

1. На отрезке поиска решения [a,b] любым известным методом находим численные решения Yi ,i=0,1,2,…,n

2. Используя общий вид решения (4) и краевые условия (3), определяем коэффициенты .

3. Вычисляем по формуле (4) искомое решение задачи (2)-(3)

Необходимо отметить, что метод редукции применим только для решения граничных задач на основе линейных дифференциальных уравнений. Однако при реализации метода редукции иногда возникает потеря точности. Это происходит в тех случаях, когда функции решения однородного уравнения Yi ,i=1,2,…,n являются быстрорастущими функциями, а само решение исходной задачи y(x)u(x) таковым не является. Большие вычислительные погрешности возникают из-за линейного комбинирования быстрорастущих функций.