9.6Алгебраические критерии устойчивости

Акцентируем теперь внимание на то обстоятельство, что проверка условия устойчивости характеристического многочлена не требует вычисления всех его корней, а лишь выяснения того, расположены ли корни только в левой полуплоскости комплексной переменной P.

Нельзя ли установить этот факт, не находя корней?

Ответ на этот вопрос положительный. Алгебраическая проблема проверки устойчивости многочленов была впервые поставлена Максвеллом. Детальное и простое изложение этой проблемы содержится в книге «Устойчивые многочлены» Пестиков М.М.– М. Наука, 1981 -175 с.

Прежде всего, установим необходимое условие устойчивости.

Теорема. Если многочлен Q(P) с устойчив, то все его коэффициенты положительны a_n>0.

Доказательство теоремы

Используем разложение многочлена Q(P) на простые двучлены и трехчлены. Каждому вещественному корню соответствует двучлен , каждой паре комплексно сопряженных корней - трехчлен , если все , , то коэффициенты во всех двучленах и трехчленах положительны, следовательно, положительны и коэффициенты в многочлене Q(P), являющимся их произведением.

Пример 1 Многочлен , заведомо неустойчив, поскольку коэффициент при P₂ равен нулю.

Выполнение условия необходимости не гарантирует устойчивости многочлена при любом n, хотя оно достаточно при n=1, и n=2. При больших (n>2) приходится использовать более сложные процедуры. Кроме того, как известно из алгебры для уравнений 3 и 4 степени имеются общие формулы для нахождения корней, а для уравнений 5степени и выше, таких формул нет. Поэтому для систем выше 2 порядка особенно важны условия, которые позволяли бы судить об их устойчивости, не вычисляя корней характеристического уравнения. Такие условия называются критериями устойчивости.

9.7Критерий устойчивости Гурвица

Для формулировки критерия Гурвица составим из характеристического уравнения определитель n-го порядка.

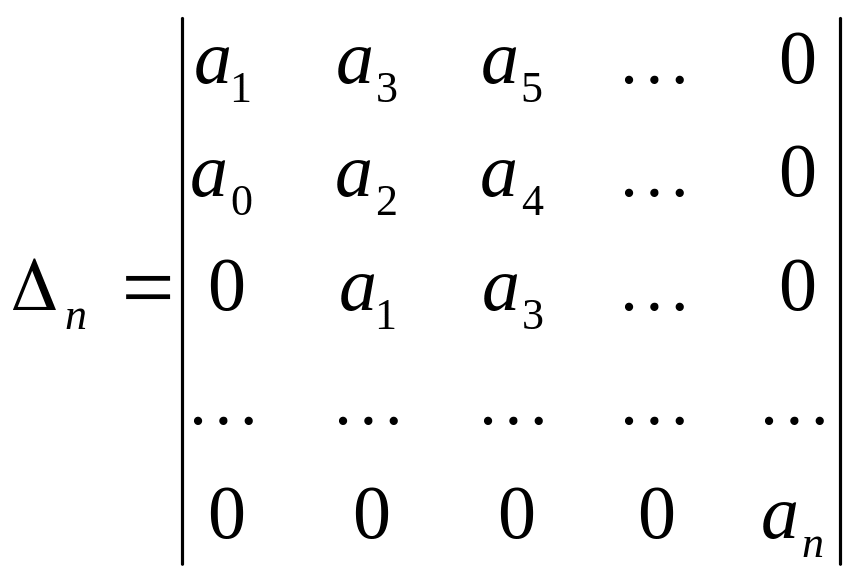
На главной диагонали, которого располагаются коэффициенты в порядке возрастания их индексов, начиная с a₁ кончая a_n. В каждом столбце при движении от элемента, находящегося на главной диагонали, вверх индексы коэффициентов возрастают, вниз убывают, при этом на месте элементов с индексами, превышающими n (при движении вверх) и отрицательными индексами (при движении вниз), проставляются нули. Запишем частные миноры определителя

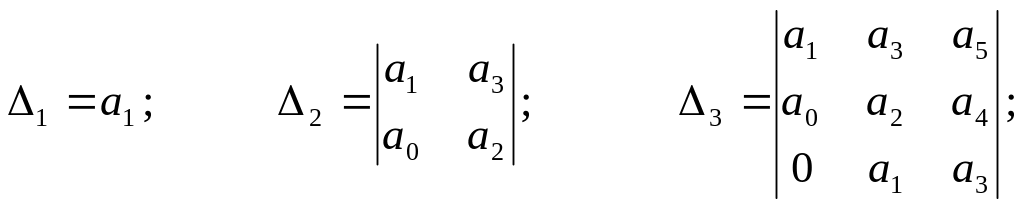и.т.д.

Назовем эти миноры, включая определитель , определителями Гурвица.

Формулировка критерия устойчивости Гурвица

Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица, составленные из коэффициентов её характеристического уравнения, были больше нуля (при a₀>0).

i=1,n при a₀>0

Из этого критерия следует, что при n=3, необходимое и достаточное условие устойчивости имеет вид.

Пример. Используем устойчивость системы в разомкнутом и замкнутом состояниях. Характеристическое уравнение разомкнутой системы . Необходимое условие не выполняется, т.к. при  коэффициент a₂=0. Поэтому разомкнутая система неустойчива.

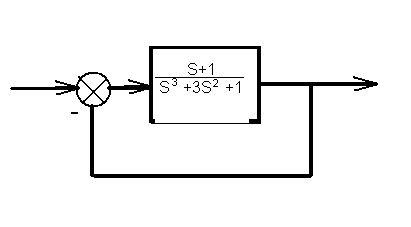
Характеристическое уравнение замкнутой системы.

Проверим

Замкнутая система устойчива.