6.5Частотные функции

Если входное возмущение представляет собой гармоническое колебание , то передаточная функция превращается в частотную функцию или в частотную характеристику линейной системы

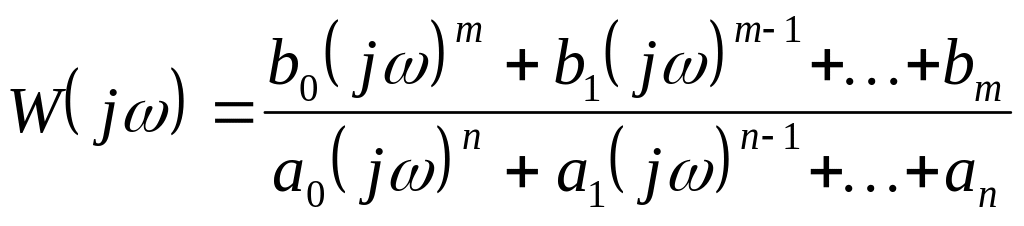- называется частотной передаточной функцией.

Ее можно представить в виде:

(6.24.)

где ; ; (6.25.)

A()- амплитудно-частотная характеристика;

()- фазочастотная характеристика.

Рисунок 6‑25 Частотная передаточная функция

На комплексной плоскости частотная передаточная функция определяет вектор 0C (длина) модуль - АЧХ, ( )- фазочастотная характеристика (рис 6-3).

Физический смысл частотной характеристики

Установим, какой же физический смысл имеют частотные характеристики. Если на вход устойчивой линейной системы (стационарной) подается гармонический сигнал , то на ее выходе после окончания переходного процесса устанавливается гармонический процесс с амплитудой в b и фазой  сдвинутой относительно фазы входного сигнала на угол (рис 6-5)

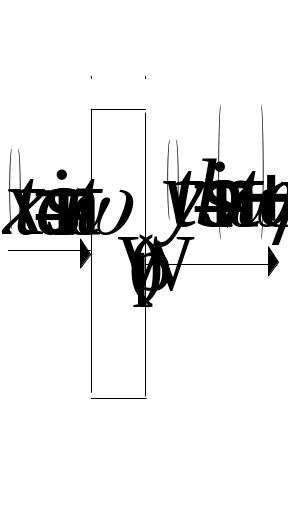
Рисунок 6‑26 Линейная система

Амплитуда b и сдвиг фазы  зависят от частоты входного сигнала и свойств системы. Кроме того, амплитуда b зависит еще от амплитуды входного сигнала а. Но отношение не зависит от амплитуды a. Оказывается, что и , то есть амплитудная частотная функция равна отношению амплитуды выходного сигнала к амплитуде входного гармонического сигнала (в установившемся режиме), а фазовая частотная функция сдвигу фазы выходного сигнала.

Логарифмические частотные характеристики (ЛЧХ)

Кроме перечисленных логарифмических частотных характеристик используются (ЛЧХ) - логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ).

ЛАЧХ - это график зависимости от логарифма частоты . При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе (на отметке, соответствующей значению , указывают значение , а по оси ординат - L()).

ЛФЧХ - это график зависимости фазовой частотной функции () от логарифма частоты .

6.6Временные характеристики сау. Понятие о функции Грина

Для описания нелинейных детерминированных систем очень полезным является понятие функция Грина.

Пусть L представляет собой операторы дифференцирования, интегрирования и умножения на константу.

Например: ;

где - выходной процесс, - входной процесс, a₀, a₁, a₂ - постоянные коэффициенты. Это линейные уравнения второго порядка. Видно, если - является решением уравнения , то - также решением. Если y и z - решения уравнения, то и , то есть

y+ z - также являются решением.

Рассмотрим x₁ решение уравнения и решение x₂ решение уравнения . Тогда . Это наш первый и очень полезный результат, из которого вытекает следующее очень важное заключение:

Любое сложное входное воздействие можно представить в виде суммы составляющих, для каждой из которых уравнение можно решить отдельно. Складывая их, можно получить решение, соответствующее полному входному воздействию .

1. то есть ;

Например - ряд Фурье.

2. можно выбрать и другой набор

Это импульсные функции единичной интенсивности. Отклик на такой импульс имеет характер затухающих колебаний.

Общее решение получается в результате интегрирования по всем откликам, соответствующим импульсам, которые образуют входное воздействие. В этом заключается идея метода функций Грина.

Понятие функции Грина

Чтобы решить уравнение , где L= p линейный дифференциальный оператор. Предположим, что мы нашли оператор, обратный к L (обозначим его через L^-1), такой что (где I - тождественный оператор). Например, если , то L^-1 является оператором интегрирования ; .

Для дифференциального оператора общего вида можно предположить, что

L^-1 представляет собой интегральный оператор с ядром , то есть

(6.26.)

Если найдено ядро G, то с помощью этого равенства можно найти решение дифференциального уравнения. Причем - это функция Грина, которая является очень полезным понятием. Это мы раскроем чуть позже.

Действуя вновь оператором по (1), получаем

(6.27.)

Поскольку оператор интегрирования и дифференцирования являются линейными, то их можно поменять местами. Тогда первая часть

(6.28.)

И поскольку слева, очевидно стоит , то получаем

(6.29.)

Известно, что должно иметь следующее соотношение

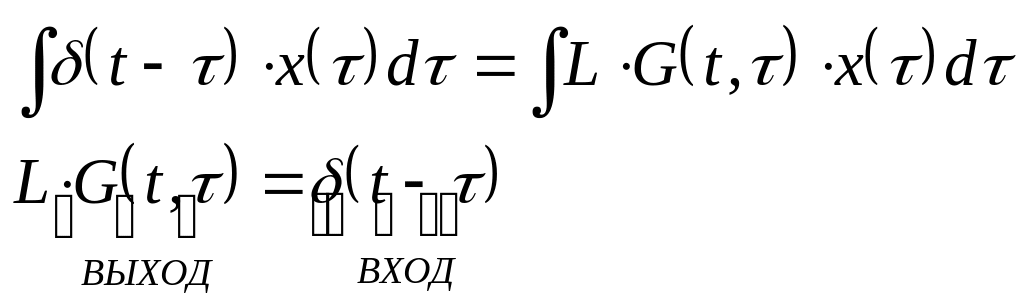(6.30.)

Из уравнения (5) вытекает очень важный факт, что ядро , которое называется функцией Грина, удовлетворяет тому же дифференциальному уравнению, если входное воздействие заменить на  - функцию.

Оказывается функция Грина имеет простой физический смысл: это отклик на единичное импульсное воздействие

Простые системы типа "вход-выход" и функция Грина

x (t) y(t)

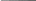
Система называется инвариантной во времени (или систем с постоянными параметрами), если входное воздействие возрождает отклик .

Если входным сигналам x₁(t) и x₂(t) соответствуют выходные сигналы y₁(t)и y₂(t)и при этом входной сигнал (а₁ и а₂ - константы) соответствует выходному сигналу - то система называется линейной.

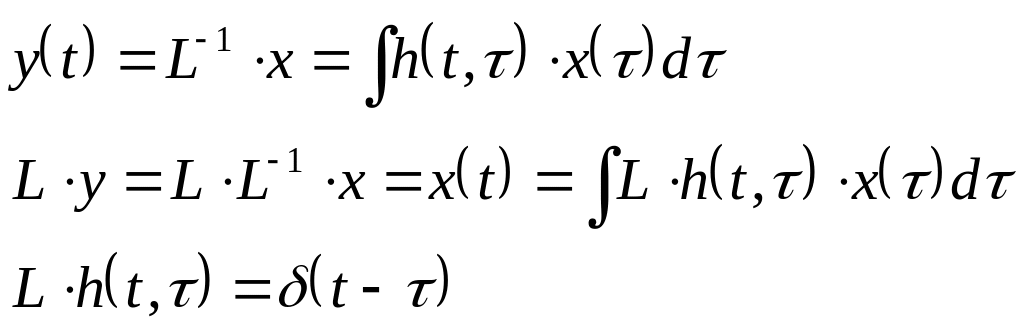
при - условие физической реализуемости.

Для стационарных систем

.