2. Символический метод расчёта цепей

синусоидального тока

Рис.3.2.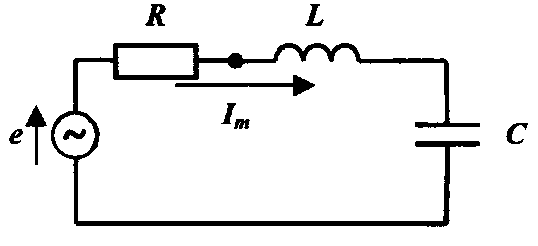

Рассмотрим схему, приведённую на рис.3.2. Генератор синусоидальной э.д.с. на электрических схемах обоз­начают в виде кружка со знаком синусоиды ~ и нанесённой рядом с ней стрелкой, показывающей направление, принятое для э.д.с. за положительное. Аналогично указывают направление переменного тока.

Составим уравнение по 2-му закону Кирхгофа:

или с учётом (1.3, 1.4, 1.5)

. (3.8)

Сущность символического метода расчёта состоит в том, что при синусоидальном токе от дифференциального уравнения (3.8), составленного для мгновенных значений, можно перейти к алгебраическому уравнению, составленному относительно комплексов тока и э.д.с.

Метод называют символическим потому, что токи, напряжения и э.д.с. заменяют их комплексными изображениями или символами: мгновенное значение тока i заменяют ком­плексной амплитудой тока , э.д.с. е – комплексом , производную заменяют на , а интеграл – на . Таким образом, дифференциальное уравнение (3.8) преобразуется в алгебраическое

, (3.9)

где – мнимая единица , а  определяется по (3.3).

На рис.3.3 дана комплексная плоскость, на которой изо­бражаются комплексные числа. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости будем откладывать действительную часть комплексного числа, а по оси ординат — мнимую часть. На оси действительных значений ставим значок +1, а на оси мнимых значений — значок +j .

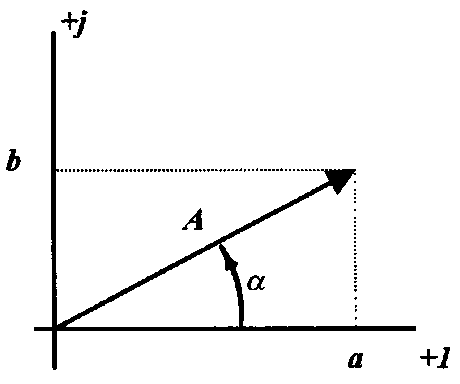Положение вектора на комплексной плоскости можно однозначно определить через его проекции на действительную и мнимую оси или через длину вектора A и угол , отсчитываемый от действи- тельной оси против часовой стрелки , т.е.

Рис.3.3.

.

Между а, b, A и  существуют следующие соотношения:

,

и

, .

Для сложения и вычитания комплексных чисел их удобно представлять в виде , а при выполнении операций умножения и деления в виде .

Вернёмся к уравнению (3.9). Сначала третье слагаемое правой части умножим и разделим на j, в результате чего получим:

.

Далее вынесем за скобки

.

Выразим

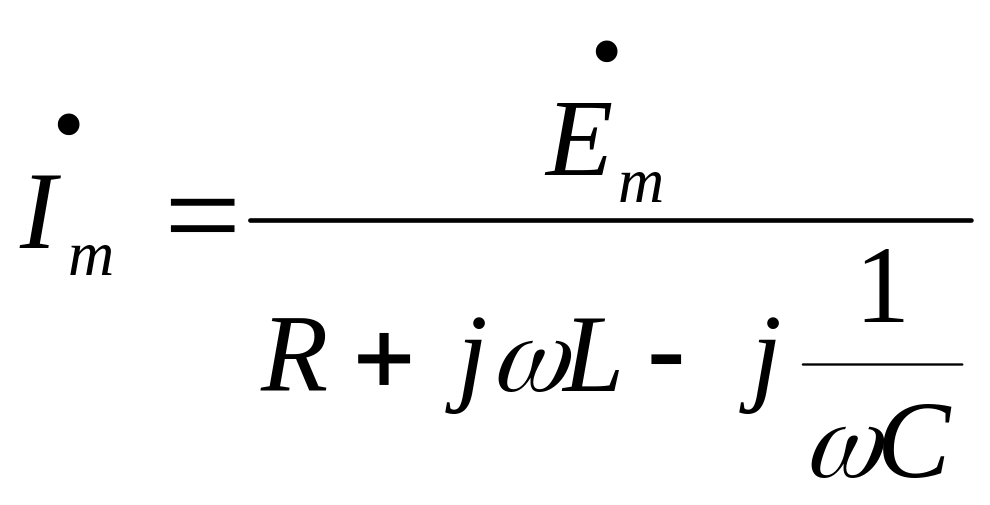. (3.10)

Выражение в знаменателе (3.10) называется комплексным сопротивлением и обозначается . Точку над не ставят, потому что принято ставить её только над такими комплексными величинами, которые являются синусоидаль­ными функциями времени. Очевидно, что резистивный элемент R в символическом методе заменяется комплексным сопротивлением R, мнимая часть которого равна нулю, индуктивный элемент L заменяется комплексным сопротивлением jL , действительная часть которого равна нулю, а ёмкостный элемент С – комплексным сопротивлением -j(1/C) , действительная часть которого также равна нулю.

Уравнение (3.10) можно записать так:

. (3.11^/)

Разделив обе части этого уравнения на перейдём от комплексных амплитуд к комплексам действующих значений

. (3.11^//)

Уравнение (3.11^/) и (3.11^//) представляет собой закон Ома для цепи синусоидального тока.

В общем случае имеет некоторую действительную часть R и некото­рую мнимую часть jX:

, (3.12)

где R – активное сопротивление;

X – реактивное сопротивление.

Для схемы рис.3.2 реактивное сопротивление

,

где X_L называется индуктивным сопротивлением [Ом], а X_C называется емкостным сопротивлением [Ом].

В том случае, когда отдельные ветви электрической цепи синусои­дального тока не связаны между собой магнитно, все расчётные формулы гл.2 пригодны и для расчёта цепей синусои­дального тока, если в этих формулах вместо посто­янного тока I подставить комплекс тока , вместо сопротивления R – комплексное сопротивление , вместо проводимости G – комплексную проводимость и вместо постоянной э.д.с. E – комплексную э д.с. .