4. Преобразование Фурье и спектральные

характеристики апериодических сигналов

Во многих отраслях техники для выявления частотных и энергетических свойств непериодических импульсов и результатов их воздействия на избирательные (резонансные) системы применяют преобразование (интеграл) Фурье.

В предыдущих параграфах было рассмотрено разложение периодических функ­ций f(t) в ряд Фурье. Такое разложение позволяет определить спектральный состав функции — амплитуды и начальные фазы её гармонических составляющих. Интеграл Фурье представляет собой предельный случай ряда Фурье для непериодической функции.

Для абсолютно интегрируемой функции в формулах прямого и обратного преобразования Лапласа можно принять р=j:

; (8.6)

. (8.7)

Формула (8.6) характеризует прямое преобразование Фурье, а формула (8.7) — обратное преобразование (интеграл) Фурье.

В формуле (8.6) предполагается, что функция f(t) задана при t>0, а при t<0 f(t)=0. Если же при t<0 f(t) отлична от нуля, то прямое преобразование Фурье имеет вид

(8.8)

и называется двусторонним.

Функция f(t) в соответствии с формулой (8.7) представляет собой сумму бесконечно большого числа гармонических составляющих. У этих составляющих в отли­чие от гармоник периодических функций амплитуды бесконечно малы, а частоты принимают все значения в диапазоне 0— . Непериодическая функция имеет непрерывный (сплошной) спектр, тогда как спектр периодической функции является дискретным.

Функцию , определяемую по соотношению (8.6) или (8.8), называют спектральной функцией, спектральной характеристикой или спектральной плотностью. Модуль F() и аргумент  функции F(j) называют соответственно амплитудной и фа­зовой спектральными характеристиками.

9. Основные понятия и модели теории электромагнитного поля

9.1. Основные понятия и определения

Если физическое состояние каждой точки в некото­ром пространстве характеризуется присущим данной точке значением той или иной векторной (или скаляр­ной) величины, то говорят, что в этом пространстве существует векторное (или скалярное) математическое поле.

Рис.9.1. Элементарный поток вектора Е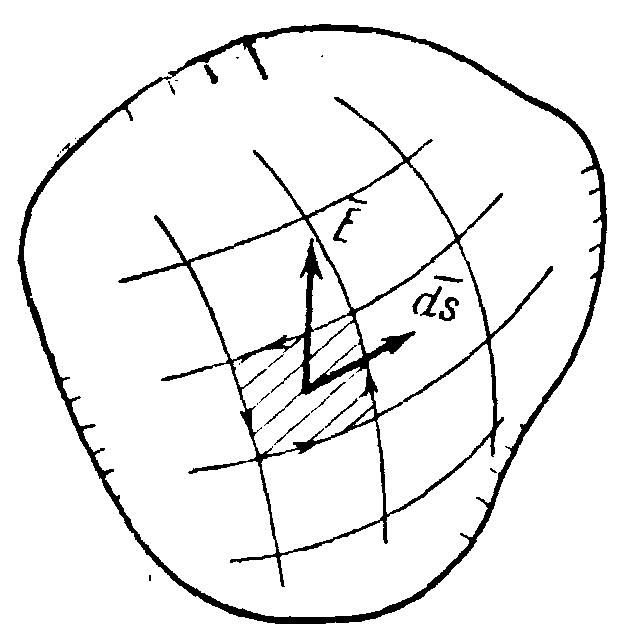

Поток вектора. Представим себе некоторый объём в пространстве, ограниченный замкнутой поверхностью. Малый элемент этой поверхности можно считать плоским и изобразить в виде вектора ds, нормального к нему. Положительное направление вектора элемента поверхности обычно свя­зывается правилом правоходового винта с направлением обхода кон­тура, ограничивающего элемент. Будем считать положи­тельным направление обхода против часовой стрелки, если смотреть на элемент поверхности снаружи (рис.9.1). Пусть рассматриваемый объём находится в поле векто­ра Е; в пределах очень малого элемента поверхности вектор Е можно считать постоянным.

Скалярное произведение Eds=Eds cos(E, ds) называется элементарным потоком вектора Е через площадку ds. Интеграл этой величины, взятый по всей поверхности, окружающей рассматриваемый объём, Eds выразит полный поток вектора, выходящий из объёма.

Поток является скалярной величиной. Вычисление потока может производиться также и через какую угодно незамкну­тую поверхность.

Рис.9.2.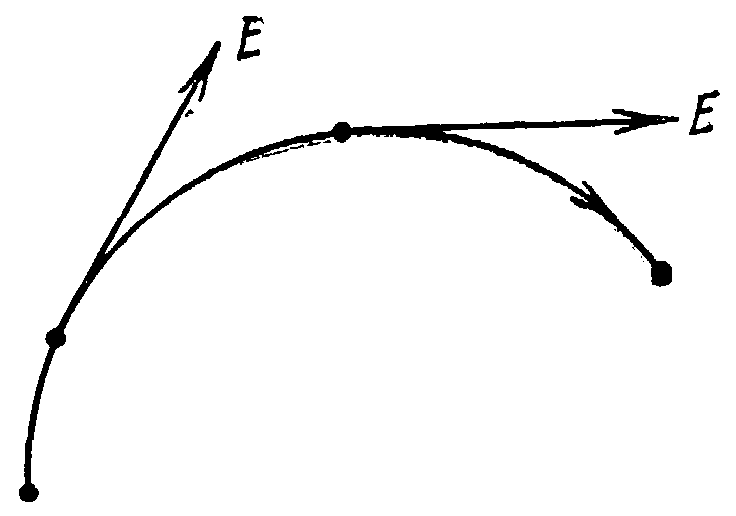

Векторное поле можно оха­рактеризовать системой линий поля, проведенных так, что век­тор в любой точке будет на­правлен по касательной к та­кой линии (рис.9.2). Такие линии называются силовыми линиями. Густота силовых линий поля может быть выбрана так, чтобы в известном масштабе соответствовать значению вектора. В таком случае поток вектора можно условно представить количеством линий поля, пронизывающих рассматриваемую поверхность.

Дивергенция вектора. Полный поток вектора через замкнутую поверхность, ограничивающую малый объём, может быть равен нулю или же отличаться от нуля.

В первом случае в объёме не содержится ни источника, ни стока (некоторого физического объекта, в котором линия поля могла бы начинаться или заканчиваться). Ограничивающая объём замкнутая поверхность может, однако, оказаться дважды пронизан­ной линией поля, идущей от источника, расположенного вне данного объема, к стоку, также находящемуся вне его.

Во втором случае внутри объёма находится либо источник, либо сток.

Предел, к которому стремится отношение полного потока вектора через замкнутую поверхность к величине ограничиваемого ею объёма при бесконечном уменьше­нии последнего, называется дивергенцией или расходи­мостью вектора

.

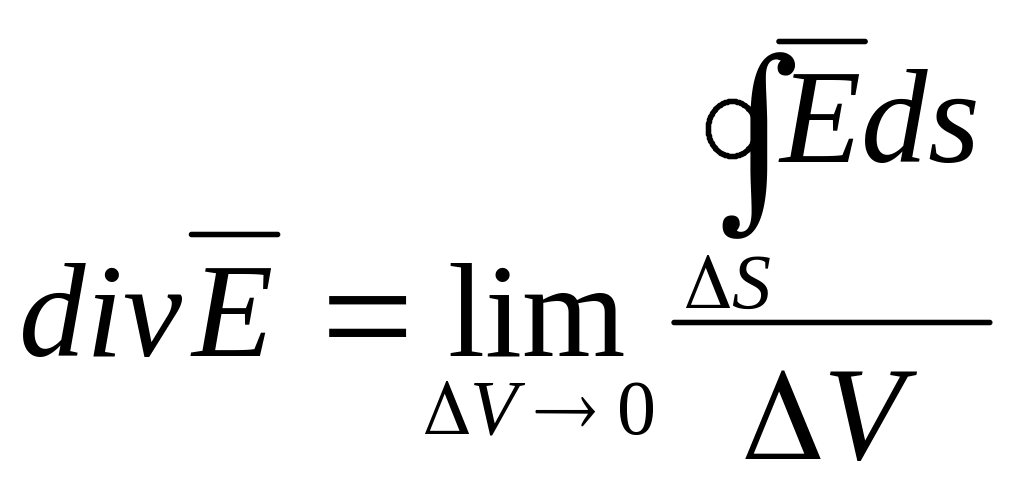Дивергенцию вектора в какой-либо точке можно условно охарактеризовать числом линий поля, начинаю­щихся или заканчивающихся в малом объеме, центриро­ванном в данной точке.

Дивергенция является скалярной величиной и она положительна, если линия поля начинается в малом объё­ме, или отрицательна, если линия поля в этом объёме заканчивается.

Ф

Рис.9.3. Дивергенция вектора скорости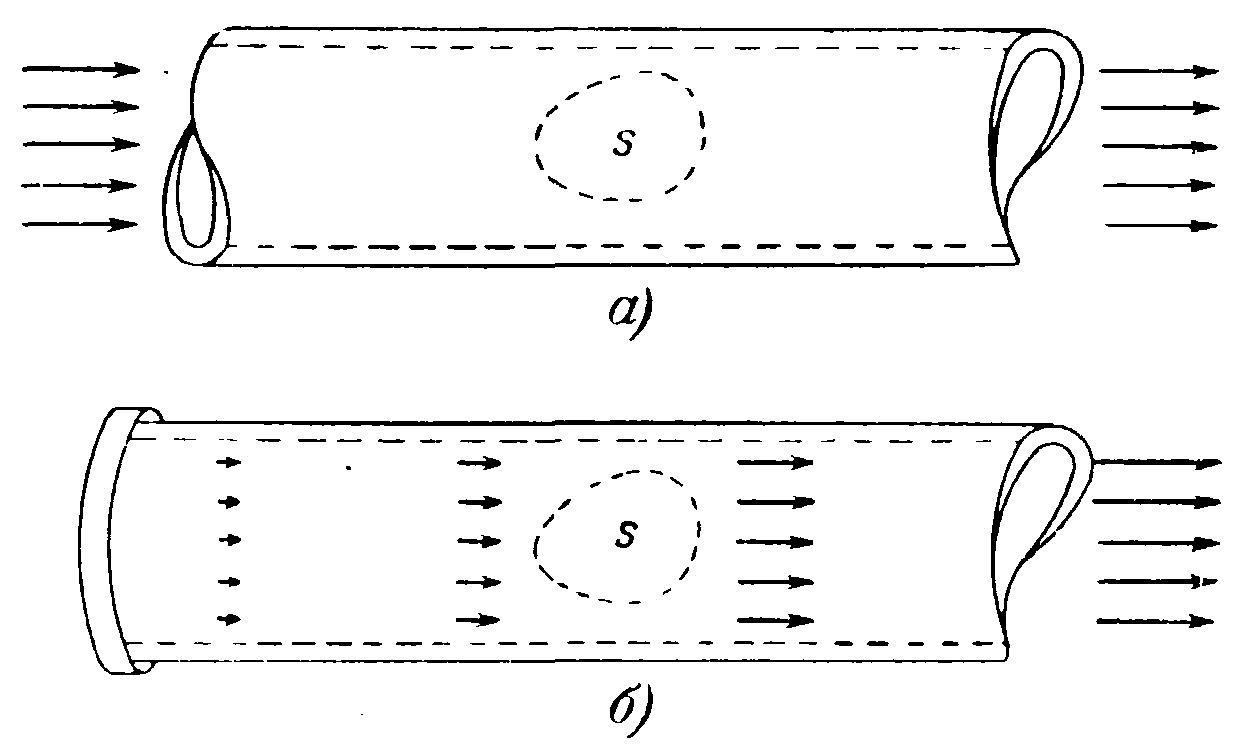

изическая сущность понятия дивергенции поясняется следующими примерами: на рис. 9.3,а показан отрезок трубы, по которой протекает вода. Рассмотрим векторное поле скорости течения воды v. Поток вектора скорости через какую-либо поверхность равен объёму жидкости, протекающей через эту поверхность в единицу времени. Поток через замкнутую поверхность s равен нулю, поскольку количество жидкости, находящейся в объёме, ограниченном такой поверхностью, неизменно. Это следует из свойства прак­тической несжимаемости воды. Следовательно, дивергенция скорости течения воды в трубе равна нулю.

На рис. 9.3,б показан отрезок трубы, закрытой с левого конца. Вначале труба была закрыта крышкой и с правого конца, а внутрь трубы накачали газ до некоторого давления выше атмосферного. Затем крышку с правого конца трубы сняли и сжатый газ стал выходить в атмосферу. Если движение газа в трубе представить векторным полем скоростей v, то дивергенция (расходимость) скорости не будет равна нулю, так как общее количество газа в каком-нибудь выделенном внутри трубы объёме s, очерченном пунктирной линией, с течением времени не остается постоянным, а уменьшается вследствие расширения газа.

Ц

Рис.9.4.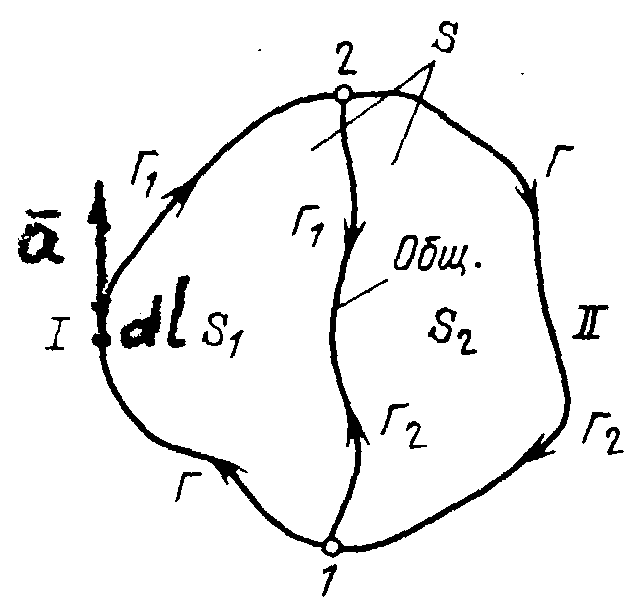

иркуляция вектора. Представим некоторую площадь S, ограниченную контуром Г, и равную сумме площадей S₁ и S₂, ограниченных контурами Г₁ и Г₂ (рис.9.4). Вектор а направлен по касательной к элементу пути dl. Циркуляцией вектора а называют величину

.

Циркуляция обладает свойством аддитивности. Это означает, что сумма циркуляции по контурам Г₁ и Г₂, равна циркуляции по контуру Г, ограничивающему поверхность S. Действительно, циркуляция C₁ по контуру, ограничивающему поверхность S₁, может быть представлена как сумма интегралов

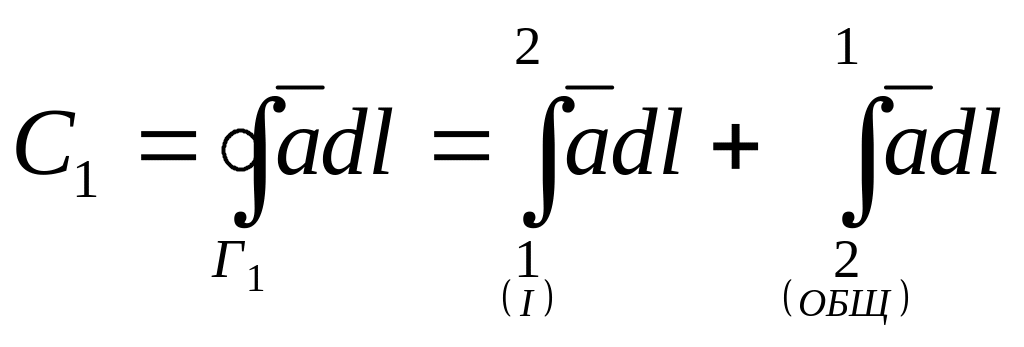. (9.1)

Первый интеграл берется по участку I внешнего контура, вто­рой — по общей границе поверхностей S₁ и S₂ в направлении 2—1. Аналогично, циркуляция С2 по контуру, ограничивающему по­верхность S2, равна

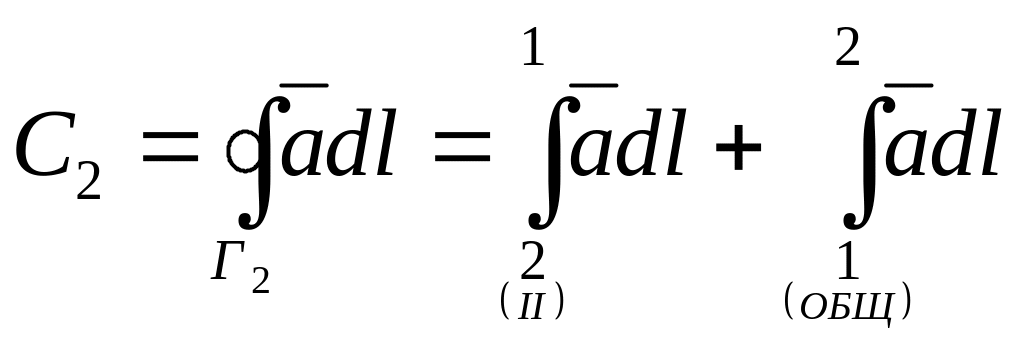. (9.2)

Первый интеграл берется по участку II внешнего контура, второй — по общей границе поверхностей S₁ и S₂ в направлении 1—2. Циркуляция по контуру, ограничивающему суммарную поверх­ность S, может быть представлена в виде

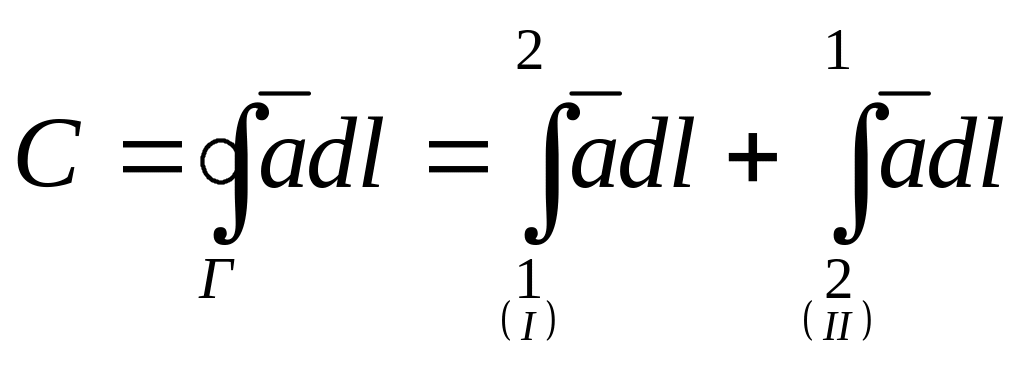. (9.3)

Вторые слагаемые в выражениях (9.1) и (9.2) отличаются только знаком. Поэтому сумма этих выражений оказывается рав­ной выражению (9.3). Таким образом,

.

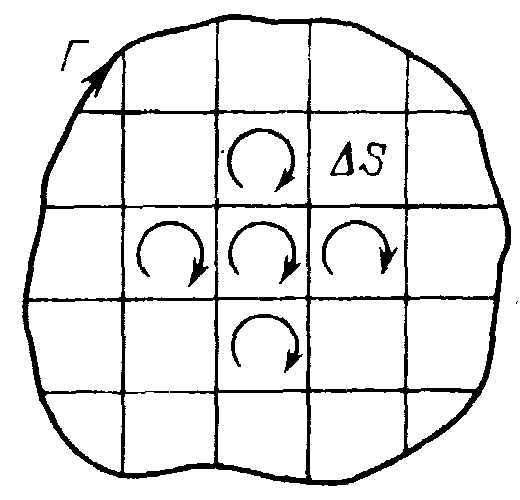
Доказанное соотношение не зависит от формы поверхностей и справедливо при любом числе слагаемых. Следовательно, если разбить произвольную поверхность S на большое число элементарных поверхностей S (рис.9.5), то циркуляция по контуру, ограничивающему S, может быть представлена как сумма элементарных циркуляции С по контурам, ограничиваю­щим S:

.

Рис.9.5.

Ротор (вихрь) вектора. Предел отношения полученной величины циркуляции к величине площадки S, при беспредельном уменьшении площадки, является вектором, который обозна­чается символом rot а и называется ротором (вихрем) вектора а

.

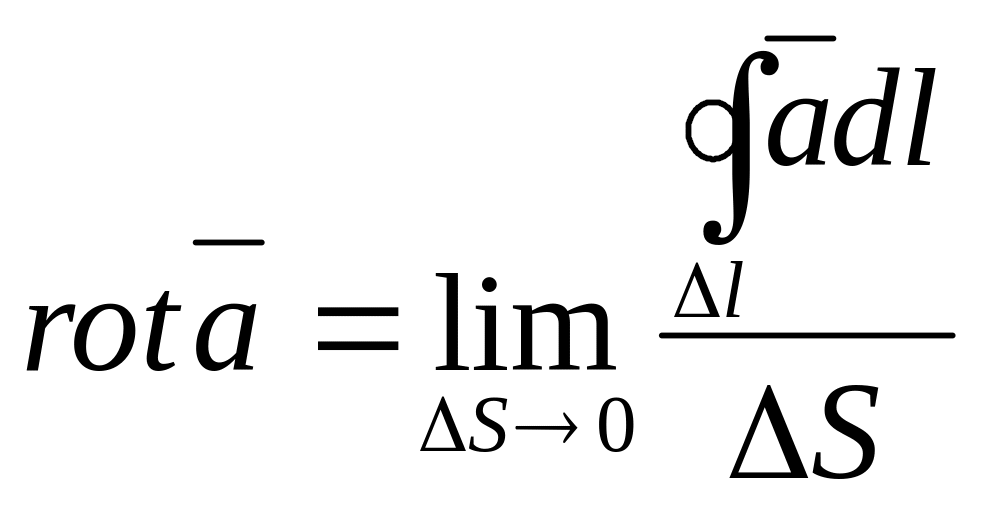Знак ротора определяется правилом правоходового винта. Если винт поворачивать в плоско­сти контура циркуляции в на­правлении, показанном на рис.9.5, то поступательное движение за плоскость чертежа бу­дет указывать направление ротора.