8. Дискретный спектр. Апериодические сигналы и их спектры

1. Гармонический анализ и разложение функций

В электротехнике, радиотехнике, технике связи очень

часто приходится иметь дело с периодическими несинусоидальными токами и напряжениями.

Они возникают в четырёх принципиально различных режимах работы электрических цепей:

1. Источник электроэнергии (источник э.д.с. или тока) несинусоидален, а все нагрузки (элементы цепи) линейны.

2. Источник электроэнергии синусоидален, а один или несколько элементов цепи нелинейны.

3. Источник электроэнергии несинусоидален и нелинейны один или несколько элементов цепи.

4. Источник электроэнергии даёт постоянную или синусоидальную э.д.с., а один или несколько элементов цепи периодически изменяются во времени.

Из курса математики известно, что любая

периодическая функция, удовлетворяющая условиям Дирихле (имеющая на конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов),

может быть представлена в виде бесконечного тригонометрического (гармонического) ряда Фурье:

, (8.1)

где А₀ – постоянная составляющая; k – номер (порядок) гармоники; А_km – амплитуда k-й гармоники; _k – начальная фаза k-й гармоники.

Таким образом, несинусоидальная периодическая функция представляет собой сумму синусоид кратных частот k = kf ( f=1/T – основная частота) со своими начальными фазами. Тот же ряд можно представить в виде сумм синусоид и косинусоид, каждая из которых имеет нулевую начальную фазу:

, (8.2)

где

; .

Гармоники, для которых k – число нечётное, называют нечётными, а для которых k – чётное, – чётными гармониками.

2. Некоторые свойства периодических кривых

К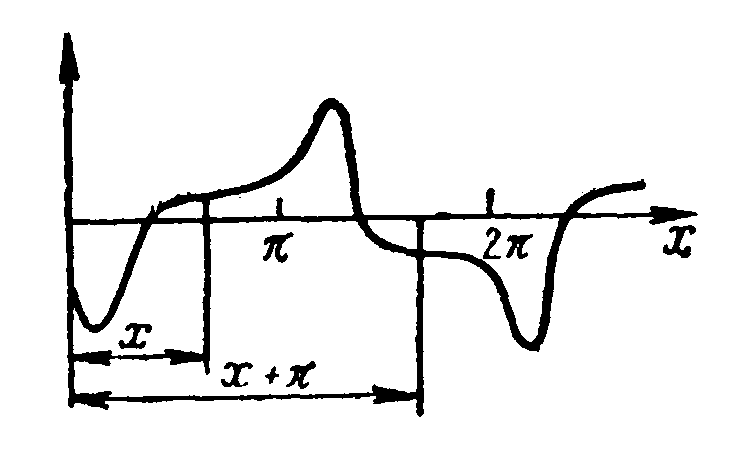 ривая на рис.8.1, удовлетворяющая условию

,

н

Рис.8.1.

азывается симметричной относительно оси абсцисс. В разложении таких кривых в ряд Фурье отсутствуют постоянная составляющая и чётные гармоники, т.е. равны нулю коэффициенты .

Кривая, подобная кривой рис.8.2, обладает симметрией относительно оси ординат. Для неё выполняется условие

Рис.8.2.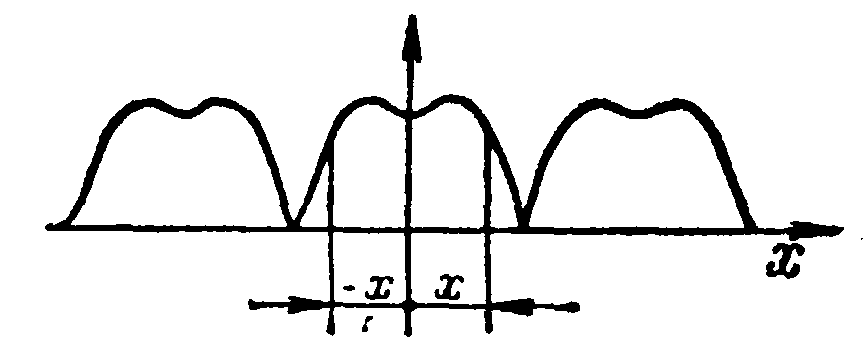

.

В разложении таких кривых в ряд Фурье отсутствуют синусные составляющие (А₁^/=А₂^/=А₃^/=…=0) и присутствуют лишь косинусные составляющие и постоянная составляющая.

Кривые по типу кривой рис.8.3 обладает свойством

.

О

Рис.8.3.

ни называются кривыми, симметричными относительно начала координат. В разложении таких кривых в ряд Фурье отсутствуют косинусные и постоянная составляющие, т.е. .

3. О разложении в ряд Фурье кривых

геометрически правиль­ной и неправильной формы.

Встреча­ющиеся в электротехнике периодические кривые могут быть раз­биты на две группы. Первая группа включает в себя периодические кривые геометрически правильной формы, например трапецеидаль­ной, треугольной, прямоугольной и т. п. Разложение их в ряд Фурье дается в таблице (см. стр.137). В ней вместо х написано t.

Вторая группа кривых включает в себя кривые произвольной (геометрически неправильной) формы (см.рис.8.1 или 8.3). Чаще всего периодические кривые второй группы задаются в виде графика. Разложение их в ряд Фурье производится графически (графоаналитически).

Графический метод определения гармоник ря­да Фурье основан на замене определенного интеграла суммой ко­нечного ч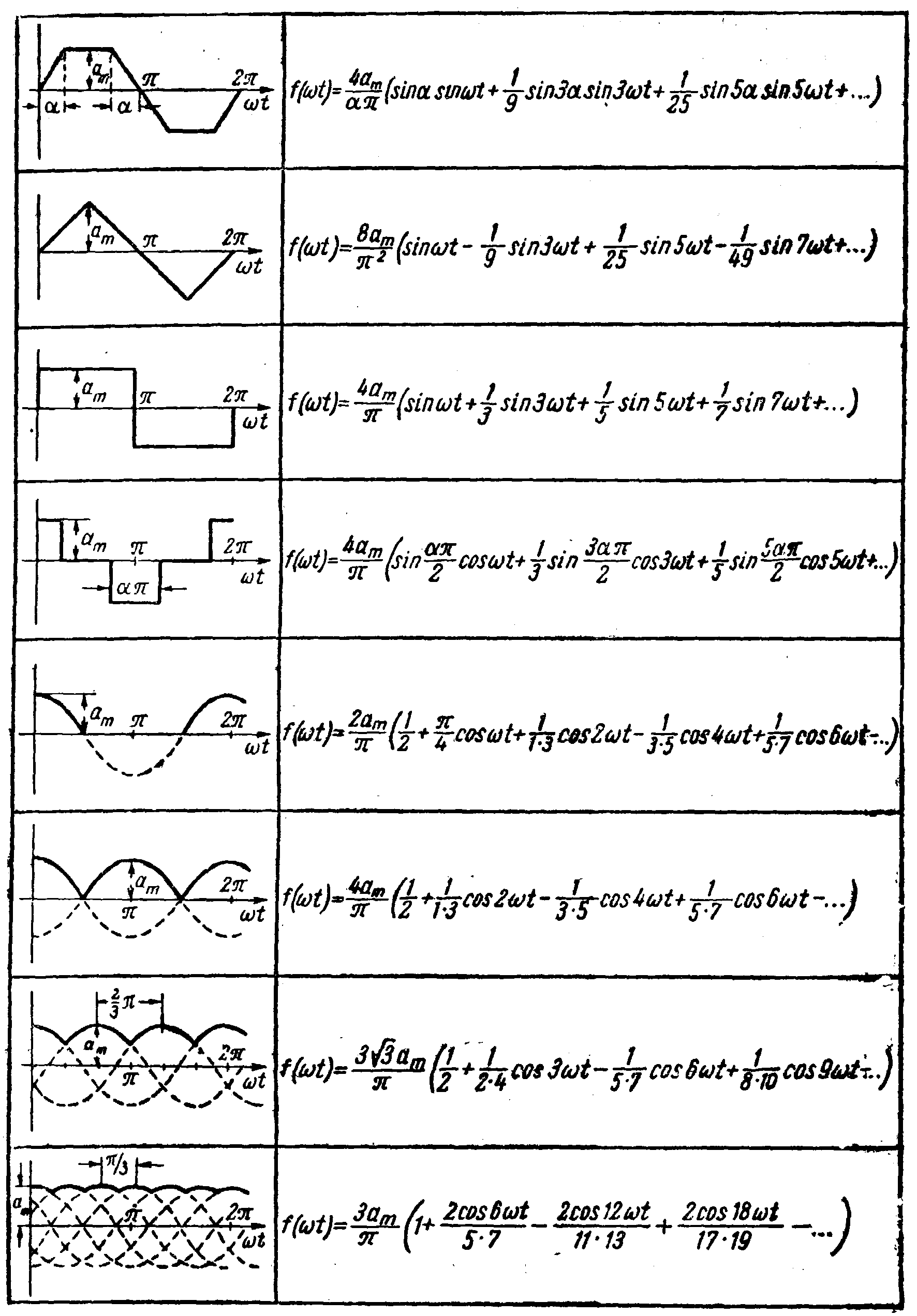 исла слагаемых. С этой целью период функции f(x), рав­ный 2 разбивают на п равных частей х

.

Тогда амплитуды гармонических составляющих будут определяться следующим образом:

постоянная составляющая

, (8.3)

где р – текущий индекс, который пробегает значения от 1 до n; f_p(x) – значение функции f(x) при значении x=px;

амплитуда синусной составляющей k-й гармоники

, (8.4)

амплитуда косинусной составляющей k-й гармоники

. (8.5)

В формулах (8.4) и (8.5) Sin_pkx и Cos_pkx – соответственно значения функций Sin kx и Cos kx при x=px.