1.4. Двухполюсные пассивные элементы

Основными двухполюсными пассивными элементами схемы являются резистивный (сопротивление или проводимость), индук­тивный и ёмкостный элементы.

Р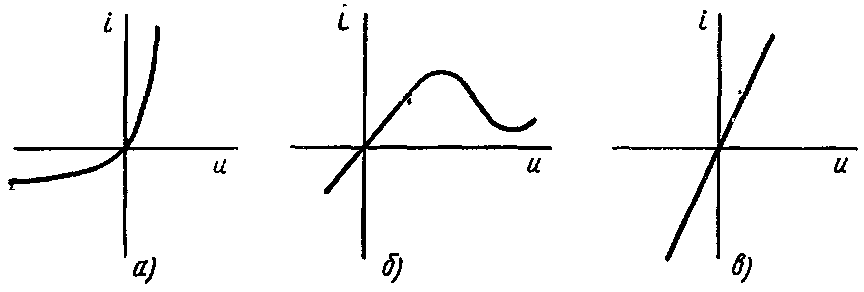 езистивный элемент. Двухполюсный элемент, характери­зуемый зависимостью u = u(i) или i(u) (см. рис.1.1,б), называют резистивным элементом — сопротивлением или проводимостью. Зависимость и(i) или i(и) называют вольт-амперной харак­теристикой такого элемента.

В

Рис.1.7. Вольт-амперные характеристики резистивных элементов

общем случае вольт-амперная характеристика нелинейна. Например, на рис.1.7,а,б показаны две нелинейные характеристики, которые могут иметь реальные элементы. Элементы с нелинейными зави­симостями и(i) или i(и) характеризуются нелинейными сопро­тивлениями или проводимостями.

Е

r(g)

сли зависимость u = u(i) представляет собой прямую линию, то сопротивление (проводимость) называют линейным (рис. 1.7, в). Обозначение такого сопротивления дано на рис.1.8.

Л

Рис.1.8.

инейное сопротивление описывается соотношением, которое носит название закона Ома:

или , (1.3)

где r – сопротивление [Ом]; g =1/r – проводимость [Сим].

Энергия, поступающая в данный элемент, преобразуется в тепловую (необратимо рассеивается). При этом мощность определяется по закону Джоуля-Ленца:

Индуктивный элемент. Двухполюсный элемент, характери­зуемый зависимостью (i) или i() (– потокосцепление), называют индуктивным элементом — индуктивностью. Зависимость (i) или i() называют вебер-амперной харак­теристикой такого элемента.. Эта характеристика может быть линейной или нелинейной. Обозначение такого элемента дано на рис.1.9.

Рис.1.9.

L

У линейной индуктивности потокосцепление линейно зависит от тока:

,

где L=const – индуктивность [Гн].

Напряжение на зажимах индуктивности возникает только при изменении потокосцепления:

. (1.4)

Ёмкостный элемент. Двухполюсный элемент, характери­зуемый зависимостью q(u) или u(q) (q– электрический заряд), называют емкостным элементом — ёмкостью. Зависимость q(u) или u(q) называют кулон-вольтной харак­теристикой такого элемента.. Эта характеристика так же может быть линейной или нелинейной. Обозначение такого элемента дано на рис.1.10.

Рис.1.10.

C

У линейной ёмкости заряд q пропорционален напряжению:

,

где С = const – ёмкость [Ф].

Ток через ёмкость протекает только при изменении заряда:

. (1.5)

2. Линейные электрические цепи постоянного тока

2.1. Закон Ома для участка цепи

Напряжение на участке цепи. Под напряжением на некотором участке электрической цепи по­нимают разность потенциалов между крайними точками этого участка.

Н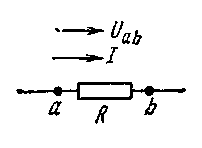 а рис.2.1 изображен участок цепи, крайние точки которого обоз­начены буквами а и b. В соответствии с определением напряжения между точками а и b:

(2.1)

П

Рис.2.1.

оложительное направление напряжения на каком-либо участке цепи (направление отсчёта этого напряжения), указываемое на рисунках стрел­кой, совпадает с положительным направлением отсчёта тока, протекающего по данному участку цепи (рис.2.1).

Закон Ома для участка цепи, не содержащего э.д.с. Пусть ток (рис.2.1) I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точки а выше потенциала точки b на величину, равную про­изведению тока I на сопротивление R:

или

(2.2)

З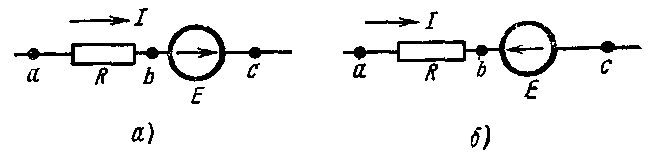 акон Ома для участка цепи, содержащей э.д.с. Этот закон позволяет найти ток участка по известной разности потенциалов на его концах и имеющейся на этом участке э.д.с. (рис.2.2).

Рис.2.2.

Для рис.2.2,а запишем потенциал точки а, пройдя от точки с:

, далее

или

,

откуда ток:

(2.3)

Для рис.2.2,б поменяется знак при э.д.с. Е:

. (2.3^/)

В общем виде можно записать:

. (2.4)

Уравнение (2.4) математически выражает закон Ома для участка цепи, содержащего э.д.с.; знак «плюс» перед Е соответствует согласованному её направлению с током (рис.2.2, а), знак «минус» — встречному (рис.2.2, б).