5.3.Простейшие схемы соединения

четырёхполюсников

Различные формы записи уравнений четырёхполюсников необходимы при вычислении уравнений сложного четырёхполюсника, составленного из двух или нескольких простых.

Рис.5.3. Последовательное соединение четырёхполюсников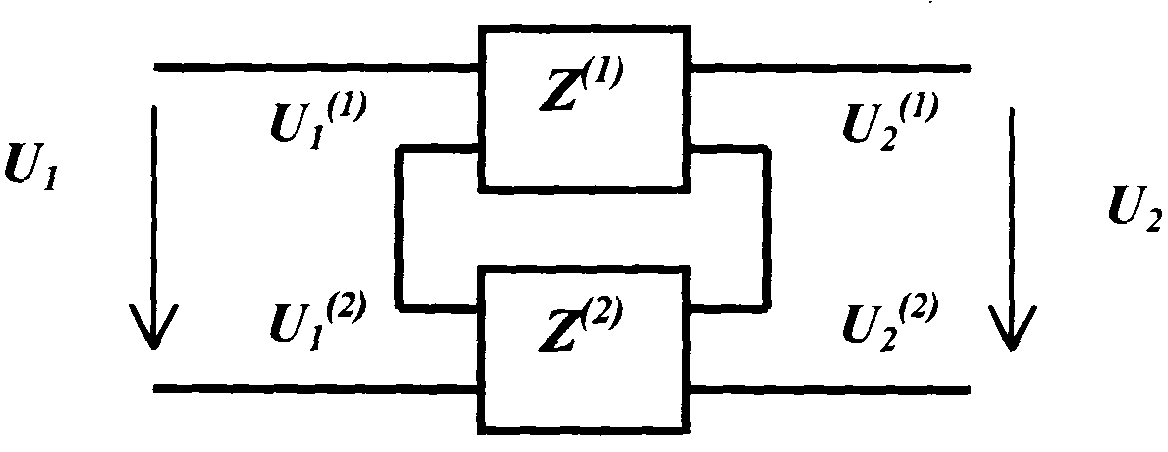

При последовательном соединении четырёх- полюсников необходимо иметь уравнения формы Z каждого из простых четырёхполюсников, так как напряжение на входе и выходе сложного четырёхполюсника равны сумме соответствующих напряжений простых (рис.5.3).

При каскадном (цепном) соединении четырёхполюсников необходимо использовать коэффициенты формы А каждого из простых (рис.5.4).

Рис.5.4. Каскадное соединение четырёхполюсников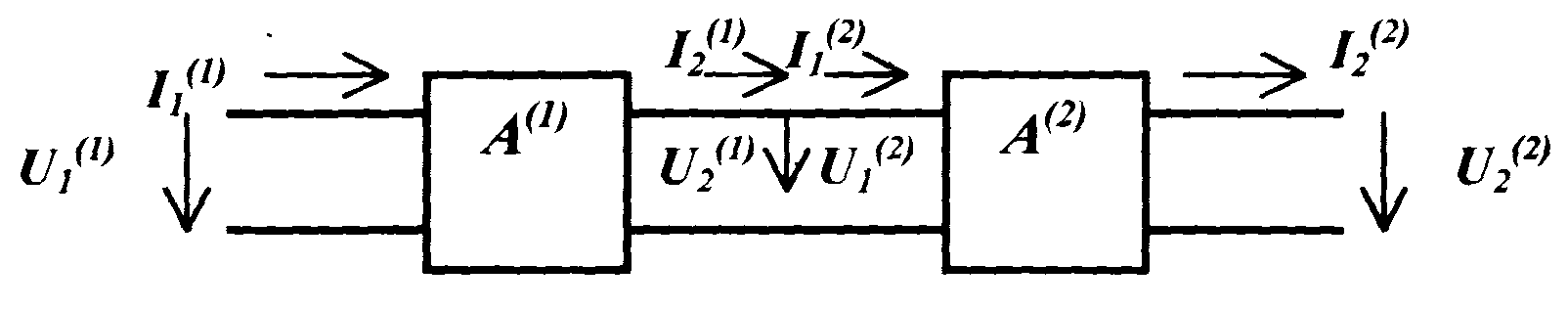

При параллельном соединении четырёхполюсников необходимо иметь коэффициенты формы Y каждого из простых, так как входные и выходные токи сложного четырёхполюсника равны сумме соответствующих токов простых (рис.5.5).

Рис.5.5. Параллельное соединение четырёхполюсников

При смешанном соединении, когда входы четырёхполюсников соединены последовательно, а выходы параллельно необходимо знать коэффициенты формы Н, так как при этом входное напряжение сложного четырёхполюсника равно сумме входных напряжений, а выходной ток сумме выходных токов простых четырёхполюсников. Аналогичная ситуация возникает при параллельном соединении входов и последовательном соединении выходов простых четырёхполюсников.

5.4. Схемы замещения четырёхполюсников

Рис.5.6. Т-образная схема замещения четырёхполюсника

Функции пассивного четырёхполюсника как передаточного звена между некоторым источником и нагрузкой могут выполнять простейшие электрические схемы – схемы замещения: трёхлучевая звезда (Т-схема) (рис.5.6) или эквивалентный ей треугольник (П-схема).

Выразим напряжение U₁ и ток I₁ на входе через напряжение U₂ и ток I₂ на выходе или, иными словами, определим коэффициенты формы А для Т-схемы.

По второму закону Кирхгофа составим уравнения для левого и правого контуров схемы на рис. 5.6:

.

Дальнейшие преобразования дают:

. (5.11)

Система (5.11) представляет собой уравнения четырёхполюсника, составленные с помощью коэффициентов формы Z. Далее выражаем ток I₁ из второго уравнения системы (5.11) и подставляем его в первое уравнение:

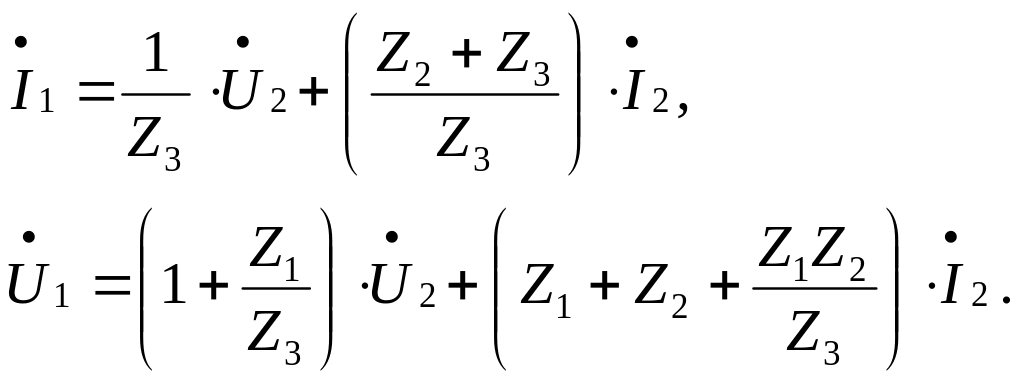
Таким образом получаем:

После простых преобразований окончательно получаем:

Читателю предлагается самостоятельно получить выражения для параметров П-схемы, используя первый и второй законы Кирхгофа.

-