1.3.2 Вторые производные термодинамических потенциалов (соотношения
Максвелла), их физический смысл
Здесь без вывода приводятся уравнения для некоторых вторых производных, имеющих большое практическое значение (см. сноску 7).
–(
)
= (
)р
=
;
(
)
= (
)Т
= –
,
где κТ – изотермическая
сжимаемость;
(
)
= – (
)т
= (
)р = α∙V, где α –
коэффициент объёмного термического
расширения.
Последнее соотношение известно как одно из соотношений Максвелла.
Вторые производные других термодинамических потенциалов пока практического интереса не представляют.
В отличие от первых производных, вторые производные определяют реальные свойства, измеряемые в независимых экспериментах (их называют термодинамическими коэффициентами). Теплоёмкость измеряется в калориметрах различной конструкции, упругость (сжимаемость) рассчитывается из упругих постоянных, находимых, к примеру, по измерениям скоростей звука, а коэффициент термического расширения находится дилатометрически. Естественно, что они чрезвычайно важны для материаловедения.
1.3.3 Фазовые переходы I и II рода.
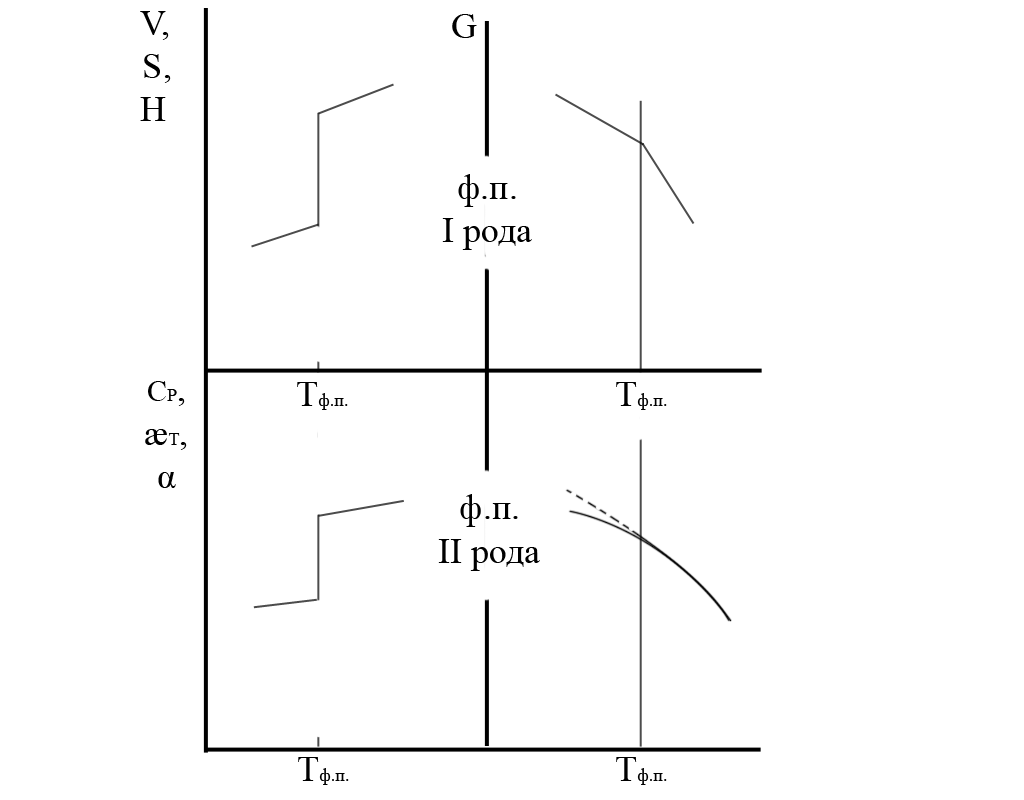
Фазовые переходы (ф.п.) I рода соответствуют фазовым равновесиям, при которых одна фаза переходит в другую при скачкообразном изменении и объема и энтропии – первых производных свободной энергии, - а также - теплосодержания. Условие равновесия соответствует тому, что обе фазы при заданных параметрах равновесия (например, давлении и температуре) могут сосуществовать одновременно сколь угодно долго. Например, кристалл сосуществует с жидкостью при температуре плавления, но плотность кристалла другая, чем плотность жидкости. Свободные энергии сосуществующих фаз равны, однако кривые пересекаются в точке перехода (см. рис. 5).
Обе фазы имеют структуры, которые не могут постепенно переходить одна в другую. При ф.п. I рода непременно претерпевают скачкообразные изменения именно первые производные термодинамического потенциала.
|
Рис. 5. Характер изменения объема (V), энтропии (S), теплосодержания(H) и свободной энергии Гиббса (G) при фазовых переходах I рода (наверху) и теплоемкости (Cp), сжимаемости (κT), и коэффициента объемного термического расширения (α) при фазовых переходах II рода (внизу). |
К этому типу переходов относятся, помимо плавления, переходы жидкость – пар, одной кристаллической модификации вещества в другую при существенном различии их структур.
Фазовые переходы II рода не соответствуют равновесию между фазами, хотя свободные энергии фаз одинаковы. Одна фаза (обычно характеризующаяся более низкой симметрией структуры) при понижении температуры постепенно изменяет параметры, характеризующие эту симметрию, и в некоторой точке эти параметры становятся соответствующими другой кристаллической структуре. Типы решеток должны соответствовать такой возможности. Области ниже точки ф.п. и выше неё отличаются разными свойствами, которым соответствуют разные величины термодинамических коэффициентов. Поэтому в точке фазовых переходов II рода непременно происходит скачкообразное изменение вторых производных термодинамических потенциалов (см. рис.44) а первые производные (объем, энтропия) изменяются непрерывно (на рисунке они не показаны). В точке ф.п. II рода кривые свободных энергии обеих фаз касаются друг друга (их энтропии одинаковы). При более низкой температуре устойчива одна фаза, при более высокой она имела бы более высокую свободную энергию или обе кривые сливались бы. Термодинамическая теория таких переходов была сформулирована П.Эренфестом в 1933 г.
К фазовым переходам II рода относят также критическую точку при переходе газ- жидкость, точку упорядочения твердых растворов9 и некоторые другие превращения. В структуре твердых растворов имеется статистическое распределение атомов в узлах кристаллической решетки, а в возникающем упорядоченном состоянии образуются фазы на основе той же структуры, но с распределением атомов разных сортов, подчиняющемся законам симметрии. Так, например, при распаде на основе твердых растворов Cu-Au происходит выделение упорядоченных фаз CuAu и Сu3Au. В теорию фазовых переходов II рода громадный вклад сделал Л.Д.Ландау (работы 1937 – 38 гг.).