6.4.2 Соотношение Максвелла для проводимости диэлектриков как основа связи

внутреннего трения и проводимости на постоянном напряжении

По существу электропроводность и механические потери - разные свойства, в которых проявляется один и тот же механизм диссипации энергии.

Свободные носители тока и вакансии структуры появляются после диссоциации структурных единиц на ионы, они смещаются по матрице стекла чтобы разрядиться на катоде (электропроводность) Энергия системы падает. При механических потерях те же изменения структуры создают возможность поглощения механической энергии, энергия системы также падает.

Предположим, что частота, входящая в уравнение электропроводности Максвелла, и частота, на которой измеряются механические потери одна и та же.

Если экспериментальные данные по температурной зависимости проводимости стекла выразить соотношением Аррениуса в логарифмическом виде

lgσ = lgσ_0эксп – ΔE_σ/2.303RT,

которое выполняется всегда в области ниже температуры стеклования, то значение температуры, при которой достигается определенное значение проводимости σ, можно получить из соотношения

T = .

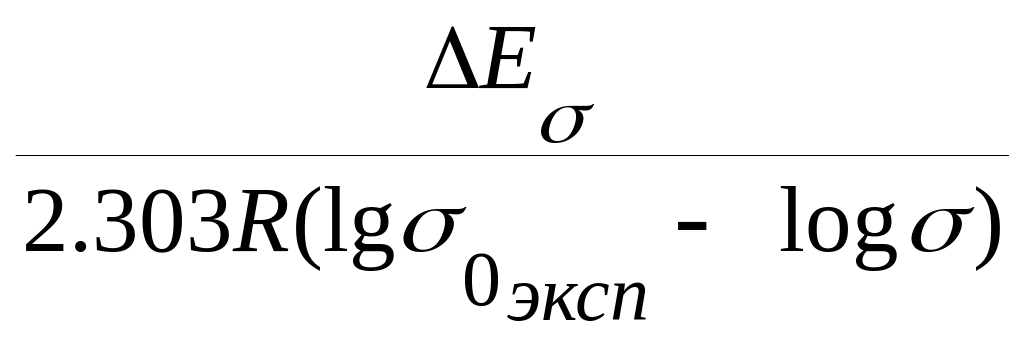Если для этого случая проводимости верно уравнение Максвелла, то

T = .

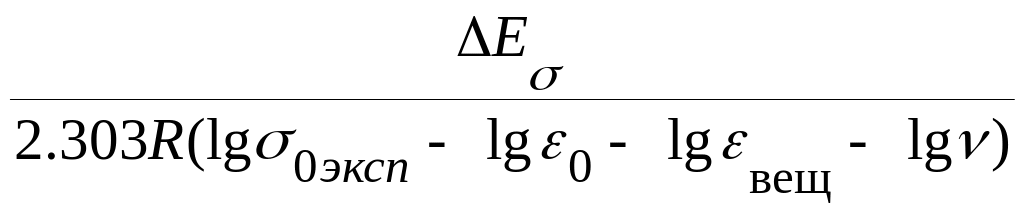Здесь ε₀ - диэлектрическая постоянная вакуума, а ε_вещ – диэлектрическая постоянная вещества, измеренная при частотах около 10¹⁰ Гц, то есть в области исчезновения заметной зависимости этой величины от частоты при ее измерениях. Поскольку мы предположили, что частота, присущая проводимости (ν =1/τ), соответствует частоте f , на которой измеряется внутреннее трение, то условие появления максимума внутреннего трения (ω = 2πf) должно соответствовать условию ω∙ν^-1 = ω∙τ = 1. Тогда уравнением для расчета температуры максимума «ионного» пика T_ион по экспериментальным данным проводимости становится соотношение

T = , (*)

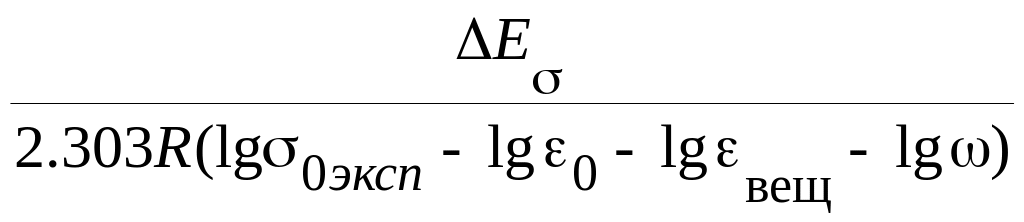где ω = 2πf. Это соотношение впервые было предложено и проверено Немиловым.

6.4.3 Экспериментальная проверка возможности расчёта температуры «ионного» максимума внутреннего трения по данным проводимости

Для проверки справедливости последнего уравнения необходимы данные по ионной проводимости стекол при постоянном напряжении, для которых имеется максимальное количество экспериментальных данных и по внутреннему трению. Эти стекла должны быть однородными (фазовое разделение в них должно отсутствовать) и их составы должны быть «типичными» для каждой стеклообразующей системы. Именно последнее обстоятельство всегда привлекает исследователей и по ним действительно число данных максимально. Кроме того, принципиально важно, чтобы максимумы внутреннего трения, приписываемые ионам, проводящим ток, были очень четко выражены в спектрах, и не было бы сомнений в их атрибуции (см. выше). По этой причине были выбраны составы однощелочных стекол, соответствующие дисиликатам R₂O∙2SiO₂ и стеклам с 20, 25 и 30 мол.% R₂O (R – Li, Na, K) ⁶⁵; было рассмотрено стекло Лилли 20Na₂O·10CaO·70SiO₂, натриево-германатное стекло 15Na₂O∙85SiO₂, одно натриево-боросиликатное стекло, борат натрия Na₂O∙2B₂O₃. а также метафосфаты лития и натрия. Для этих стекол всего были приняты в расчётах результаты всего 37 работ по внутреннему трению⁶⁶. Эксперименты проводили при разных частотах; частота f изменялась (в разных работах) в диапазоне от 0.3 до 2.4∙10³ Гц.

С целью нахождения lgσ_0эксп и ΔE_σ данные по электропроводности (измерения на постоянном токе или при частотах не более 50 Гц, когда дисперсия проводимости в пределах ошибок измерений ещё не проявляется) обрабатывались для области температур ниже Т_g по методу наименьших квадратов, если сами авторы этих цифр не приводили. Для каждого состава стекла имелось значительное количество оригинальных серий измерений, разных авторов (от 5 до 25 серий измерений для каждого состава). Эти результаты также усреднялись. Очевидно, что столь большое число экспериментальных данных позволило снизить возможность случайных ошибок, связанных с нахождением lgσ_0эксп и ΔE_σ, до минимума. Для рассмотренных стекол значения ΔE_σ находились в пределах от 59 до 86 кДж/моль, а lgσ_0эксп изменялcя от 1.6 до 2.1 (σ в Ом^-1см^-1).

Составы стекол считали совпадающими с приведенными выше, если отклонения состава изученных образцов от этих составов не превышали ± 1 мол. %.

Диэлектрические постоянные ε_вещ , измеренные при частотах 10¹⁰ Гц, рассчитывались исходя из состава по принципу аддитивности вклада в величину свойства от каждого компонента. Этот способ обобщает все существующие экспериментальные данные и позволяет рассчитывать ε_вещ с погрешностью меньшей, чем 10% от рассчитываемого значения. Источником экспериментальных данных по проводимости и внутреннему трению служила электронная база данных (SciGlass-7.0. Institute of Theoretical Chemistry, Shrewsbury, MA, 2005).

На рисунках 85-88 представлены результаты расчётов (рис. 85), и графики, демонстрирующие независимость правильности расчёта от частоты при измерениях внутреннего трения, от энергии активации проводимости, от значения предэкспоненциального сомножителя.

Рис. 85. Экспериментальная проверка уравнения (*).Соотношение Трассч и Тэкспер для однощелочных стекол.

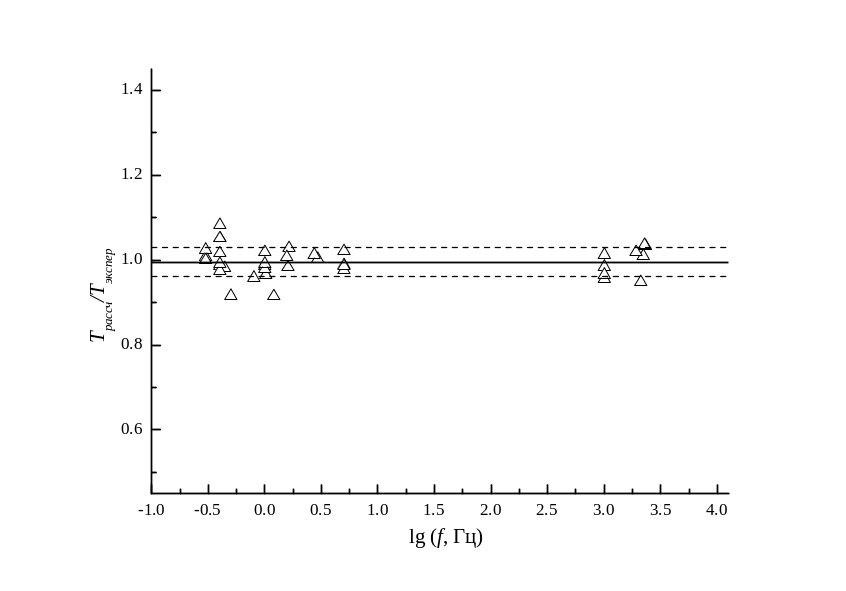
Рис. 86. Экспериментальная проверка уравнения (*). Отношение Трассч / Тэкспер для однощелочных стекол как функция частоты f .

Рис.87. Экспериментальная проверка уравнения (*). Отношение Трассч / Тэкспер для однощелочных стекол как функция энергии активации проводимости ΔЕσ.

Рис. 88. Экспериментальная проверка уравнения (*). Отношение Трассч / Тэкспер для однощелочных стекол как функция предэкспоненциального сомножителя σ0эксп.

Коэффициент достоверности корреляции для зависимости T_расч = a· T_эксп + b равен 0.956. Величины a и b составляют соответственно 0.978±0.035 и 4.822±9.899. Примечательно, что среднее значение отношения T_расч/T_эксп составляет 0.995 0.034. Это соответствует тому, что при величинах T_эксп в пределах от 260 до 400 К расхождение рассчитанных и экспериментальных величин не превышает в среднем 9 - 14 К, что находится на уровне воспроизводимости определений в эксперименте. Воспроизводимость T_эксп определена отклонениями в составе, различием режимов отжига и другими факторами. Для отожженных стекол в сравнении с закаленными экспериментальные значения T_ион по данным одних и тех же работ выше примерно на 10 К (см. [6]).

Согласно уравнению (*) рассчитанные величины T_ион наиболее существенно зависят от ΔE_σ, влияние lgσ_0эксп несколько меньше, а влияние ε_вещ совсем невелико. Последний параметр изменяется в узких пределах от 6.1 до 8.2, что при величине суммы, стоящей в скобках знаменателя уравнения (17), существенной ошибки не вносит. Однако влияние частоты f при измерениях внутреннего трения может быть чрезвычайно велико; частота в разных работах для одних и тех же составов могла изменяться в 10⁴ раз. Рис. 86 показывает, что значение отношения T_расч/T_эксп совершенно не зависит от частоты измерений, а рис. 87 и 88 подтверждают, что отношение не зависит также от ΔE_σ и lgσ_0эксп.

Таким образом, следует считать доказанной непосредственную связь между внутренним трением, имеющим релаксационную природу, и процессами ионной проводимости при постоянном напряжении, если обоснование такой взаимосвязи искать в уравнении Максвелла. С другой стороны, с большой точностью получает подтверждение само уравнение Максвелла, в котором удельную проводимость следует рассматривать также как релаксационный процесс. Найденная простая взаимосвязь между внутренним трением и проводимостью на постоянном токе до сих пор ускользала от внимания исследователей.

6.5 Эмпирические соотношения между температурами ионной, β- и α- релаксации

Обобщение всего существующего экспериментального материала по внутреннему трению неорганических стекол показывает, что существуют приближенные соотношения между температурами, соответствующими разным релаксационным процессам.

Отношение T_β/T_ion близко к 2. Это обстоятельство было известно очень давно, начиная с 60-х годов 20 века, однако удовлетворительного объяснения оно пока не находило. В работе С.В. Немилова (Физ. и химия стекла, 2010, т. 36, № 3, с. 313-349; Journ. Non-Cryst. Solids, 2011, V. 357, № 4, p. 1243-1263) показан путь решения этой проблемы, однако здесь этот вопрос не рассматривается.

Отношение T_β/T_a = 0.66±0.06. Очевидно, в оксидных стеклах β-процессы связаны со смещениями немостиковых атомов на небольшие расстояния (в пределах структурной единицы), а процессы α-релаксации обусловлены смещениями мостиковых атомов на существенно большие расстояния, соизмеримые с величиной ребра структурной единицы, если она – тетраэдр).

Отношение T_ion/T_α = 0.33 ± 0.03. Это также связано с меньшим объемом переносящих ток катионов. Однако более строгое рассмотрение теории этого соотношения здесь также опускается.

Эти соотношения следует рассматривать как полезные.

Связь ионной релаксации и структурной релаксации выражается в существовании соотношения Литтлтона, которая связывает удельную проводимость стекла σ и коэффициент вязкого течения η:

η∙σⁿ = const.

Это соотношение справедливо для очень широкого диапазона температур − от комнатной до ~1200 ºС. Значения постоянных n и const зависят от типа стеклообразующей системы и от вида катиона, переносящего ток. Теория этого соотношения долгое время отсутствовала. В работах Немилова 2011 г., упомянутых выше, показано, что значения постоянных можно рассчитать теоретически. Рассчитанные значения хорошо согласуются с экспериментом для всех типов оксидных стекол.

Смысл этой взаимосвязи в том, что мгновенный модуль сдвига определяет и свободную энергию активации и вязкого течения и свободную энергию активации электропроводности. С изменением температуры модуль изменяется, но он одинаково влияет и на вязкость и на проводимость. Условием существования соотношения Литтлтона является равенство коэффициентов объемного термического расширения всех областей структуры стекла – как областей, в которых находятся мостиковые связи, определяющие вязкое течение, так и областей, в которых находятся катионы. Это условие достаточно убедительно своей простотой.

Следует заметить, что изучение внутреннего трения с применением очень чувствительной аппаратуры позволяет выявить и существенно меньшие по амплитуде пики внутреннего трения при очень низких температурах. Обычно их относят к активированным смещениям второстепенных в структуре стекла групп (таких как, например, гидроксильные группы). Эти вопросы также находятся за рамками предлагаемого курса.