5.2.7 Ионообменные процессы с растворами. Стеклянный электрод.

Ионообменные процессы стекла с водными или другими растворами играют ключевую роль в создании стеклянных электродов, служащих для определения концентрации ионов водорода или ионов металлов. Значения pH исключительно важны во всех областях человеческой деятельности – в химической, пищевой, строительной и др. промышленностях, в медицине, в сельском хозяйстве (земледелие) и т.д.⁶³

На рис. 81 показана схема устройства стеклянного электрода. Стеклянный электрод (1) представляет стеклянную трубку (а), имеющую в торце стеклянную мембрану (б). Внутри находится раствор кислоты известной и постоянной концентрации (в) и в нём - платиновый электрод (г). При помещении стеклянного электрода в испытуемый раствор (2) ионы из этого раствора (Н⁺) обмениваются с катионами в стекле и входят в его структуру. В результате устанавливается химическое равновесие между ионами водорода в стекле и ионами водорода в испытуемом растворе. Положение равновесия определяется концентрацией ионов в растворе и в стекле. В результате этого возникает скачок потенциала между стеклом и исследуемым раствором. Его можно определить с помощью второго электрода (3) (каломельного электрода сравнения), который через электролитический мостик (4) связан с испытуемым раствором. Разность потенциалов стеклянного электрода и электрода сравнения (ЭДС, V) определена логарифмом отношения концентраций в испытуемом растворе и в растворе, находящемся внутри пузырька:

ЭДС = const + ∙ ln[H⁺].

Здесь F – число Фарадея. Постоянное слагаемое здесь определяется выбранной стандартной концентрацией, составом стекла и др. факторами. Если электрод предназначен для определения концентрации других ионов, выражение аналогично.

Принцип стеклянного электрода был известен с начала 20 в. (работы В.Нернста и др.). В исследованиях природы процессов, определяющих его функционирование, и его основного материала – стекла, большую роль сыграли работы российских учёных петербургской научной школы – Б.П.Никольского, М.М.Шульца, и многих других.

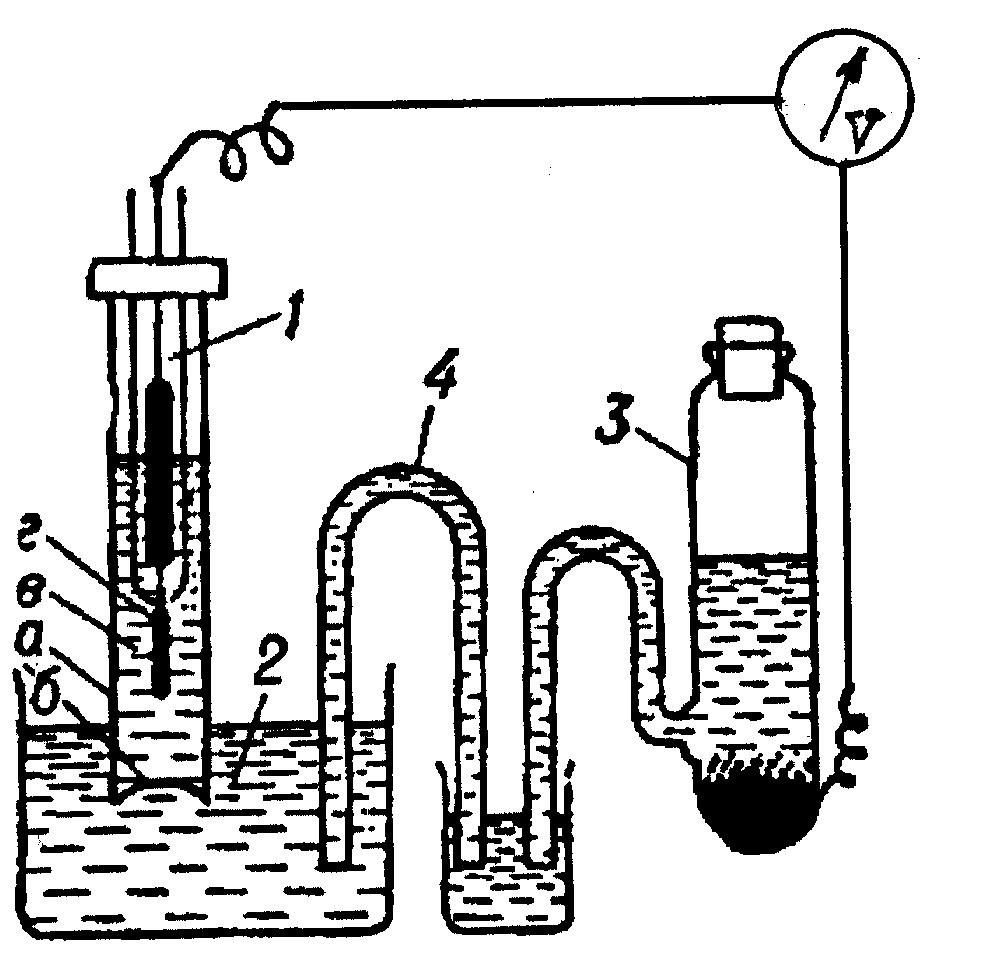
Рис. 81. Схема стеклянного электрода (пояснения в тексте).

6. Взаимосвязь между основными видами релаксационных процессов в стеклах

6.1 Основные виды релаксационных процессов в стеклах. Внутреннее трение

Внутреннее трение (механические потери при периодическом воздействии на образец) было предметом многочисленных исследований во всех странах, проводящих исследования стеклообразного состояния, начиная с конца 50-х годов прошлого века. Эксперименты такого рода обычно производят на образцах в виде нитей, которым на нижних концах сообщается периодическое закручивающее усилие (частота f). При увеличении температуры происходит поглощение усилия, если частота воздействия совпадает с частотой релаксационных процессов в образце.

При рассмотрении отклика образца на периодическое воздействие величинами, характеризующими внутреннее трение, могут быть тангенс угла потерь tgδ, где δ – угол механических потерь; λ – логарифмический декремент затухания колебаний и Q^-1, где – Q – добротность. Они соотносятся как

Q^-1 = Δ = tgδ = 2.3026 λ/π.

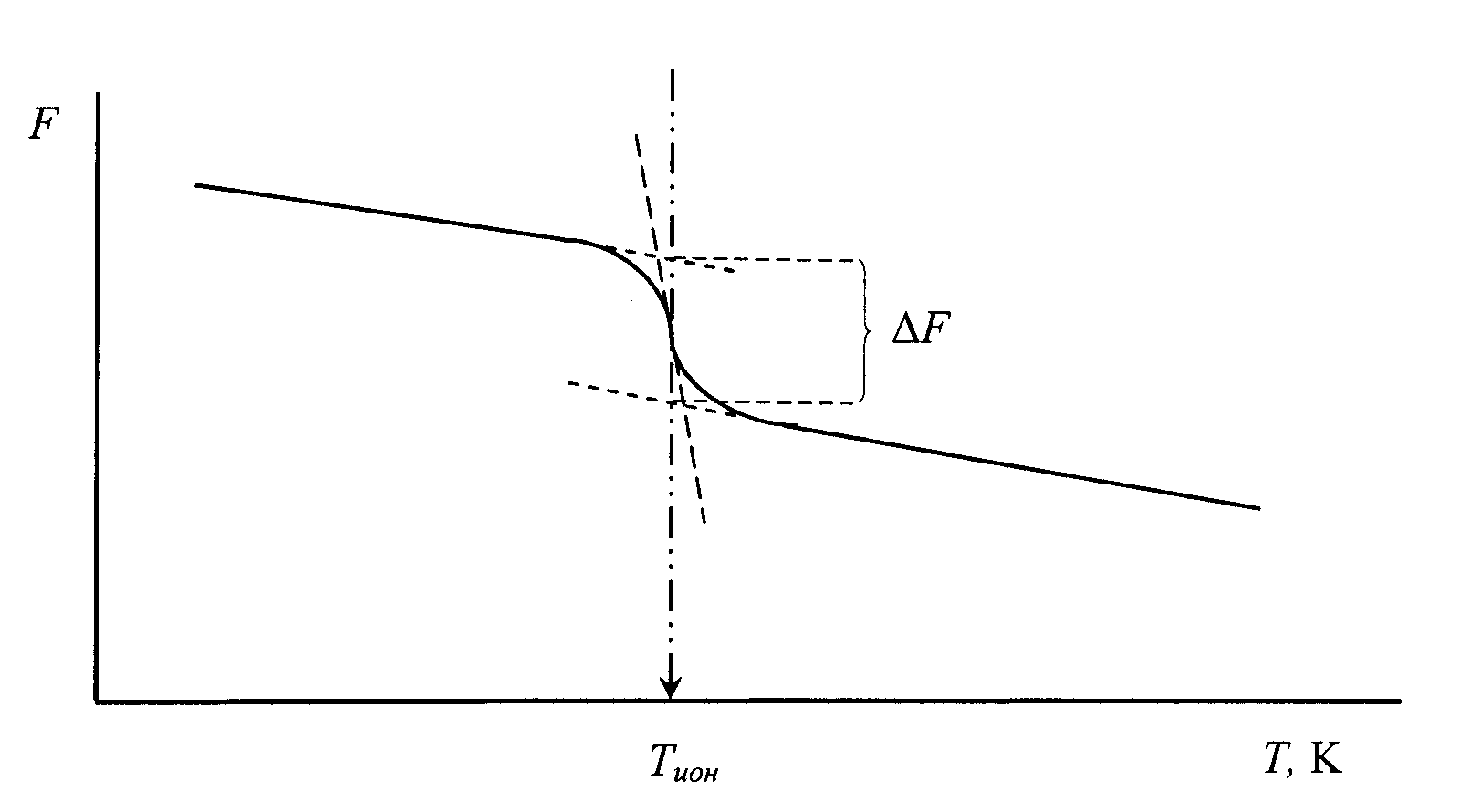
Здесь ω – угловая частота прилагаемого к образцу усилия, τ – время релаксации процесса, ответственного за поглощение механической энергии внутри образца. Сомножитель Δ определен отношением (F_∞ - F_o)/F₀, где F_∞ модуль сдвига образца при бесконечно большой частоте (реально – при столь большой частоте, выше которой модуль сдвига уже практически не изменяется), и F₀ – равновесный модуль сдвига, то есть модуль соответствующий частоте, меньше которой механическое воздействие с частотой ω поглощается. Отношение (F_∞ - F_o)/F₀ называется дефектом модуля. Эта величина наиболее просто находится из измерений модуля упругости по данным скорости распространения акустических колебаний (см. рис. 82). Условием максимума поглощения является равенство ω∙τ = 1.

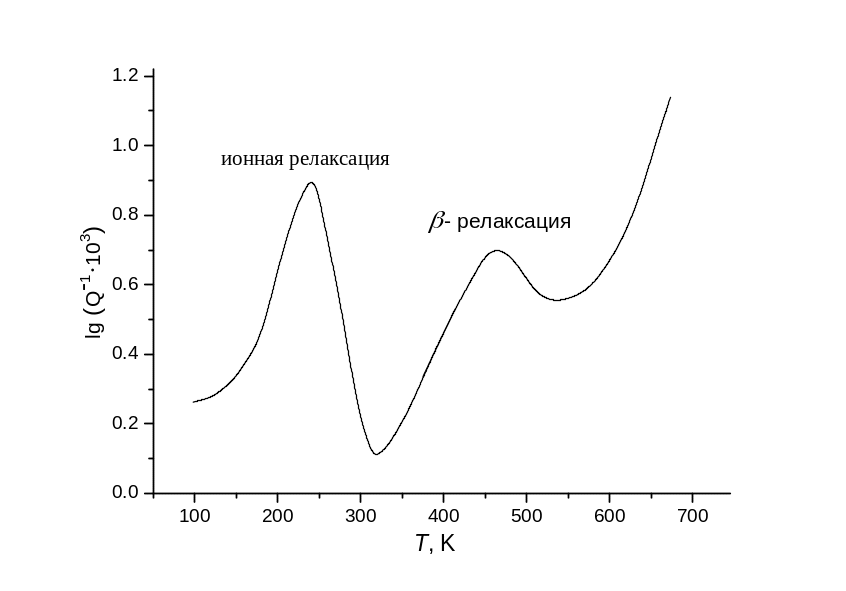
Типичная кривая температурных изменений Q^-1 (ниже температуры стеклования) для щелочно-силикатного стекла при постоянной частоте воздействия ω = 2πf приведена на

рис. 83. Здесь видны два максимума. Максимум при низких температурах («щелочной») относят к поглощению на движении свободных щелочных ионов в структуре. При использовании частот f от 0.5 до 10 Гц он расположен в области ~250 – 300 К.

Второй максимум (β-релаксация) относят к движению немостиковых атомов кислорода в структурных единицах типа ≡Si–O . Такая интерпретация является общепринятой. Однако атрибуция второго максимума в стеклах более сложного состава (содержащих помимо щелочного оксида также оксиды щелочноземельных металлов или содержащих одновременно два типа щелочных ионов) может быть неоднозначной. Второй максимум может искажаться (перекрываться) так называемым «смешанным щелочным» пиком или пиком, связанным с сопряженным движением щелочного и щелочноземельного катионов. Интерпретация деталей кривых внутреннего трения в этих случаях до сих пор остаётся весьма дискуссионной. Далее мы будем рассматривать только случаи, интерпретация которых не вызывает сомнений.

Рис. 82. Пояснение сущности возникновения дефекта модуля сдвига и положения максиму внутреннего терния на примере ионной релаксации.

Рис. 83. Максимумы внутреннего трения в стекле состава Na2O∙3SiO2; f = 0.4 Гц .

Третий максимум, при температурах более высоких чем положение максимума β-релаксации, на рисунке отсутствует. Он соответствует структурной релаксации, которая обеспечивается механизмом вязкого течения (её называют α-релаксацией). В соответствии с уравнением Максвелла, упругое механическое воздействие в этом случае поглощается полностью и производит необратимую вязкую деформацию. Поэтому правая ветвь кривой, соответствующая спаданию поглощения (правее максимума) в таком эксперименте построена быть не может. Для нахождения положения максимума α-релаксации используют составные образцы в виде сэндвичей: на поверхность тугоплавкого материала (например, кварцевого стекла или сапфира) наносят слой изучаемого стекла. Тогда поглощение всего образца при α-релаксации изучаемого стекла не гасится полностью – остаётся фон от подложки и дефект модуля позволяет найти положение температуры максимума α-релаксации изучаемого стекла, аналогично графику рис. 82.

6.2 Расчёт температур максимума α-релаксации на основании уравнения Максвелла

Уравнение Максвелла имеет вид

F_∞· τ_M = η.

Мгновенный модуль сдвига F_∞, получаемый при 298 K, может отличаться от модуля сдвига F_∞, соответствующего T_g , лишь незначительно (не боле 3-5 %), поскольку температурный коэффициент модуля ниже температуры стеклования очень мал. Время релаксации Максвелла τ_M является критерием перехода в твердоподобное состояние (в стекло). Условие ν∙τ_M =1, где ν = частота внешнего воздействия на систему, позволяет найти коэффициент ньютоновской вязкости, который соответствует T_α. Поэтому мы в состоянии найти T_α, основываясь на частоте f и значении модуля при комнатной температуре F_∞, если известна экспериментальная зависимость logη от температуры. Таблица подтверждает правильность таких расчётов. Отношение рассчитанных T_α к измеренным составляет 1.0080.016.

Таблица. Сопоставление значений T_α, рассчитанных по уравнению Максвелла и экспериментально найденных по изучению внутреннего трения.

Состав стекла	f , Гц	F∞, ГПа , 298 K	log(η, Па∙с)	Tα, К
				Раcсчитано	Эксперимент
SiO2*)	0.8	31.5	10.59	155315	1511
Оконное стекло**)	1	27.4	10.44	8665	876
Оконное стекло**)	1	27.4	10.44	8665	861
Оконное стекло**)	0.005	27.4	12.74	8145	805
25Na2O∙75SiO2	0.3	24.2	10.91	7606	770
25Na2O∙75SiO2	1	24.2	10.38	7736	783
33Na2O∙67SiO2	5)	24.5	9.69	7659	757
20K2O∙80SiO2	0.3	19.8	10.81	7997	776
20K2O∙80SiO2	1	19.8	10.29	8137	792

^*) Получено плавлением природного бразильского кварца в кислородно-водородном пламени. Вязкость соответствует именно такому способу получения стекла.

^**)14.76Na₂O;0.45K₂O;6.7CaO;4.14MgO;1.84Al₂O₃;71.54SiO₂; 0.11Fe₂O₃;0.46SO₃ (мол..%, по анализу).

6.3 Релаксационные процессы β-типа, их природа и значение

Как упоминалось, этот максимум соответствует движению немостиковых атомов кислорода. К сожалению, о его природе более ничего не известно, поэтому использовать уравнение Максвелла для расчёта температур его положения сегодня нельзя.

Однако в разделе «Физическое старение стекла при комнатной температуре» упоминалось, что частоты релаксации, соответствующие различным каналам релаксационного процесса старения, соответствуют именно этому виду релаксации.

Если общее выражение для времени релаксации для набора каналов старения записывается как

lgτ_i = γ_i×T_13.5 + b,

то для каждого канала по значениям γ_i можно рассчитать величины свободных энергий активации ∆G_i^≠ для каждого канала. Поскольку универсальное значение слагаемого b соответствует классическому значению предэкспоненциального сомножителя в уравнении для частоты релаксации (lg(τ_i^-1) = 13 при выражении времени в с), то

для каждого канала по уравнению

lg(τ_i^-1) = 13 − ∆G_i^≠/2.3RT_i

можно рассчитать значение температуры T_i, при которой эта частота (τ_i^-1) будет соответствовать частоте f.

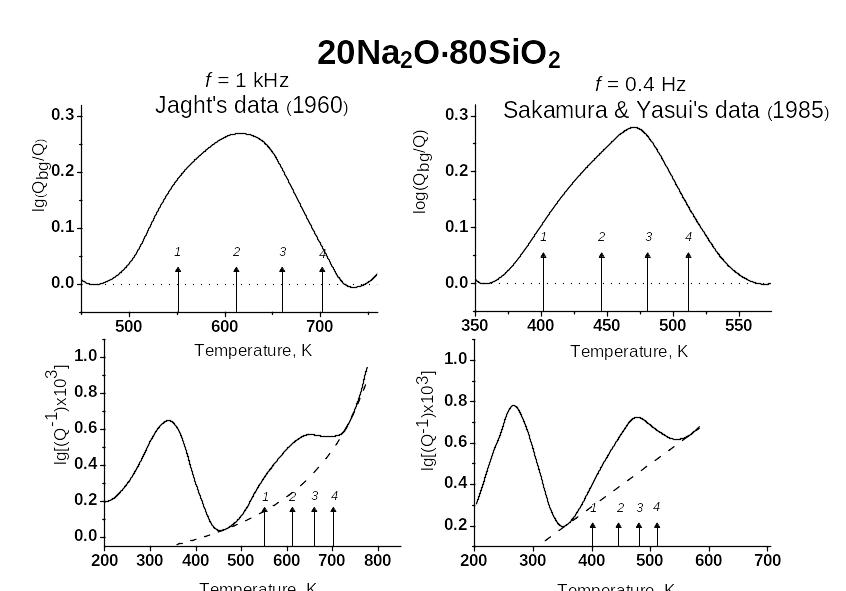
Оказывается, что эти температуры точно вписываются в максимум внутреннего трения, соответствующий β-релаксации (пример – на рис. 84).

Рис. 84. Положение температур, соответствующих релаксационным каналам старения (с 1 по 4) для стекла 20 Na2O∙80SiO2 при двух частотах по данным разных авторов. В нижней части рисунков показана общая картина внутреннего трения , включающая (слева) «ионный» максимум. (S.V.Nemilov, Glass Sci. and Technol. v.78, No 6, 269-278, 2005).

Таким образом, предположение что старение стекол при комнатной температуре обусловлено небольшими смещениями немостиковых атомов кислорода, совершенно оправдано.

6.4 Ионный максимум и связь внутреннего трения с проводимостью на

основании теории Максвелла

Ионный максимум, находящийся в области ~230 - 450 К (в зависимости от частоты эксперимента), изначально связывали со смещениями ионов, ответственных за ионную проводимость при постоянном напряжении. Основанием было совпадение энергий активации проводимости и энергии активации внутреннего трения, если энергии активации последнего вида релаксации рассчитывать на основании обычной аррениусовской зависимости как коэффициент ΔE

f = f₀ ∙exp( - ΔE/RT).

Доказательство справедливости этого отождествления с привлечением теории Максвелла было недавно дано С.В. Немиловым (Journ. Non-Cryst. Solids, 2011, V. 357, № 4, p. 1243-1263 2011; Фиика. и химия стекла, 2012, т. 38, № 1, с. 39-57; Glass Phys. and Chem. 2012, vol.38 No1, pp. 27-40)⁶⁴.