5.2.6 Ионообменные процессы и проблемы современной оптической технологии

Принцип формирования профиля показателя преломления в элементах градиентной оптики⁶²

Элементы градиентной оптики (граданы) представляют собой оптические детали, в которых существует градиент показателя преломления, созданный искусственным путём за счет наведения градиента концентрации. Например, если стекло, в состав которого входит оксид щелочного металла, поместить в контакт с расплавом соли, содержащим другие ионы того же заряда, то между стеклом и расплавом начнет происходить обмен ионами. Ионы из стекла будут переходить в расплав (их там нет и существует движущая сила процесса – разность химических потенциалов) и из расплава ионы будут входить в стекло, замещая вышедшие ионы:

Na⁺(стекло) + KNO₃ (расплав) ↔ K⁺ (стекло) + NaNO₃ (расплав).

Распространение чужеродного иона в стекле от поверхности вглубь определяется процессами диффузии. Возникающее распределение концентрации будет постепенным – на поверхности замещение максимальное. Состав поверхностного слоя и концентрация входящего иона на поверхности, задаваемая составом соляного расплава, определяет его диффузию иона внутрь образца. При этом ионы, находящиеся в объеме и выходящие на поверхность, будут обмениваться местами с ионами, входящими в объем (диффузантами), этот процесс характеризуется коэффициентом взаимодиффузии. Процесс взаимодиффузии отличается от процесса самодиффузии, при котором ион входит в стекло с поверхности, но встречного потока нет.

Для выбора состава стекла, состава соляного расплава и параметров технологического режима (температуры, времени), необходимых для достижения требуемого профиля показателя преломления, нужно знать природу таких процессов и уметь математически моделировать результат всей процедуры. При этом важны многие обстоятельства, о которых мы здесь только упомянем, поскольку вся проблема могла бы составить предмет специального курса.

Рис. 78. Функции erf(z) и erfc (z), используемые при программировании изменения свойств в процессе ионного обмена.

Следует помнить, что линейная связь показателя преломления и концентрации существует не всегда. Это – некоторый идеальный случай. Знание реального концентрационного профиля при ионном обмене первостепенно по своей важности.

Наиболее прост идеальный - линейный - случай, когда коэффициент диффузии не зависит от концентрации диффузанта. Практически он никогда не реализуется. В этом случае профиль концентрации при диффузии в полубесконечную пластину должен соответствовать erfc- фунцкии от аргумента

z = x(4Dt)^-1/2,

где х – координата, t – время, D – коэффициент диффузии. Сама erfc(z) = 1 – erf(z), где erf(z) = 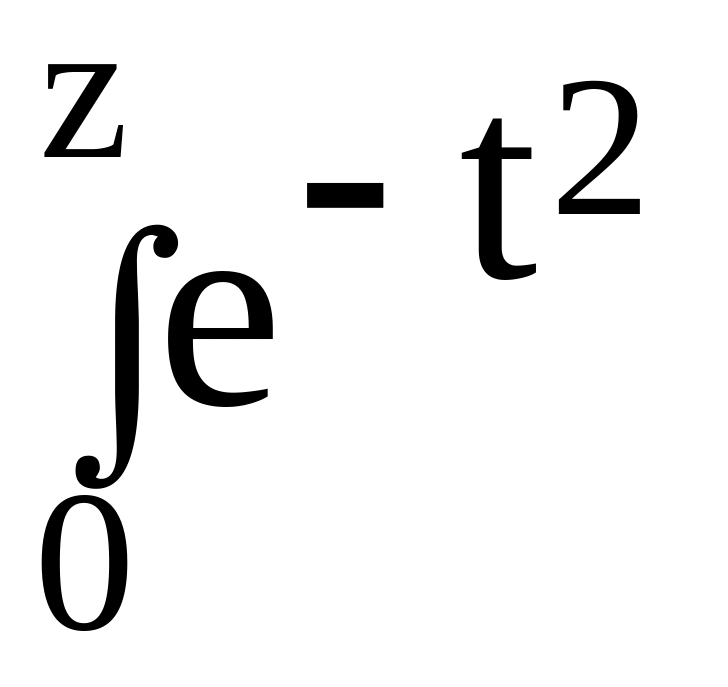dt есть функция Лапласа (функция ошибок). Она табулирована и ее значения (меняющиеся плавно) можно найти в математических справочниках. Изменение этих функций от z показано на рис. 78. Здесь нужно заметить, что использование приведенных выше функций имеет совершенно ясный смысл в описании возникновения профиля показателя преломления, поскольку законы Фика определяют коэффициент диффузии как характеристику распределения именно концентрации в образце. Важно только, постоянен ли коэффициент диффузии в зависимости от концентрации.

Особенности ионообменных процессов между стеклами и расплавами солей

В реальных случаях коэффициент диффузии всегда зависти от концентрации.

Показатель преломления уменьшается от поверхности вглубь образца, если диффундирует катион, сообщающий стеклу больший показатель преломления, чем показатель исходного стекла. Профиль показателя преломления, если он не очень глубок (<150 мкм) экспериментально устанавливается по результатам измерения модовых спектров плоских оптических волноводов, полученных для каждого стекла заданного состава в результате ионного обмена.

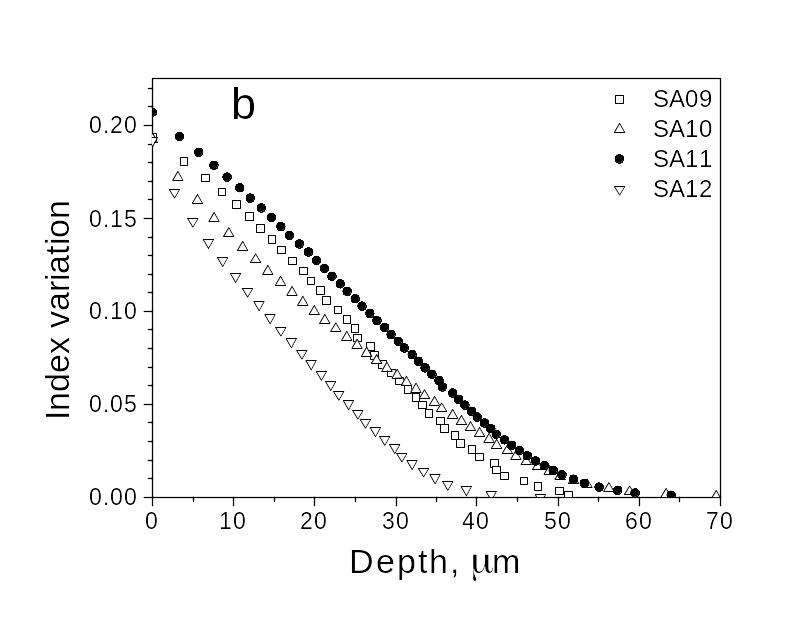
Рис. 79. Изменение показателя преломления от глубины проникновения диффузанта с поверхности. Эксперимент для образцов, отличающихся составом.

На рис.79 показан пример распределения показателя преломления (для длины волны λ = 0.63 мкм) по глубине (от поверхности вглубь) для нескольких близких составов стекол (диффузант – ион Ag⁺).

Для глубоких профилей используются интерферометрические или рефрактометрические методы.

Соответствующий этим профилям показателя профиль коэффициента диффузии D поучается математической обработкой с применением поясненных выше функций.

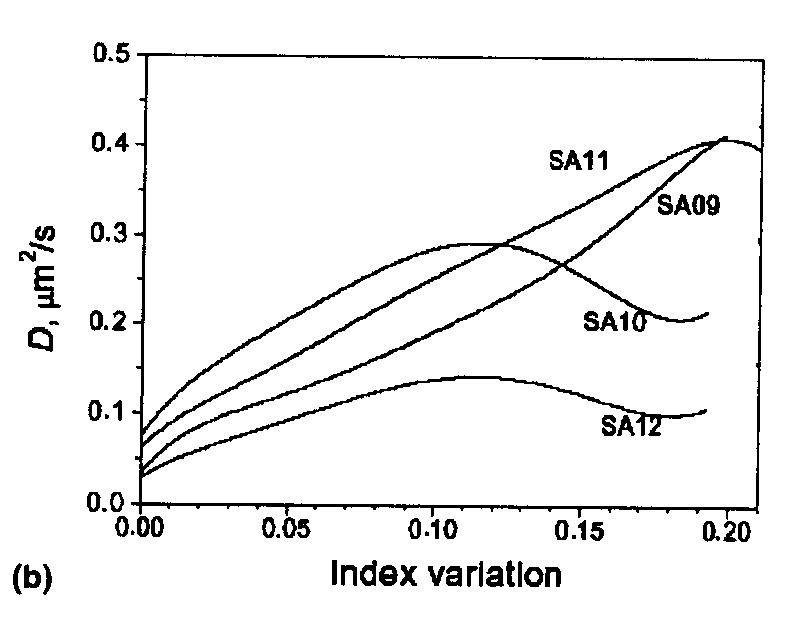
Рис. 80. Изменение рассчитанного эффективного коэффициента диффузии от показателя преломления в профиле показателя, представленного на рис.79.

При этом полагается, что закон Фика справедлив, но коэффициент диффузии непостоянен. Эти результаты приведены на рис. 80.

Естественно, что от поверхности «вглубь» образца изменяется концентрация диффузанта и коэффициент диффузии меняется с этой концентрацией. Одна из причин зависимости D от концентрации (которая существует всегда) может быть пояснена строгим рассмотрением совокупности противоположно направленных ионных потоков от поверхности «внутрь» образца и «изнутри» к поверхности. Это рассмотрение основано на принципах неравновесной термодинамики (используется соотношение Онзагера).

Если концентрации ионов сортов А и В обозначены как с₁ и с₂ соответственно и с₁ + с₂ = 1, то коэффициент взаимодиффузии D определен уравнением

D =

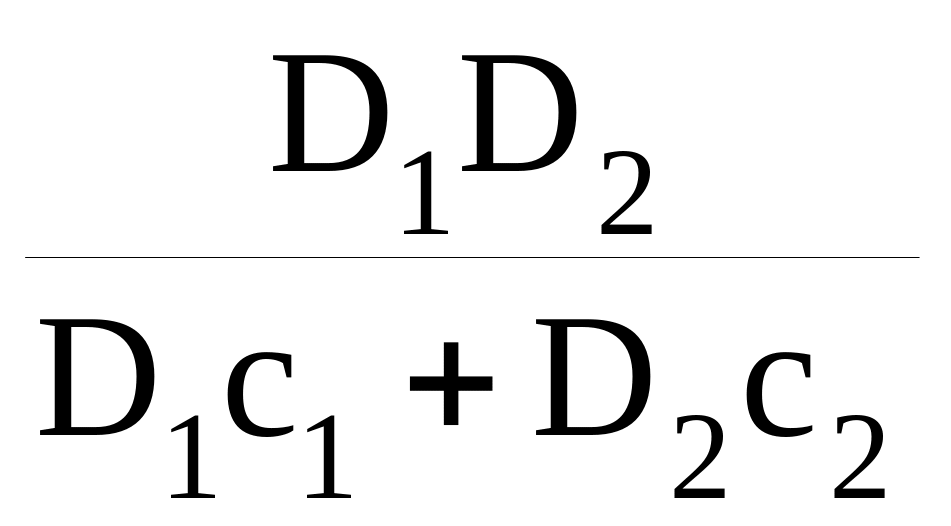
Таким образом, зависимость D от коэффициентов самодиффузии ионов D₁ и D₂ изначально предопределяет нелинейную зависимость D от концентрации.

Другие причины появления нелинейности состоят в том, что при ионном обмене могут возникать внутренние напряжения из-за того, что «новый» ион входит в структуру стекла, не соответствующую размеру этого иона. Сами напряжения существенно влияют на коэффициент диффузии и на функцию распределения концентрации. Напряжения изменяют как рефракцию иона, так и рефракцию атомов кислорода в его окружении. Возможность «подстраивания» структуры к диффундирующему иону характеризуется отношением

Ф = τ_d/τ_α,

где τ_d - характеристическое время диффузии, а τ_α– характеристическое время релаксации структуры. Математический анализ показывает, что закон Фика работает либо при Ф < 0.001, либо при Ф > 100 000. Это соответствует температурам ионного обмена либо ниже, либо выше Т_g примерно на 200 – 300 К.

Выбор температуры ионного обмена очень важен прежде всего для создания абсолютной величины перепада показателя. Если ионы Ag⁺ в принципе (как одни из самых поляризуемых) способны создавать очень высокий прирост показателя, то условия проведения ионного обмена при Т < Т_g позволяют достичь значений прироста показателя около 0.2. Это очень высокие значения, не реализуемые в других условиях.

Профиль концентрации и функция градана как элемента оптической системы зависят также от формы первоначального образца, подвергаемого ионному обмену (пластина, цилиндр, шар). Например, градан в виде пластины может заменить цилиндрическую линзу, градан в виде цилиндра может заменить сферическую линзу и т.д. Все эти случаи исследовались теоретически и экспериментально. В настоящее время найдены математические методы расчета, позволяющие получать заданный профиль показателя преломления соответственно предполагаемому использованию получаемой оптической детали.

При проникновении из расплава внутрь цилиндрического образца иона с высокой поляризуемостью возникает «отрицательная» линза. Её можно перевести в «положительную» линзу, если образец, полностью проработанный до середины, вновь поместить в соляной расплав с ионом низкой поляризуемости. Такие «ванны» можно менять по нескольку раз для достижения нужного профиля показателя.

При всей сложности проблемы для получения образца с заданными оптическими характеристиками все технологические параметры процесса ионного обмена рассчитываются математически с необходимой точностью с использованием компьютерной техники.

Размер деталей градиентной оптики может быть практически любым, минимальные диаметры линз имеют порядок 0.1 см.

При обработке стекла кислотой или водными растворами щелочные ионы замещаются на протоны (Н⁺). Однако для практических целей такие процессы большого интереса не представляют.