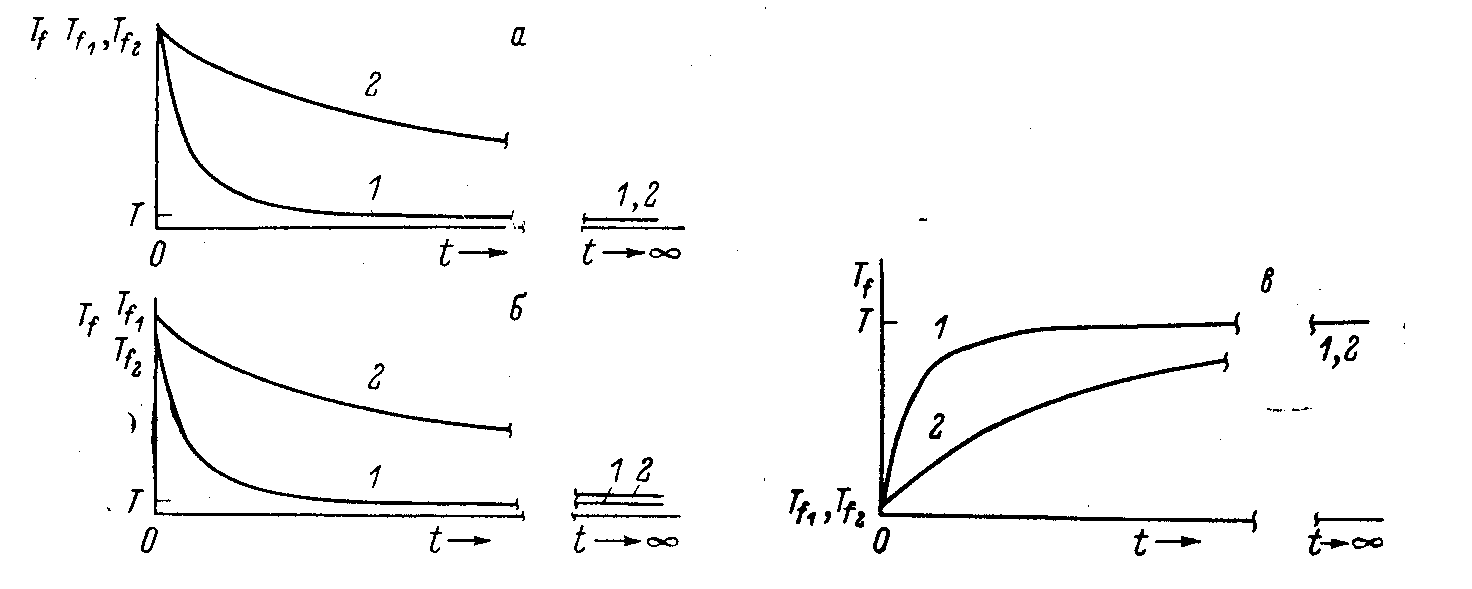- •Специальные разделы оптического материаловедения
- •Термодинамика фазовых равновесий
- •1.1 Общие сведения о термодинамике
- •1 Предмет термодинамики1
- •1.1.2 Термодинамическая система, виды систем
- •Изолированные системы – те, которые не имеют возможности обмениваться веществом и энергией с окружением и имеющие постоянный объем.
- •1.1.3 Параметры состояния, параметры процессов
- •1.1.4 Функции состояния
- •1.1.5 Виды процессов
- •1.1.6 Внутренняя энергия, теплота и работа
- •1.1.7 Максимальная работа при изобарических, изотермических, адиабатических и изохорных процессах
- •1.2 Законы термодинамики
- •1.2.2 II закон термодинамики и энтропия как термодинамическая функция
- •1.2.3 Энтропия и термодинамическая вероятность. III закон термодинамики
- •Следствия Законов
- •1.2.5 Термодинамические функции, важные для материаловедения.
- •1.2.6 Применение термодинамических понятий в других областях науки
- •1.3 Производные термодинамических потенциалов и фазовые переходы
- •1.3.1 Первые производные термодинамических потенциалов, их физический
- •1.3.2 Вторые производные термодинамических потенциалов (соотношения
- •1.3.3 Фазовые переходы I и II рода.
- •1.3.4 Фазовые переходы I рода. Барическая зависимость фазовых переходов I рода:
- •1.4 Теория фазовых равновесий
- •1.4.1 Понятия «фазовые равновесия», «компонент», «диаграмма состояний»,
- •1.4.2 Понятие химического потенциала. Условия равновесия фаз. Правило фаз
- •1.4.3 Диаграмма состояний однокомпонентной системы
- •1.4.5 Эвтектики (двухкомпонентные системы). Линии ликвидуса и солидуса.
- •1.4.6 Твердые растворы (двухкомпонентные системы). Значение твердых
- •1.4.7 Ограниченные твердые растворы
- •1.4.8 Упорядочение твердых растворов
- •1.4.9 Полная несмешиваемость в жидком и в твердом состояниях
- •1.4.10 Системы с расслаиванием в жидком состоянии. Стабильное и
- •1.4.11 Системы с образованием химических соединений (двухкомпонентные
- •1.4.12 Системы с образованием химических соединений (двухкомпонентные
- •1.4.13 Трёхкомпонентные системы (принципы изображения,
- •1.4.14 Комбинация элементов диаграмм состояний. Физико-химический анализ.
- •2. Фазовые переходы и кинетическая теория стеклования
- •2.1 Стеклование
- •2.1.1 Принципиальная особенность фазовых переходов I и II рода в общей
- •2.1.2 Природа взаимодействия в конденсированных системах (общие
- •Ионное взаимодействие
- •Взаимодействие в металлах
- •Ковалентное взаимодействие
- •Водородные связи
- •Взаимодействие Ван-дер-Ваальса
- •Энергия химических связей
- •2.1.3 Основные особенности строения жидкостей и принцип их обобщенного
- •2.1.4 Общие сведения о релаксационных процессах как о процессах перехода от
- •2.1.5 Равновесные и мгновенные свойства жидкостей
- •2.1.6 Переохлажденные жидкости как частный случай метастабильного
- •2.1.7 Проявление стеклования на свойствах жидкостей
- •2.1.8 Определение стеклообразного состояния как лабильного (абсолютно
- •2.1.9 Математическое описание стеклования в кинетической теории. Твердо- и
- •2.1.10 Время релаксации структуры и его зависимость от температуры.
- •2.1.11 Соотношение температур стеклования и плавления (правило «2/3»
- •2.2 Кристаллизация расплавов стекол
- •2.2.1 Термодинамические особенности метастабильной жидкости
- •2.2.2 Работа образования зародыша кристаллизации20
- •2.2.3 Кривые Таммана а) скорость зарождения и кривая зарождения.
- •Б) скорость роста и кривая роста.
- •2.2.4 Методы изучения кристаллизационной способности и её
- •А) политермический метод и диаграммы кристаллизационной способности
- •Б) фазовый состав и морфология кристаллов.
- •В) дифференциальный термический анализ.
- •Г) скорость кристаллизации
- •2.2.5 Типы кристаллизации
- •2.2.6 Катализированная кристаллизация; ситаллы
- •2.2.7 Связь кристаллизационной способности с диаграммой состояния
- •3.Термодинамика стеклообразного состояния
- •3.1.1 Термодинамические переменные, используемые при математическом
- •3.1.2 Математическое описание избыточной свободной энергии лабильной
- •3.1.3 Математическое условие стеклования, налагаемое на изменения
- •3.1.4 Соотношение Пригожина-Дефея и его экспериментальная проверка
- •3.1.5 Термодинамический инвариант стеклообразного состояния
- •3.1.6 Следствия, вытекающие из соотношений термодинамики
- •5. Релаксационные процессы в стеклообразном состоянии. Ионная проводимость и ионный обмен
- •5.1.1 Зависимость температуры стеклования от скорости охлаждения
- •5.1.2 Процессы и законы релаксационных изменений свойств, структурная
- •5.1.3 Оценка времени достижения равновесного состояния в процессе отжига
- •5.1.4 Физическое старение стекла при комнатной температуре52
- •5.1.5 Релаксационные явления при переходе через температуру стеклования
- •5.1.6 «Кроссовер эффект»
- •5.1.7 Расчёт изменения свойств при отжиге стекол на основании
- •5.2 Природа ионной проводимости и диффузии в стеклах.
- •5.2.1 Структура стекла и основы механизма
- •5.2.2 Законы диффузии и соотношение Нернста – Эйнштейна
- •5.2.3 Основное статистическое уравнение проводимости. Энергия активации.
- •5.2.4 Общие корреляции, ряд подвижностей
- •5.2.5 Основные закономерности электропроводности, определяемые составом
- •5.2.6 Ионообменные процессы и проблемы современной оптической технологии
- •5.2.7 Ионообменные процессы с растворами. Стеклянный электрод.
- •6. Взаимосвязь между основными видами релаксационных процессов в стеклах
- •6.4.1 Соотношение Максвелла для проводимости диэлектриков
- •6.4.2 Соотношение Максвелла для проводимости диэлектриков как основа связи
- •6.4.3 Экспериментальная проверка возможности расчёта температуры «ионного» максимума внутреннего трения по данным проводимости
- •7. Основные принципы химической устойчивости стекол
- •7.1.1 Практическая значимость свойства и его физико-химическое
- •7.1.2 Методы испытания и классификация стекол по группам
- •Группы химической устойчивости бесцветного оптического стекла к действию кислоты и дистиллированной воды
- •Группы химической устойчивости бесцветного оптического стекла к действию влажной атмосферы
- •7.1.3 Влияние компонентов состава стекла на химическую устойчивость
- •7.1.4 Способы защиты оптических деталей от химического разрушения
- •8. Специфика некоторых структурных явлений в регистрирующих средах
- •8.1. Фотоструктурные изменения в халькогенидных стеклах, их существо и
- •8.2 Структурно-фазовые изменения в жидких кристаллах и физико-химическая
- •8.2.1 Общие представления о жидких кристаллах
- •8.2.2 Специфика изменения электрических и магнитных свойств при
5.1.6 «Кроссовер эффект»
|
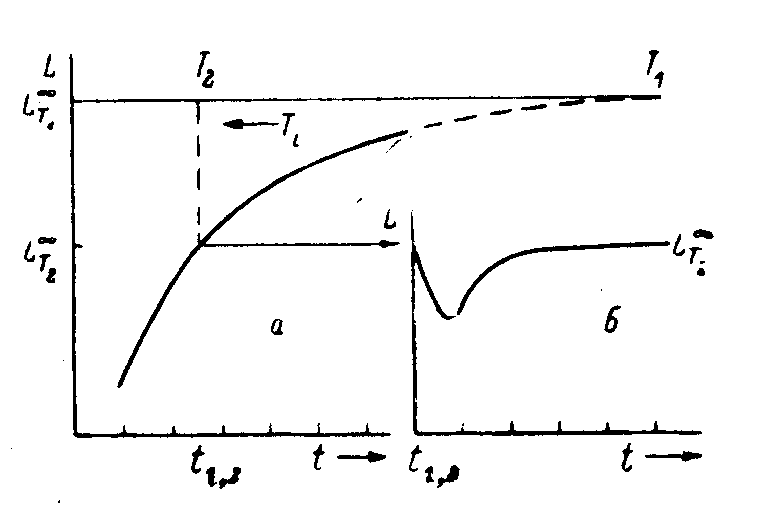
Рис. 63 «Кроссовер эффект». Пояснения в тексте. |
В середине 20 в. во всех странах очень подробно изучали кинетику отжига стекол по измерениям показателя преломления. В работах Флоринской, Ритланда, Спиннера и Наполитано, Маседо и Литовица, Купера и др. была отмечена чрезвычайно интересная особенность изменения показателя, если в процессе отжига стекла повысить температуру отжига и далее следить за изменением показателя во время этой новой изотермической обработки. Во многих случаях оказывается, что счала, после того как установили новую температуру, показатель изменяется в противоположную сторону, но затем приходит к постоянному значению. Интерпретация этого явления была самой разнообразной, но она сводилась к тому, что в релаксационном процессе участвуют области стекла, в которых релаксация протекает с сильно различающейся скоростью. Немиловым была предложена подробная интерпретация этого явления в терминах фиктивной температуры и структурных параметров54 [Немилов С.В. Физ. и хим. стекла т.12, №3, с. 293 (1986)]. Здесь излагается только сущность этой интерпретации.
В
верхней части рис. 63 приведена ось,
соответствующая значениям фиктивной
температуры; она возрастает справа
налево. Пусть закаленное стекло имело
очень высокую фиктивную температуру
(на рисунке она не обозначена, находится
слева). Свойство L в
процессе изотермического отжига при
температуре Т1 увеличивается (оно
может и уменьшаться, это значения не
имеет) и в пределе стремится к некоторому
пределу L![]() ,
соответствующему Т1. Если считать,
что структура стекла определяется
однозначно фиктивной температурой, то
кривая изменения свойства однозначно
соответствует шкале фиктивных температур.
В процессе приближения к равновесному
состоянию свойство стекла пробегает
последовательность значений, каждому
из них соответствует своё значение
фиктивной температуры (часть а
рисунка).
,
соответствующему Т1. Если считать,
что структура стекла определяется
однозначно фиктивной температурой, то
кривая изменения свойства однозначно
соответствует шкале фиктивных температур.
В процессе приближения к равновесному
состоянию свойство стекла пробегает
последовательность значений, каждому
из них соответствует своё значение
фиктивной температуры (часть а
рисунка).
Пусть при значении фиктивной температуры Т2, которая ниже первоначальной фиктивной температуры закаленного стекла, но выше чем Т1, мы перевели систему к этой температуре Т2 и продолжаем изотермический отжиг при этой температуре. Очень важно, что Т2 находится ниже той фиктивной температуры, которая была в стекле первоначально, но выше чем Т1.
Вместо
того чтобы свойство осталось неизменным
(если бы существовал единственный
параметр структуры), оно продолжает
изменяться, но уже в противоположном
направлении – оно уменьшается. Только
спустя некоторое время направление
процесса начинает соответствовать
ожидаемому и в пределе свойство стремится
к пределу L![]() , соответствующему новой фиктивной
температуре Т2 (часть б рисунка).
, соответствующему новой фиктивной
температуре Т2 (часть б рисунка).
В предыдущих разделах мы уже упоминали, что во всех стеклах необходимо предполагать существование не менее двух независимых параметров порядка; Мойниханом было показано, что такой случай должен неизбежно приводить к различной скорости их релаксационных изменений. Тогда скорость изменения свойства должна записываться через частные производные следующим образом:
![]()
![]() ∙
∙![]() +
+
![]() ∙
∙![]() .
.
Здесь каждая фиктивная температура соответствует релаксации отдельного параметра порядка. Из-за того, что параметры релаксируют с разной скоростью, с ходом времени расходятся и их фиктивные температуры (рис. 64). Поэтому в какой-то момент времени разница в фиктивных температурах, соответствующая этим параметрам, становится значительной. На рис. это кривые 1 и 2 которые могут совпасть при бесконечной продолжительности отжига, а могут и не совпасть. Часть а, соответствует случаю, когда температура стабилизации Т совпадает с температурой измерений, часть б соответствует случаю когда она выше температуры измерений. В обоих случаях температура стабилизации меньше и Тf1 и Тf2. Часть в рисунка соответствует случаю, когда Т совпадает с температурой измерений, но при начальном времени t она превышает и Тf1 и Тf2.
Из всего этого следует, что установив новую температуру Т2 и проводя измерения в процессе изотермического отжига мы можем попасть при выборе Т2 между двумя кривыми рисунка. Один параметр порядка уже отрелаксировал до этого при температуре Т1, а второй был еще далёк от завершения этого процесса.
Установив более высокую температуру Т2 чем была до этого температура Т1, мы заставляем один из параметров порядка (который более быстро изменялся) возвращаться к новому значению, в этом случае обратно, если говорить в терминах значений фиктивных температур. Это и приводит к уменьшению величины свойства (рис. 63). Но затем устанавливается нормальное направление изменения свойства, поскольку самый медленный параметр порядка продолжает стремиться к равновесному значению.
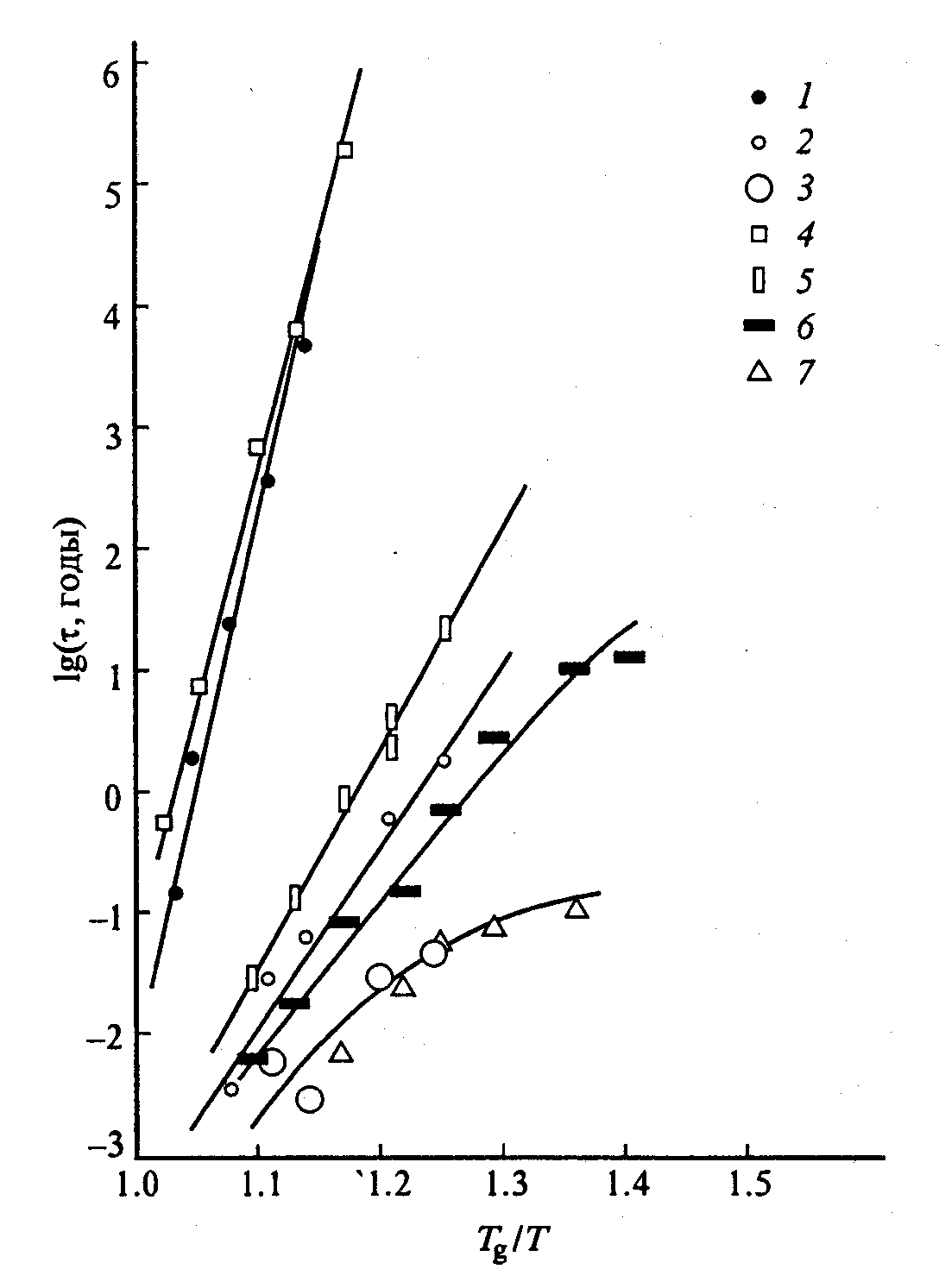
Существовавшие молекулярно-кинетические интерпретации этих изменений предполагали либо наличие в структуре областей разной химической природы (однако кроссовер наблюдался и в однокомпонентных стеклах, где такого быть не может), либо наличие в стекле разных времен релаксации, отличающихся не менее чем на порядок. В.А.Флоринская55 на основании очень тщательного изучения кинетики изменения показателя преломления оптических стекол намного ниже нормальной температуры отжига (1013 П) пришла к выводу, что существует несколько каналов релаксационного процесса, в разных областях температур проявляются лишь те, у которых более или мене соизмеримы времена релаксации и время наблюдений (рис. 65). Так это или не так, факты свидетельствуют о множественности параметров порядка, которые пока интерпретировать детально невозможно.
|
Рис. 64. К интерпретации возникновения «кроссовер» эффекта |
|
Рис. 65. Зависимости от приведенной температуры характеристических времен релаксационных каналов изменения показателя преломления при изотермическом отжиге стекол Ф1 и БК10, по В.А.Флоринской.
4 – БК10, канал α; 5 – канал β1; 6 –канал β2; 7 – канал β3.
|
Примечательно, что наиболее «естественным» для объяснения «кроссовер» эффекта явилась гипотеза о множественности параметров порядка, которой соответствует набор отличающихся каналов релаксации.
Описанные здесь эффекты не являются единственными, они рассмотрены здесь только как введение в сложный мир необратимых релаксационных процессов в стекле.