79. Дисперсія та середньоквадратичне відхилення як міра ризику. Наведіть приклад

Дисперсією (варіацією) V(X) випадкової величини Х є зважена щодо ймовірності величина квадратів відхилення випадкової величини Х від її математичного сподівання М(Х). Дисперсія характеризує міру розсіяння випадкової величини Х навколо М(Х) і обчислюється за формулою:

V(X) = M(X – M(X))2 = M(X2) – (M(X))2.

Для дискретної випадкової величини

Середньоквадратичним (стандартним) відхиленням випадкової величини Х називається величина

Підхід до оцінки ризику, що спирається на варіацію чи середньоквадратичне відхилення, вважається класичним. Причому чим більшими будуть ці величини, тим більшим буде ступінь ризику, пов’язаного з певною стратегією, тобто величина ризику

W = V(X) або W =  (X).

Слід зазначити, що такий підхід до оцінки ступеня ризику використовується, коли Х = Х .

Приклад Розглядаються два проекти А і В щодо інвестування. Відомі оцінки прогнозованих значень доходу від кожного з цих проектів та відповідні значення ймовірностей. Потрібно оцінити міру ризику кожного з цих проектів і обрати один з них (той, що забезпечує меншу величину ризику) для інвестування.

80. Семіваріація та семіквадратичне відхилення як міра ризику. Наведіть приклад

Якщо випадкова величина Х = {x1; …; xn} відображає прибутки (Х = Х+) і значення хi < M(X) (оцінка прибутку хі є реалізацією випадкової величини Х і є меншою від сподіваної величини прибутку), то це є ознакою несприятливої ситуації. В той же час додатне відхилення вказує на те, що реалізація випадкової величини (прибутку) є більшою, ніж сподівана величина, і це для менеджера (інвестора) є, очевидно, кращою, тобто сприятливою ситуацією.

в якості міри ризику використовується семіваріація, яка обчислюється за формулою:

де j — індикатор несприятливих відхилень, який визначають за формулою:

Якщо ж, наприклад, Х = {x1; …; xn} відображає можливі варіанти збитків (Х = Х –, тобто має негативний інгредієнт), то

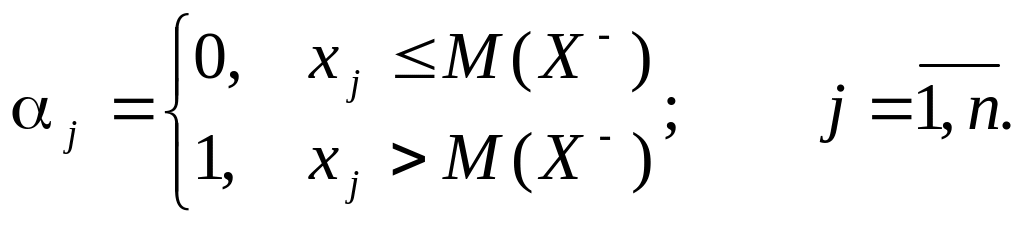
Для неперервної випадкової величини Х відповідно:

З практичної точки зору зручніше (беручи до уваги вимірність величин) застосовувати семіквадратичне відхилення.

Згідно із сказаним вище чим більшою буде величина SV(X) (чи SSV(X)), тим більшим буде ступінь ризику,

Приклад Результати спостережень за нормами прибутку портфелів цінних паперів А і В протягом минулих п’яти періодів наведено в табл.



Інвестор має можливість придбати лише один з цих портфелів. Потрібно оцінити міру ризику кожного з портфелів і придбати той, що забезпечує меншу величину ризику (для інвестування).

82. Поняття премії за ризик. Наведіть графічний приклад

За своїм фізичним змістом премія за ризик (надбавка за ризик) (Х) — це сума (в одиницях виміру критерію х), якою суб’єкт керування (особа, що приймає рішення) згоден знехтувати (уступити її) з середнього виграшу (тобто ця сума менша, ніж математичне сподівання виграшу), щоб уникнути ризику, пов’язаного з лотереєю.

Для зростаючих функцій корисності величину премії за ризик (Х) в лотереї L покладають рівною різниці між сподіваним виграшем та детермінованим еквівалентом

Нехай U(x) = а – be^–cx, де а > 0, b > 0, c > 0, x ≥ 0 (рис.4.1). Припустимо, що особа, яка приймає рішення, має справу з лотереєю L(x1, p; x2, q), p + q = 1. Відшукати сподіваний виграш та детермінований еквівалент.

81. Поняття корисності за Нейманом. Наведіть основні характеристики гри в лотерею, сподіваної корисності, страхової суми

Для визначення корисності розглядається вибір особи в умовах ризику, який формалізується за допомогою поняття лотереї.

Для цього необхідно з множини Х пред’явлених експертам значень певного економічного показника (об’єкта) виділити два значення х* та х* таких, що х ≥ х* та х ≤ х* для всіх х  Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показ­ника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне, в певному сенсі, значення показника (разом з «нулем» вони визначають масштаб даної шкали). Власне, так побудована функція корисності Дж. ф. Неймана і О.Моргенштерна. Експерту пропонують порівняти між собою дві альтернативи:

1) значення показника х;

2) лотерею: одержати х* з імовірністю 1 – р чи х* з імовірністю р. Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L(х*, p, x*) не стануть еквівалентними, тобто x  L(х*, p, х*).

Максимальному й мінімальному значенням х* та х* приписують довільні числові значення U*= U(х*) та U* = U(x*), але так, щоб U* > U*.

Під лотереєю L(x*, p(x), x*) розуміють ситуацію, у якій особа може отримати х* з імовірністю р(х) або х* з імовірністю 1 – р(х). (Часто використовують запис: L(x*, p(x); x*, q(x)), де q(х) = 1 – р(х)).

За Нейманом корисність варіанта х визначається ймовірністю U(х) = р(х), при якій особі байдуже, що обирати: х — гарантовано, чи лотерею L(х*, р(х), х*), де х*, х* — вектори, більш та менш пріоритетні порівняно з х.

Наприклад, у якості функції корисності можна брати функцію

бо для всіх x  [x*, x*] значення q(х)  [0; 1]. Оскільки при зростанні х від х* до х* значення q(х) будуть збільшуватися, то вибрана таким чином функція корисності буде зростаючою.

У якості функції корисності (згідно з Нейманом) можна використати функції розподілу ймовірностей:

U(x) = F(x) = P(X < x).

Hаприклад:

Сподівана корисність

Нехай L — лотерея, що приводить до виграшів (подій) x1, х2, ...., хn з відповідними ймовірностями p1, p2, ..., pn. Позначимо сподіваний виграш (математичне сподівання виграшу) через :

Справедлива основна формула теорії сподіваної корисності:

тобто корисність ансамблю результатів збігається з математичним сподіванням корисності результатів.

Поняття детермінованого еквівалента лотереї L є одним з основних при розгляді різних характеристик ризику та їхнього взаємозв’язку з функціями корисності.

Детермінований еквівалент лотереї L — це гарантована сума , отримання якої еквівалентне участі в лотереї, тобто   L. Отже, визначається з рівняння:

U( ) = M(U(Х)), або = U – 1(M(U(Х))),

де U – 1 () — функція, обернена до функції U(x).

Сподіваний виграш та детермінований еквівалент, що їх визначено вище, стосуються лотереї із скінченним числом можливих виграшів. Якщо можливі виграші описуються щільністю розподілу f(x), то сподіваний виграш у цій лотереї дорівнює:

а детермінований еквівалент можна знайти із співвідношень:

.

Страховою сумою (СС) називають величину детермінованого еквівалента, взяту з протилежним знаком:

CC(Х) = – .

Якщо особа, яка приймає рішення, стикається з несприятливою для неї лотереєю (тобто лотереєю, яка менш пріоритетна, ніж стан, у якому вона перебуває), то природно запитати, скільки б вона заплатила (в одиницях виміру критерію х) за те, щоб не брати участь у цій лотереї (уникнути її). Для визначення розмірів цього платежу вводиться до розгляду величина, яку називають премією за ризик.