47. Характерстики та статистичні властивості емпіричних параметрів оцінок β0*, β1*.

На основі центральної граничної теореми теорії ймовірностей можемо стверджувати, що випадкові величини β0*β1* й емпірична функція матимуть нормальний закон розподілу ймовір­ностей. Тоді, здійснюючи нормування цих величин, отримаємо:

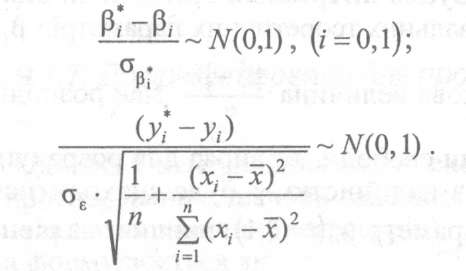
Оскільки тобто до складу е, входить випад­кова величина β*0 + β*1хi, що має нормальний закон розподілу, то на основі теорем теорії ймовірностей про побудову законів розподі­лу можна стверджувати, що ∑ei²буде розподілена за законом χ²

Тоді тобто

мають розподіл χ²із к = n - 2 ступенями свободи. А випадкові величини

тобто мають розподіл % із к = п - 2. Одержуємо, що

мають розподіл Стьюдента (t-розподіл) із к = n-2 ступенями свободи.

46. Параметри моделі парної лінійної регресії, їх сутність та оцінювання. Умови застосування мнк.

У загальному випадку парна лінійна регресія є лінійною функцією між залежною змінною Y і однією пояснюючою змінною X: Y=a0+a1X

Співвідношення називається теоретичною лінійною регресійною моделлю; a0 і a1 - теоретичні параметри (теоретичні коефіцієнти) регресії.

Зазначимо, що принциповою в цьому разі є лінійність за параметрами a0 і a1 рівняння.

Щоб визначити значення теоретичних коефіцієнтів регресії, необхідно знати й використовувати всі значення змінних X і Y генеральної сукупності, що практично неможливо. Тому за вибіркою обмеженого обсягу будують так зване емпіричне рівняння регресії, у якому коефіцієнтами є оцінки теоретичних коефіцієнтів регресії:

a0 і a1 - оцінки невідомих параметрів a0 і a1.

Для відображення того факту що кожне індивідуальне значення Уі відхиляється від відповідного умовного математичного сподівання, у модель уводять випадковий доданок и:

Отже, індивідуальні значення Уі подають у вигляді суми двох компонент - систематичної (a0+a1х{) і випадкової.

Щоб застосувати 1МНК для оцінки параметрів моделі, необхідне вико-нання таких умов:

1) математичне сподівання залишків дорівнює нулю, тобто M(u)=0.

2) значення u_i вектора залишків u незалежні між собою і мають постійну дисперсію, тобто

де Е — одинична матриця;

3) незалежні змінні моделі не пов’язані із залишками:

(4.4)

4) незалежні змінні моделі утворюють лінійно незалежну систему векторів, або, іншими словами, незалежні змінні не повинні бути мультиколінеарними, тобто :

(4.5)

де X_k — k-й вектор матриці пояснювальних змінних; X_j — j-й вектор цієї матриці пояснювальних змінних X, .

48. Суть і обчислення коваріаційної матриці оцінок параметрів моделі

У класичній регресійній моделі Y = XA + u вектор і залежний від нього вектор є випадковими змінними. До оператора оцінювання входить вектор Y ( ), а отже, оператор також можна вважати випадковою функцією оцінювання параметрів моделі.

Відомо, що для характеристики випадкових змінних , поряд з математичним сподіванням, застосовуються також дисперсія і коваріація (j  k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю

(4.16)

Оцінки коваріаційної матриці використовуються для знаходження стандартних помилок та обчислення довірчих інтервалів оцінок параметрів . Вони використовуються й при перевірці їх статистичної значущості. На головній діагоналі матриці містяться оцінки дисперсій j-ї оцінки параметрів, що ж до елементів (j  k), які роз­міщені поза головною діагоналлю, то вони є оцінками коваріації між і .

Отже,

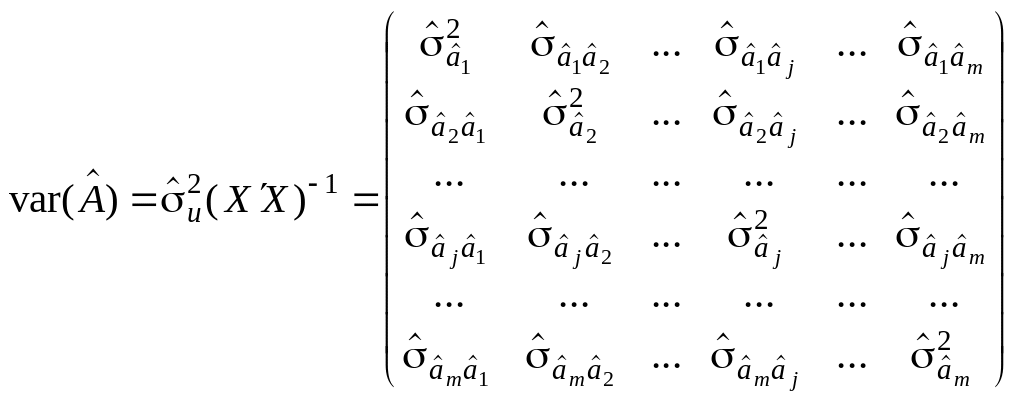, (4.17)

де — незміщена оцінка дисперсії залишків;

.

Оскільки вектор залишків , то добуток векторів можна записати так: .

Звідси маємо альтернативну форму запису дисперсії залишків:

Позначимо (j, k)-й елемент матриці символом , тоді j-й елемент по головній діагоналі матриці обчислюється за формулою: .

Коваріації , що містяться за межами головної діагоналі, відповідно такі:

.