39. Опишіть сутність теореми Куна-Таккера.

Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді: , , .(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)).

Теорема 8.1. (Теорема Куна—Таккера). Вектор Х^* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор , що при для всіх точка є сідловою точкою функції Лагранжа ,

і функція мети для всіх угнута, а функції — опуклі.

40. Опишіть сутність опуклого програмування

Нехай задано n-вимірний лінійний простір Rⁿ. Функція F(X), що задана на опуклій множині , називається опуклою, якщо для будь-яких двох точок X1 та X2 з множини X і будь-яких значень виконується співвідношення:

. (8.27)

Якщо нерівність строга і виконується для , то функція F(X) називається строго опуклою. Опукле програмування розглядає методи розв’язування задач нелінійного програмування, математичні моделі яких містять опуклі або угнуті функції. Загальний вигляд задачі опуклого програмування такий: , , ; , де , — угнуті функції.Аналогічний вигляд має задача для опуклих функцій. Позначимо: , тоді , і маємо: , ; , де , — опуклі функції. Оскільки ці задачі еквівалентні, то нижче розглянемо задачу . Множина допустимих планів задачі, що визначається системою , є опуклою.Як наслідок теорем 8.2 та 8.3 справджується таке твердження: точка локального максимуму (мінімуму) задачі опуклого програмування є одночасно її глобальним максимумом (мінімумом).Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа.

41. Постановка задачі квадратичного програмування та її математична модель.

До задач квадратичного програмування належать задачі, які мають лінійні обмеження, а функціонал являє собою суму лінійної і квадратичної функцій:

Квадратична функція n змінних називається квадратичною формою і може бути подана у вигляді:

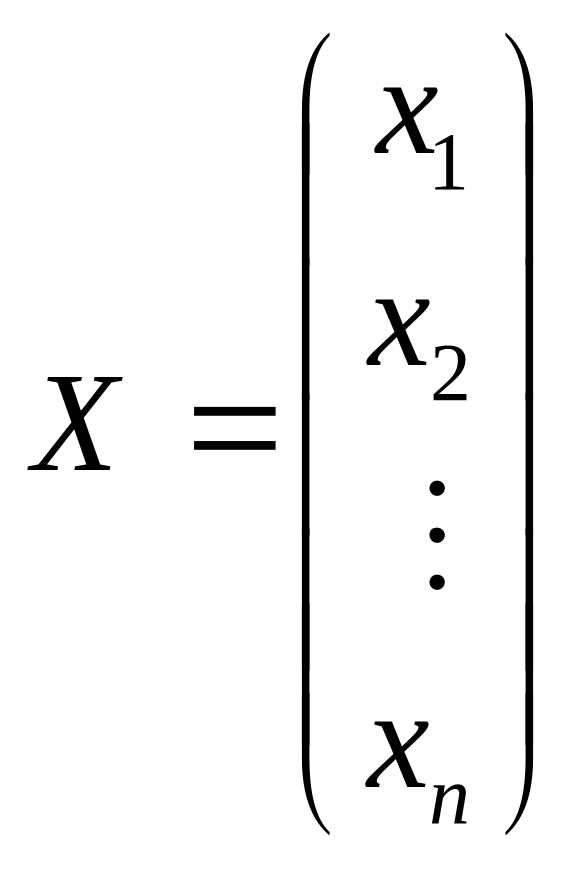
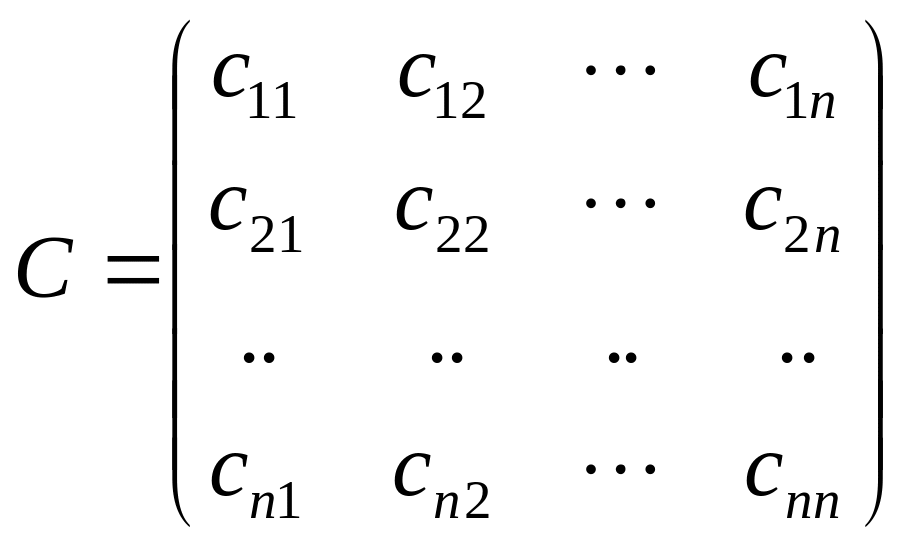
причому матриця С завжди симетрична, тобто для всіх .

Квадратична форма Z(X) називається від’ємно означеною, якщо для всіх Х, крім Х = 0, значення Z(X) < 0 (якщо Z(X) ≤ 0, то маємо від’ємно напівозначену квадратичну форму), у протилеж-ному разі Z(X) є додатно означеною (якщо Z(X) ≥ 0, то маємо додатно напівозначену квадратичну форму).

42. Градієнтні методи розв’язання задач нелінійного програмування та їх класифікація.

Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише певне наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються. В основі градієнтних методів лежить основна властивість градієнта диференційовної функції — визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.

1. Методи, при використанні яких досліджувані точки не виходять за межі області допустимих розв’язків задачі . Найбільш поширеним з таких методів являється метод Франка – Вулфа .

2. при використанні яких досліджуємі точки можуть як належити , так і не належити області допустимих розв’язків .Однак в результаті реалізації ітераціонного процесу находиться точка області допустимих розв’язків, оприділяюча прийнятне розв’язання. Із цих методів найбільш часто використовується метод штрафних функцій або метод Ерроу—Гурвіца .