
- •Статистика
- •Понятие статистического показателя. Атрибуты статистического показателя. Виды статистических показателей.
- •Понятие средней величины. Средняя арифметическая и ее свойства.
- •Количественная оценка тесноты связи по эмпирическим данным: эмпирический коэффициент детерминации, эмпирическое корреляционное отношение.
- •Количественная оценка тесноты связи по эмпирическим данным: коэффициент линейной парной корреляции.
- •Расчет параметров уравнения линейной множественной регрессии и их интерпретация.
- •Статистические методы прогнозирования вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •При косвенном методе величина рассчитывается опосредованно, через другие величины, связанные с искомой определенной зависимостью. Относительные величины измеряются только косвенным методом.
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Вопрос 11
- •Ч исло групп для удобства возьмем равным 3. Тогда величина интервала будет равна:
- •Вопрос 12
- •Пример: построим равнонаполненную группировку совокупности 20 студентов по признаку «посещаемость практических занятий» - х.
- •Вопрос 13
- •Сложные группировки (группировки по нескольким признакам) делятся на комбинационные и многомерные.
- •Комбинационная группировка студентов по признакам: оценка (y) и посещаемость практических занятий (X):
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Кумулятивные ряды распределения – ряды распределения, которые содержат один или оба следующих элемента:
- •Вопрос 17 Графические представления рядов распределения
- •Вопрос 18 Понятие средней величины. Средняя арифметическая и ее свойства.
- •Вопрос 19
- •Понятие ведущего показателя
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Вопрос 24 Показатели формы распределения. Ответ
- •Вопрос 25 Нормальное распределение и его свойства.
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31 Способы отбора. Ответ
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 36 Количественная оценка тесноты связи по эмпирическим данным: эмпирический коэффициент детерминации, эмпирическое корреляционное отношение. Ответ
- •Вопрос 37 Количественная оценка тесноты связи по эмпирическим данным: коэффициент линейной парной корреляции. Ответ
- •Вопрос 38
- •Вопрос 39
- •Вопрос 40
- •Вопрос 41
- •Вопрос 42
- •Вопрос 43
- •Вопрос 44 Расчет параметров уравнения линейной множественной регрессии и их интерпретация.
- •Вопрос 45
- •Вопрос 46
- •Вопрос 47
- •Вопрос 48
- •Вопрос 49
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Добыча нефти в Российской Федерации, млн.Тонн
- •Вопрос 53
- •Область допустимых значений у Кр и Тр от нуля до плюс бесконечности.
- •Используется для правильной оценки значения полученного темпа прироста. Аi показывает какое абсолютное значение скрывается за относительным показателем 1% прироста.
- •Вопрос 54
- •Вопрос 55
- •Вопрос 56
- •Вопрос 57
- •Вопрос 58
- •Вопрос 59 Статистические методы прогнозирования
Вопрос 40
Оценка качества уравнения регрессии.
ОТВЕТ
Под качеством уравнения регрессии понимается степень близости (соответствия) рассчитанных по данному уравнению значений признака-результата (Y’) к фактическим (наблюдаемым) значениям Y.
Для оценки качества полученного уравнения регрессии используется ряд показателей. Наиболее широкое применение из них получил теоретический коэффициент детерминации – R2yx. Теоретический коэффициент детерминации рассчитывается, как отношение объясненной уравнением дисперсии признака-результата - 2, к общей дисперсии признака-результата 2y :
 ,
,
где 2 – объясненная уравнением регрессии дисперсия Y;
2y - общая (полная) дисперсия Y.
В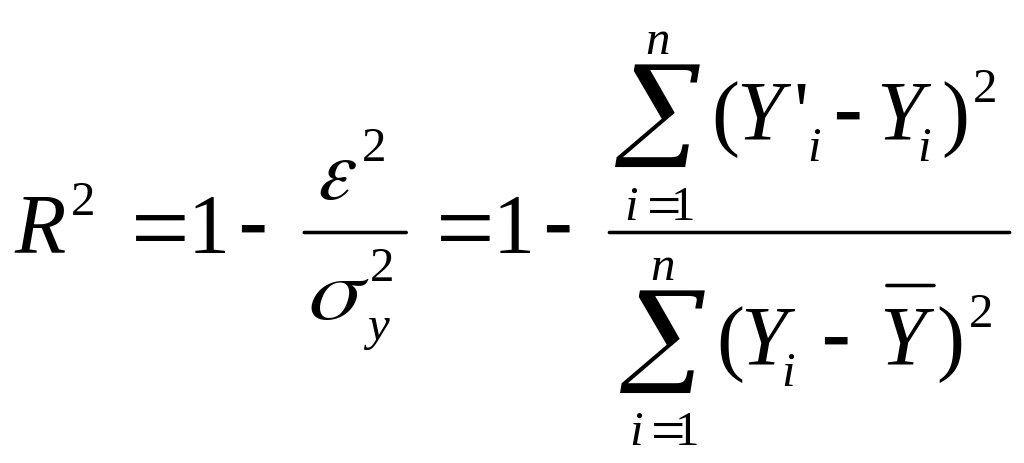 силу теоремы о сложении дисперсий общая
дисперсия результативного признака
равна сумме объясненной уравнением
регрессии (2)
и остаточной (необъясненной) (2)
дисперсий: 2y=2+2.
Поэтому коэффициент детерминации может
быть рассчитан через остаточную и общую
дисперсии:
силу теоремы о сложении дисперсий общая
дисперсия результативного признака
равна сумме объясненной уравнением
регрессии (2)
и остаточной (необъясненной) (2)
дисперсий: 2y=2+2.
Поэтому коэффициент детерминации может
быть рассчитан через остаточную и общую
дисперсии:
где 2- остаточная (необъясненная уравнением регрессии) дисперсия Y.
Данный показатель характеризует долю вариации (дисперсии) результативного признака Y, объясняемую уравнением связи (а, следовательно, и фактором Х), в общей вариации (дисперсии) Y. Коэффициент детерминации R2yx принимает значения от 0 до 1. Соответственно величина 1-R2yx характеризует долю дисперсии Y, вызванную влиянием прочих неучтенных в уравнении факторов и ошибками измерений.
При парной линейной регрессии R2yx=r2yx.
Вопрос 41
Задачи изучения множественной связи.
ОТВЕТ
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. В экономике (в отличие от естественных наук) невозможно контролировать поведение большинства экономических факторов. Влияние данных факторов нужно учитывать в модели. То есть нужно построить уравнение, описывающее множественную связь:
Y=f(X1, X2, ...,Xm, u),
где Y – признак-результат;
X1, X2, ...,Xm - признаки-факторы;
u – случайная составляющая.
Задачи анализа многофакторной зависимости:
сравнение степени влияния различных факторов на результат;
выделение прямого (непосредственного) влияния фактора на результат и косвенного (опосредованного) влияния фактора на результат (через другие факторы);
выявление существенности влияния данного фактора (или группы факторов) на результат на фоне других факторов (т.е. нельзя ли исключить из модели данный фактор без существенного ухудшения описания результирующей переменной).
Изобразим графически связи всех признаков для двухфакторной регрессии: Y=f(X1,X2,u) (рис.15).
Н еучтенные
в модели
ф
еучтенные
в модели
ф акторы
акторы
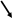
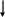
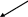





 Y
Y
 X1
X2
X1
X2
 - прямые связи
- прямые связи
п
 олные
связи
олные
связик
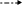 освенные
(опосредованные) связи
освенные
(опосредованные) связи
Рис. 15. Граф связей модели: Y=f(Х1, Х2).
Вопрос 42
Регрессия в стандартных масштабах.
ОТВЕТ
Уравнение регрессии в стандартном масштабе связывает стандартизованные значения признаков. То есть все значения исследуемых признаков переводятся в стандарты по формулам:
для
признаков -факторов
![]() ,
j=1;m,
,
j=1;m,
где Хji - значение переменной Хji в i-ом наблюдении;
для
признака – результата
![]() .
.
Таким
образом, начало отсчета каждой
стандартизованной переменной совмещается
с ее средним значением, а в качестве
единицы изменения принимается ее среднее
квдратическое отклонение. Благодаря
этому все переменные в стандартизованном
масштабе имеют одинаковые средние
арифметические значения равные 0 (![]() )
и одинаковые дисперсии равные 1
(tx2=ty2=1).
Кроме того, коэффициент парной линейной
корреляции между стандартизованными
переменными равен среднему из произведений
данных стандартизованных переменных:
)
и одинаковые дисперсии равные 1
(tx2=ty2=1).
Кроме того, коэффициент парной линейной
корреляции между стандартизованными
переменными равен среднему из произведений
данных стандартизованных переменных:
![]() ,
,
![]() .
.
Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
![]() ,
,
где j – параметры уравнения регрессии в стандартном масштабе.
-коэффциенты могут быть оценены с помощью обычного МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=1+rx1x22+…+ rx1xmm
rx2y= rx2x11+2+…+ rx2xmm
…
rxmy= rxmx11+rxmx22+…+m
Найденные из данной системы –коэффициенты показывают на какую часть своего среднего квадратического отклонения изменится признак-результат Y с изменением соответствующего фактора Хj на величину своего среднего квадратического отклонения (хj) при неизменном влиянии прочих факторов (входящих в уравнение).
Кроме
того, коэффициент j
может интерпретироваться как показатель
прямого (непосредственного) влияния
j-ого
фактора (Xj)
на результат (Y).
Во множественной регрессии j-ый
фактор оказывает не только прямое, но
и косвенное (опосредованное) влияние
на результат (т.е. влияние через другие
факторы модели). Косвенное влияние
измеряется величиной:
![]() ,
где m-
число факторов в модели. Полное влияиние
j-ого
фактора на результат равное сумме
прямого и косвенного влияний измеряет
коэффициент линейной парной корреляции
данного фактора и результата – rxj,y.
Таким образом: rxj,y=j+
.
,
где m-
число факторов в модели. Полное влияиние
j-ого
фактора на результат равное сумме
прямого и косвенного влияний измеряет
коэффициент линейной парной корреляции
данного фактора и результата – rxj,y.
Таким образом: rxj,y=j+
.
