Вопрос 25 Нормальное распределение и его свойства.

ОТВЕТ

Нормальное распределение может быть представлено графически в виде симметричной куполообразной кривой (рис. 6.). Куполообразная форма кривой показывает, что большинство значений концентрируется вокруг центра измерения. Уравнение нормальной кривой: ,

где Y_i- ордината кривой нормального распределения; =3,1415 и е=2,7182 – математические константы, a – математическое ожидание Х (для статистической совокупности a= ), - среднее квадратическое отклонение.

Рис. 6. Нормальное распределение.

Основные особенности кривой нормального распределения:

1. Кривая симметрична относительно максимальной ординаты, которая соответствует значению х=Мо=Ме= , ее величина равна .

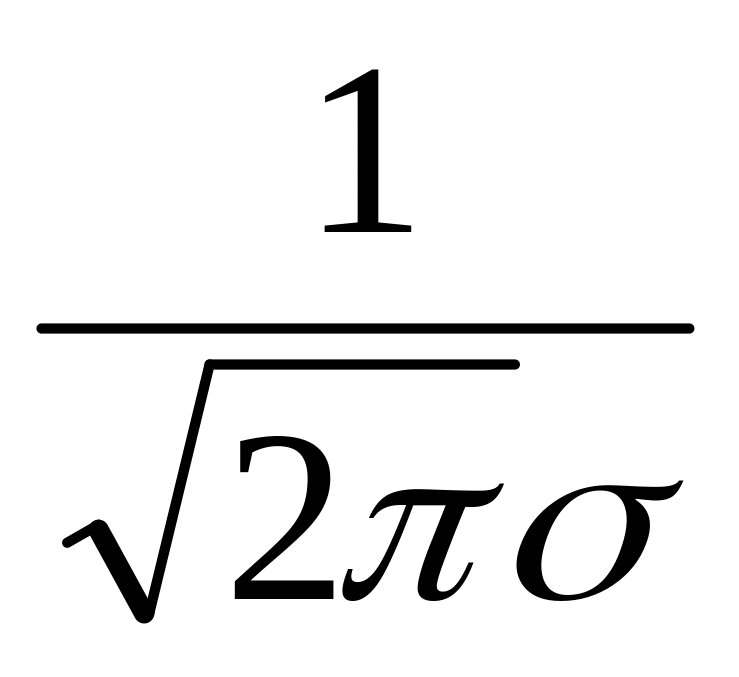2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от Х, тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной Х от равновероятны.

3. Кривая имеет 2 точки перегиба, находящиеся на расстоянии  от .

4. При =const с увеличением  кривая становится более пологой. При =const с изменением кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.

5. В промежутке  находится 68,3% всех значений признака. В промежутке 2 находится 95,4% всех значений признака. В промежутке 3 находится 99,7% всех значений признака.

6. Параметры нормального распределения: Мо=Ме= , Аs=0, Ех=0.

7. Нормальное распределение с параметрами а=0 и =1 называется стандартным нормальным распределением.

Вопрос 26

Сравнение эмпирического и теоретического распределений вариационных рядов.

ОТВЕТ

В вариационных рядах существует определенная связь между изменениями частот и значений варьирующего признака. Такого рода изменения называются закономерностями распределения. Для дискретного признака имеет место зависимость частостей (играющих роль вероятностей) от значения признака Х. Для непрерывного признака – зависимость между плотностями распределения частот и значениями признака.

Теоретическое распределение – хорошо известное и изученное в теории распределение. Оно описывается конкретной функцией (формулой). Параметры данной функции вычисляются по статистическим характеристикам совокупности.

Наиболее широкое практическое использование получили следующие виды распределений:

Для дискретного признака:

• распределение Пуассона;

для непрерывного признака:

• нормальное распределение;

• экспоненциальное распределение

Эмпирические (фактические) закономерности отражают ряды распределения, а графически оно представляется с помощью полигона и гистограммы распределения. Фактическое распределение отличается от теоретического в силу влияния случайных факторов. Их влияние сглаживается с увеличением объема исследуемой совокупности.

Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что признак Х распределен по данному теоретическому закону. Объективную оценку близости эмпирических частот к теоретическим можно получить с помощью определенных критериев согласия. Существует множество таких критериев.

Наиболее широкое распространение получил критерий согласия «хи-квадрат» (или критерий Пирсона). Данный критерий применяется для сгруппированных данных. Он представляет собой случайную величину, имеющую распределение близкое к распределению «хи-квадрат», которую определяют по формуле:

²(X)=_j=1;m(N_j- N'_j)²/N’_j ,

где m-число групп;

N_j – эмпирическая частота в j-ой группе;

N'_j – теоретическая частота в j-ой группе.

Если расхождение между сравниваемыми эмпирическими и теоретическими частотами распределения окажется слишком большим, т.е. ²(X) будет принимать большие численные значения, то считают, что эмпирическое распределение сильно отличается от теоретического. А если расхождение окажется небольшим, то предполагают, что эмпирическое распределение близко к теоретическому.

Оценку существенности величины ²(X) можно получить, сравнив вычисленное по наблюдаемым данным значение критерия с табличным (критическим) значением - (²_кр). Если ²(X)<²_кр, то считают, что отличие фактического распределения от теоретического несущественно; а если ²(X) >²_кр, то отличие существенно.

²_кр определяют по статистическим таблицам значений ²–критерия Пирсона в зависимости от уровня значимости  (вероятности того, что в наших выводах будет допущена ошибка) и параметра k, который равен: k=m-h-1, где h- число оцененных параметров теоретического распределения по наблюдаемым значениям признака.

Если проверяется гипотеза для дискретного ряда распределения, то порядок расчета ²(Х) следующий:

1. строится эмпирический ряд распределения и находятся эмпирические частоты N_j. При этом может оказаться, что для некоторых групп N_j <5 (обычно в начале или конце ряда). Такие группы следует объединить с соседними, чтобы условие N_j ≥5 выполнялось для всех групп.

2. рассчитываются теоретические вероятности p_j, для объединенных групп соответствующие вероятности суммируются. Если параметры теоретического распределения неизвестны, то их оценивают по наблюдаемым значениям признака (например, методом максимума правдоподобия).

3. вычисляются ожидаемые частоты: N’_j =N· p_j , где N – объем совокупности;

4. вычисляется значение критерия «хи-квадрат» по формуле одноименной формуле.

Если исследуемая переменная непрерывна, то порядок расчета остается прежним. При этом эмпирический ряд распределения строится как интервальный. Теоретические вероятности p_j рассчитываются через интегральную функцию теоретического распределения - F(Х), как:

p_j= F(Х^в_j) - F(Х^н_j),

где Х^в_j и Х^н_j - соответственно верхняя и нижняя границы j–го интервала.

После этого может быть применена описанная выше методика расчета.