Вопрос 20

Усреднение относительных величин.

ВОПРОС

Если требуется найти среднее значение относительного показателя x, представляющего собой отношение абсолютных показателей (y и z): x=y/z, то используют формулу:

.

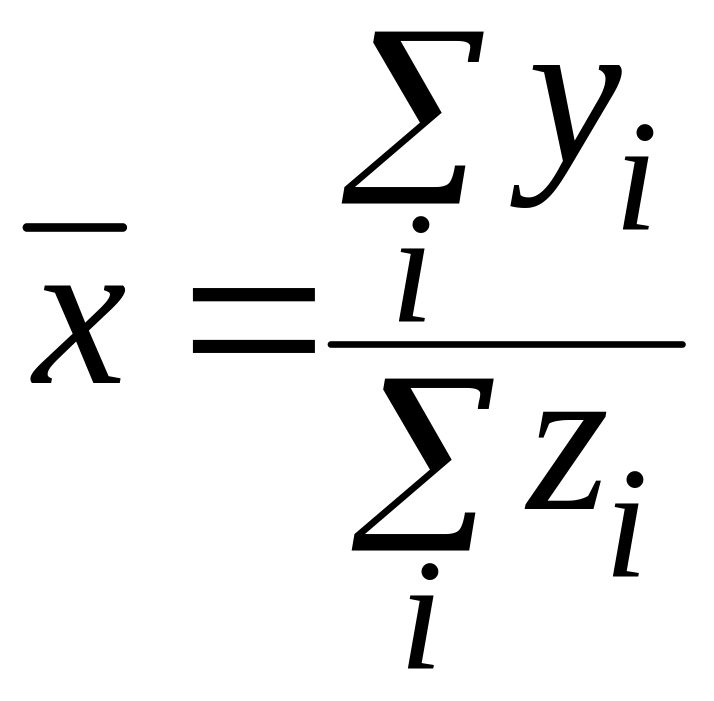В зависимости от имеющихся данных формула расчета среднего значения x может быть сведена к формуле среднего арифметического взвешенного либо среднего гармонического взвешенного.

Когда имеются данные об индивидуальных значениях относительного показателя x и индивидуальных значениях абсолютного показателя знаменателя (z) в совокупности, то значения показателя y могут быть вычислены как: y=z·x и формула расчета будет иметь вид:

.

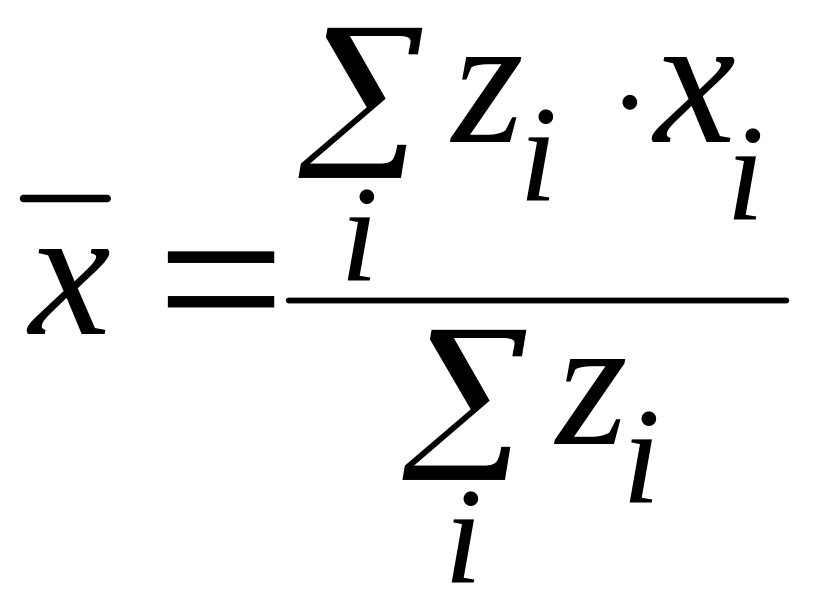Это формула среднего арифметического взвешенного, где x_i усредняемые значения показателя, z_i - веса усреднения.

Когда имеются данные об индивидуальных значениях относительного показателя x и абсолютного показателя числителя (y), то значения показателя z могут быть вычислены как: z=y/x и формула расчета будет иметь вид:

.

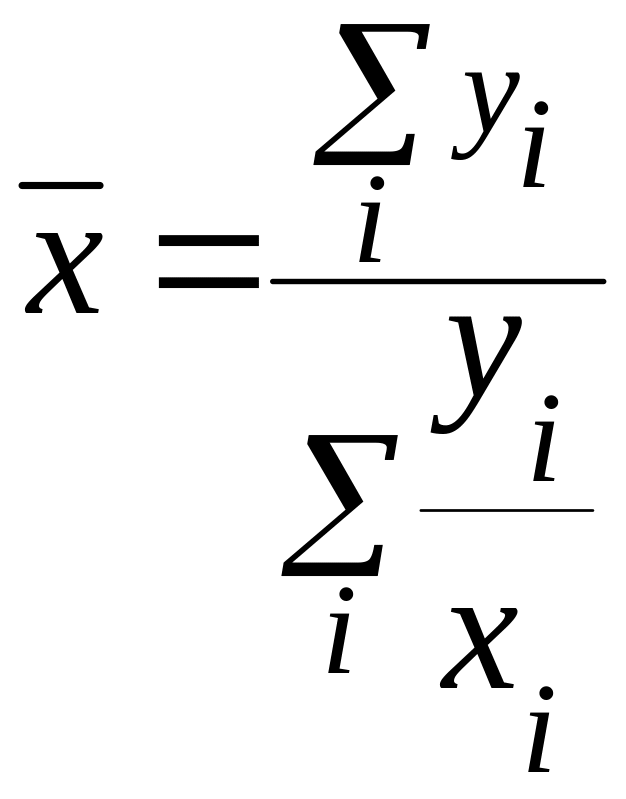Это формула среднего гармонического взвешенного, где x_i усредняемые значения показателя, y_i - веса усреднения.

Рассмотрим пример. На основе имеющихся данных (табл.) требуется определить среднюю цену:

Таблица

N магазина	Цена картофеля, руб/кг (x)	Выручка от реализации продукции, тыс.руб. (y)
1-ый	6	24
2-ой	5	15
3-ий	4	20
Итого	-	59

Расчет средней цены выражается соотношением:

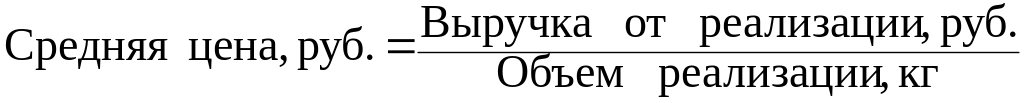
Выручка от реализации известна, а объем реализации нет. Однако мы можем рассчитать объем реализации как частное от деления выручки на цену. Тогда средняя цена 1 кг картофеля по трем магазинам может быть исчислена по формуле средней гармонической взвешенной:

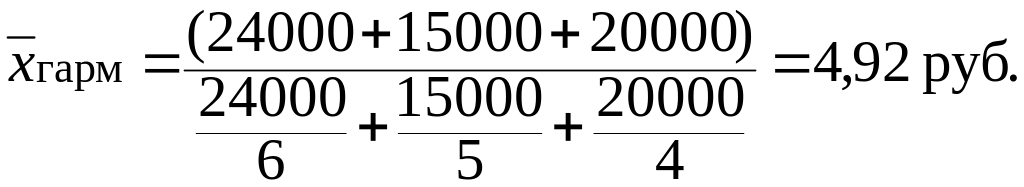
Этот же результат получится и по формуле средней арифметической взвешенной, если в качестве весов принять объем реализации (кг), который необходимо предварительно рассчитать:

Исчисление средней гармонической взвешенной избавляет от предварительного расчета весов, поскольку эта операция заложена в саму формулу.

Вопрос 21

Структурные характеристики распределения: квантили распределения и мода.

ОТВЕТ

К структурным характеристикам ряда распределения относят квантили распределения (медиану, квартили, децили и др.) и моду.

Квантили распределения представляют собой обобщающие показатели, характеризующие структуру распределения признака в совокупности.

Квантиль – это значения признака Х, занимающее определенное место в упорядоченной по данному признаку совокупности.

Виды квантилей:

1. медиана – Ме значение признака, приходящееся на середину упорядоченной совокупности,

2. квартили Q_1/4, Q_2/4=Ме, Q_3/4 – значения признака, делящие упорядоченную совокупность на 4 равные части,

3. децили Q_0,1,Q_0,2,…,Q_0,9 – значения признака, делящие упорядоченную совокупность на 10 равных частей,

4. процентили Q_0,01,Q_0,02,…,Q_0,99 - значения признака, делящие упорядоченную совокупность на 100 равных частей.

Рассмотрим пример. Определим медиану для признака Х «посещаемость практических занятий по статистике» в совокупности 20 студентов. Для этого упорядочим совокупность по Х:

N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

X 0 3 4 5 6 | 7 7 9 10 10 |10 12 12 14 15 | 15 16 16 16 16

Q_1/4 Q_2/4=Ме Q_3/4

В совокупности 20 единиц. Середина приходится на 10 и 11 элементы, значения признака у которых 6 и 7 соответственно. Медианой будет среднее из значений этих элементов Х₁₀=10, Х₁₁=11, т.е. Ме=(10+10)/2=10.

Первый квартиль отделяет первую четверть элементов совокупности (т.е. 5 элементов). Его значение будет равно среднему из значений признака у 5-ого и 6-ого элементов, т.е. Q_1/4=(6+7)/2=6,5.

Третий квартиль отделяет последнюю четверть элементов совокупности. Его значение будет равно среднему из значений признака у 15-го и 16-го элементов, т.е. Q_3/4=(15+15)/2=15.

Если данные сгруппированы, то значение квантиля определяется по накопленным частотам: номер группы (j), которая содержит i-ый квантиль, определяется как номер первой группы от начала ряда, в которой сумма накопленных частот равна или превышает N·i, где i- индекс квантиля.

Если ряд интервальный, то значение квантиля уточняется по формуле:

(*),

где X_Qi- нижняя граница интервала, в котором находится i-ый квантиль;

F_(-1) – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится i-ый квантиль;

N_Qi – частота интервала, в котором находится i-ый квантиль.

Рассмотрим пример: определим медиану распределения признака «посещаемость практических занятий по статистике» в совокупности студентов по сгруппированным данным (равноинтервальная группировка):

Таблица 1

Посещаемость – (Xн i; X вi)	Количество студентов	Накопленная частота (количество студентов нарастающим итогом)
[0 ; 5,3]	4	4
(5,3 ; 10,6]	7	11
(10,6; 16]	9	20
Итого	N=20	Х

Определим номер группы, содержащей Ме. Это будет 2-ая группа, т.к. именно в нее попадают серединные элементы совокупности (Накопленная частота F₂=11, что больше N·0,5=10).

Теперь уточним значение Ме по формуле (*) :

Q_2/4=Me=5,3+5,3·(10-4)/7=9,84.

X_Q2/4=5,3; _Q2/4=5,3; F_(-1)=F₁=4; N_Q2/4=7.

Еще один способ определения квантилей - графический по кумуляте распределения (см. рис.1).

Н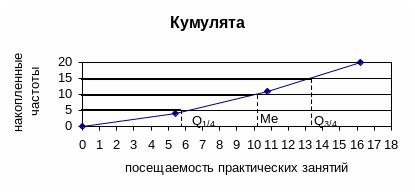 апример, для определения медианы высоту наибольшей ординаты кумуляты, которая соответствует общей численности совокупности (N) делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой. Для определения квартилей высоту наибольшей ординаты делят тремя точками на три равные части. Через эти точки проводят прямые параллельные оси абсцисс до пересечения с кумулятой. Абсциссы точек пересечения и будут искомыми значениями квартилей.

Рис. 1. Определение медианы и квартилей по кумуляте.

Наиболее распространенным видом квантилей является медиана. Медиана не требует знания всех индивидуальных значений признака. Она не чувствительна к крайним значениям признака, которые могут резко отличаться от основной массы его значений. Поэтому медиану используют как наиболее надежный показатель типичного значения признака в неоднородной совокупности (включающей резкие отклонения от ).

Медиана находит практическое применение также вследствие особого математического свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая: (Х_i-Ме)min.

Мода (Мо[х]) – наиболее часто встречающееся значение признака в совокупности.

Для дискретного ряда мода – это значение признака, которому соответствует наибольшая частота (частость) распределения. Для интервального ряда – это значение признака, которому соответствует наибольшая плотность распределения. Если ряд равноинтервальный, то значение моды можно определить по частотам (частостям): их соотношение будет таким же, что и плотностей распределения. Кроме того, значение моды в случае равноинтервального ряда можно уточнить по формуле:

Мо=Х_Мо+_Мо ·(N_Mo-N_Mo-1) / (N_Mo-N_Mo-1 +N_Mo-N_Mo+1),

где N_Mо, N_Mо-1, N_Mо+1 – частоты, соответственно, модального, предшествующего и последующего интервалов.

Рассмотрим пример: определим моду для распределения признака «посещаемость практических занятий по статистике» в совокупности студентов, используя данные равноинтервальной группировки (табл.1). Модальный интервал будет [10,6 –16], т.к. в этом интервале наибольшая частота (N_M0=9). Приближенное значение Мо определим по формуле: Мо=10,6+5,3(9-7)/(9-7+9-0)=11,56.

М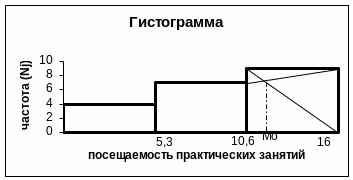 ода равноинтервального ряда графически определяется по гистограмме распределения (см. рис.2). Для этого правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Рис.2. Определение моды по гистограмме

Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды. Если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариант больше двух, то ряд – полимодальный.

Мода также как и медиана не требует знания всех индивидуальных значений признака и поэтому может быть использована в качестве наиболее типичного значения признака в неоднородной совокупности.