1.1.4. Задачі теорії потоків і лінійного програмування

Для подальшого нам знадобляться знання про властивості прямої і двоїстої задачі лінійного програмування. Сформулюємо ці властивості в іншій формі, ніж вони звичайно розглядаються в дослідженні операцій [4, 5]. Наведемо ці властивості без доведення. Пряма задача формулюється таким чином. Потрібно визначити значення змінних , які задовольняють співвідношенням

(1.24)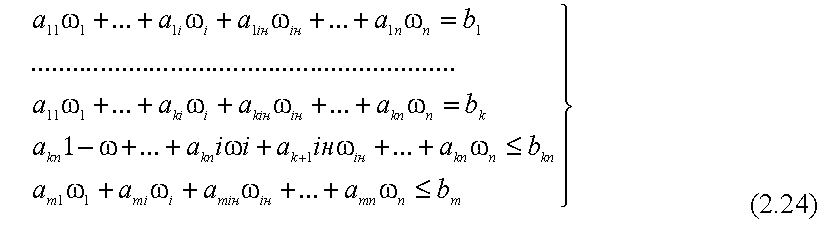

і падають максимуму лінійній формі

(1.25)

Для подальшого важливо, що величина мають любі знаки, а величини (ці змінні відповідають нерівностям двоїстої задачі).

Цій прямій задачі ставиться у відповідність двоїста задача. При цьому кожному з обмежень (1.24) ставляться у відповідність двоїсті змінні і ; для цих змінних складаються обмеження з рівностей і нерівностей

(1.26)

Причому змінні мають довільні знаки, а змінні

П

(1.27)

отрібно визначити такі значення змінних які б задовольняли умовам (1.26) і мінімізували форму

Коефіцієнти в лівій частині (1.26) отримуються транспонуванням матриці системи (1.24).

Вектор який задовольняє обмеженням основної задачі називається допустимим вектором, а основна задача - допустимою задачею. Допустимий вектор, який максимізує (1.25) називається оптимальним вектором, а задача - оптимальної. Така ж термінологія застосовується для двоїстої задачі.

Для кожної з цих задач можливі три випадки:

- є оптимальні вектори (а отже і допустимі);

- є допустимі вектори, але немає оптимальних;

- немає допустимих векторів.

О

(1.28)

сновна теорема двоїстості стверджує, що

Припустимо, що основна, а отже і двоїста задача має допустимі вектори.

П

(1.29)

окажемо, що

Нехай w і  допустимі вектори, тоді

(1.30)

Т

(1.31)

ому що для тих змінних , які приймають значення любого знака, виконуються рівності

(2.31)

а для невід'ємних змінних справедливими є нерівності

(1.32)

Якщо якась j-та нерівність двоїстої задачі не обертається в точну рівність (є суворою нерівністю), тобто

то рівність в формулі (1.30) для допустимих рівнянь можлива тільки при умові, що відповідна j-та змінна основної задачі обертається в нуль, тобто .

Ця вимога є необхідною і достатньою. Умовно це можна представити таким чином:

(1.33)

Це положення називають другою теоремою двоїстості [4, 5, 29] і формулюють таким чином. Для того, щоб допустимі розв'язки W і  пари двоїстих задач обертали в рівність співвідношення (1.30) тобто були оптимальними, необхідно і достатньо виконання наступної умови: якщо якась з нерівностей системи обмежень однієї задачі не обернулась в точку рівність то відповідна змінна іншої задачі повинна дорівнювати нулю. Аналогічним чином

(1.34)

тому що для тих змінних , які мають любий знак, справедливими є рівності

(1.35)

Якщо для деякого і в (1.35) виконується знак рівності, то необхідно і достатньо, щоб

Це положення умовно можна позначити таким чином:

(1.36)

Доведено наступні: для того, щоб допустимі розв'язки W і  пари задач обертали (1.34) в рівність (були оптимальними) необхідно і достатньо виконання наступної умови: якщо якась із змінних однієї з двоїстих задач суворо позитивна, то відповідне обмеження іншої (основної) задачі повинно обертатися в рівність. Із порівняння (1.30) і (1.34) виходить, що

(1.37)

Рівність в (1.37) можлива тоді і тільки тоді, коли виконуються умови (1.33) і (1.36).

Теорему про максимальний потік можна отримати з теореми двоїстості Теорема двоїстості, теорема про максимальний потік і теорема про мінімальне в теорії ігор – це різні формування одного і того ж положення. Розглянемо рівняння, які визначають максимальний потік, і складемо для них двоїсту задачу:

(1.38)

(1.39)

.

Неважко переконатися в тому, що матриця коефіцієнтів лівої частини співпадає з матрицею інциденцій.

Співставимо з равенствами (1.38) величини (всього їх N+2, де N – число внутрішніх вершин мережі), а нерівностям (1.39) – величини Нагадаємо, що

Тоді у відповідності з формальними правилами побудови двоїстої задачі отримаємо:

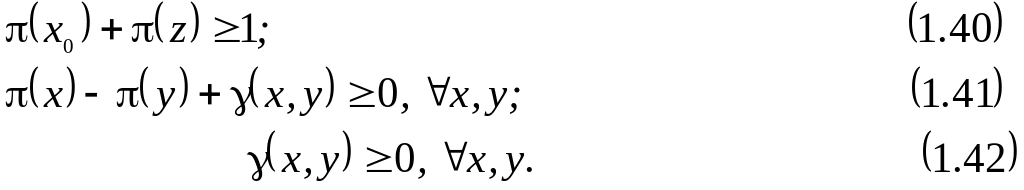
При цих обмеженнях потрібно знайти мінімум лінійної форми

(1.43)

Пояснимо це на прикладі

Приклад 3. неважко переконатися, що для мережі, яка зображена на рис. 5, матриця інциденцій має вигляд:

(1.44)

	(х0, x)	(х0, y)	(х, y)	(y, x)	(х, z)	(y, z)
х0	1	1	0	0	0	0
х	-1	0	1	-1	1	0
у	0	-1	-1	1	0	1
z	0	0	0	0	-1	-1

Р

Рис. 5. Пояснення до прикладу 3.

ядки матриці інциденцій відповідають вершинам, стовпчикам, дугам. Якщо дуга виходить з вершини, то на перетині відповідних рядка і стовпчика стоїть +1, якщо входить, то стоїть –1. Коли вершини неінцедентні, тобто не є ні початковою ні кінцевою вершиною дуги, то ставиться нуль. Дамо пояснення до співвідношень (1.40) – (1.44). По-перше, так як лінійна форма основної задачі залежить від величини , включимо її в невідомі, перенесли в ліву частину в співвідношеннях (1.38) і добавив в матриці інциденцій відповідний стовпчик

Тоді матриця коефіцієнтів перепишеться в вигляді

	(х0, x1)	(х0, y)	(х, y)	(y, x)	(х, z)	(y, z)	φ
х0	1	1	0	0	0	0	-1
х	-1	0	1	-1	1	0	0
у	0	-1	-1	1	0	1	0
z	0	0	0	0	-1	-1	1
	1	0	0	0	0	0	0
	0	1	0	0	0	0	0
	0	0	1	0	0	0	0
	0	0	0	1	0	0	0
	0	0	0	0	0	0	0
	0	0	0	0	1	1	0

В останню матрицю добавлено шість рядків, які відповідають нести рівнянням­ – обмеженням на пропускну спроможність. Випишемо кілька рівнянь, які відповідають рівнянням (1.45) в розвернутому вигляді.

Для х = х₀ друга сума в (1.38) не дає ні одного члена;

Для х ≠ х₀, z друга сума дає два члени. Тоді (1.38) буде мати вигляд:

Якщо транспортувати матрицю (1.45) і врахувати, що відповідає першому рівнянню в (1.46), а – останньому, то отримаємо рівняння (1.40).

Одиниця в правій частині (1.40) стоїть тому, що відповідний коефіцієнт лінійної форми дорівнює одиниці.

Можна показати, що якщо – мінімальний розріз, який відділяє х₀ від z, то оптимальний розв’язок двоїстої задачі дається формулами

(1.47)

(1.48)

Цікаво відмітити, що розв’язки (1.47) і (1.48) дають: розв’язок двоїстої задачі – мінімальний розріз,

розв’язок прямої задачі – максимальний потік.