1.1.3. Теорема про максимальний потік (теорема Форда-Фалкерсона)

Фордом і Фалкерсоном доведена фундаментальна теорема, яка має дуже велике значення в теорії графів, яка стверджує, що в любій мережі максимальне значення сумарного потоку на кінцевих дугах дорівнює мінімальній пропускній спроможності розрізу.

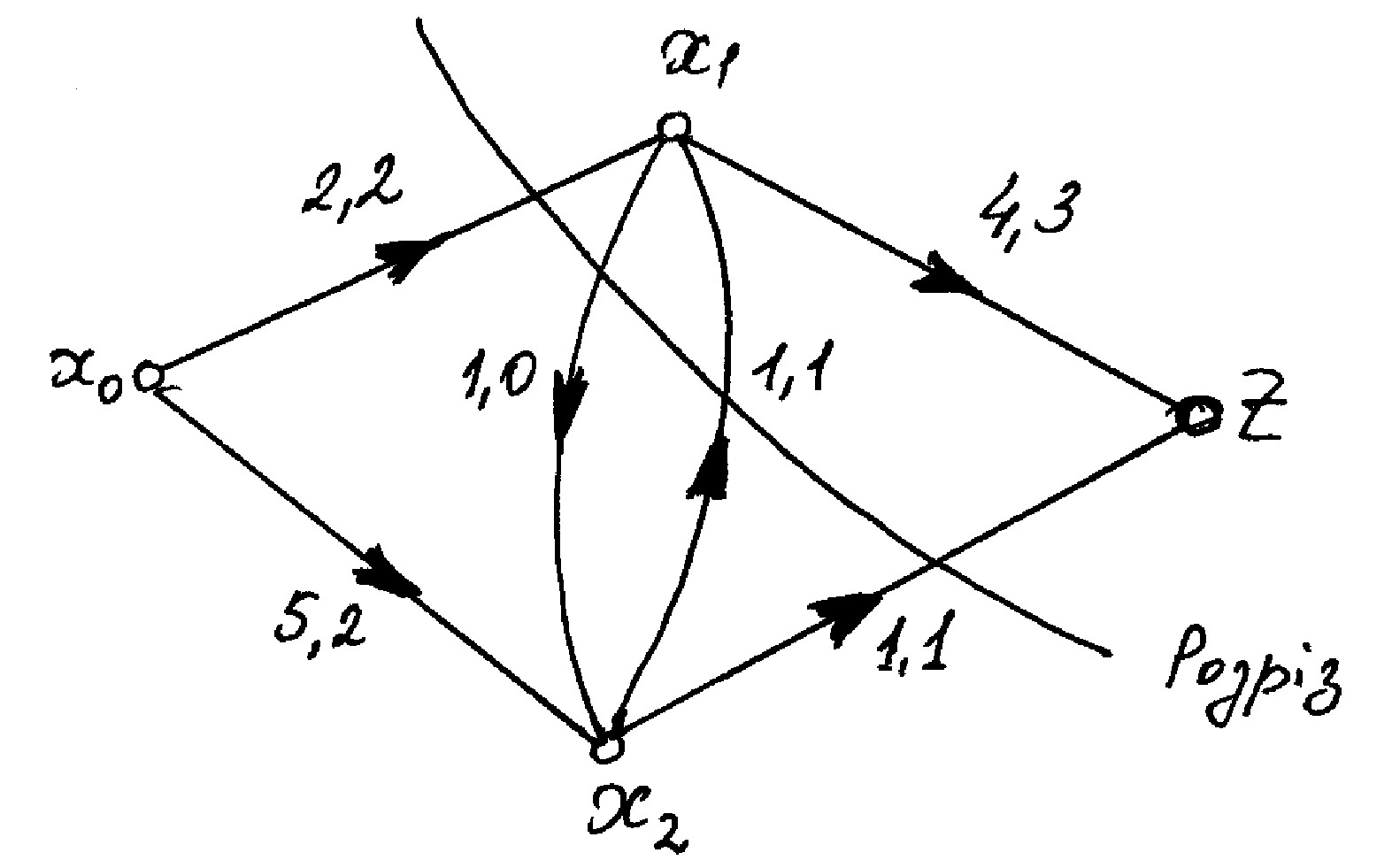
Рис. 2. Пояснення до прикладу 2.1.

Приклад 2.1. На рис. 2 наведена мережа, яка складається з чотирьох вершин і шести дуг. На кожній дузі проставлена її пропускна спроможність (перша цифра) і потік (друга цифра). З малюнку видно, що для проміжних вершин х₁ і х₂ умови збереження потоку виконуються, Ф=4. Можна знайти розріз, пропускна спроможність якого Г=4. Цей розріз складається з дуг (х₀, х₁), (х₂, х₁), (х₂, х_z). Дуга (х₁, х₂) в розріз не входить.

Потік на кінцевих дугах – максимальний, а пропускна спроможність розміру – мінімальна. Наприклад, пропускна спроможність розрізу 1 – Г=5, а розрізу 2 – Г=10.

Розглянемо доведення теореми про максимальний потік. Необхідно знайти такий розріз

, щоб для

(1.11)

(1.12)

Співвідношення (1.12) можна пояснити таким чином. Ясно, що максимальний потік в розрізі буде тоді, коли в нього поперед всього включаються пари вершин, які або не мають зворотних дуг, або мають нульове значення потоку по зворотній дузі (рис. 2), тому що любе значення потоку по зворотній дузі зменшує сумарний потік між двома вершинами і він не буде максимальним.

Якщо ввести позначення

(1.13)

(1.14)

(1.15)

то вважаючи, що Х=Р, а , співвідношення (1.11) і (1.12) можна переписати у вигляді

(1.16)

(1.17)

Якщо для вибраного максимального потоку буде знайдений розріз з такими властивостями, то теорема про максимальний потік буде доведена. Максимальний потік * в мережі завжди існує, тому що значення дугового потоку завжди обмежене і дискретне, отже, існує скінчений набір значень потоку в мережі (при скінченій кількості дуг). З яких завжди можна вибрати по крайній мірі одне максимальне значення потоку в мережі.

Вважаючи, що максимальний потік в мережі φ* заданий, визначимо множину Х наступним рекурентним чином:

(1.18)

(1.19)

Проаналізуємо процедуру (1.19). В мережі, на дугах якої задані максимальні потоки, виділимо під мережу, виключив прямі дуги (х, у), де потоки досягають максимальних значень, що дорівнюють пропускним спроможностям С (х, у). На рис. 3 наведені можливі локальні структури мережі.

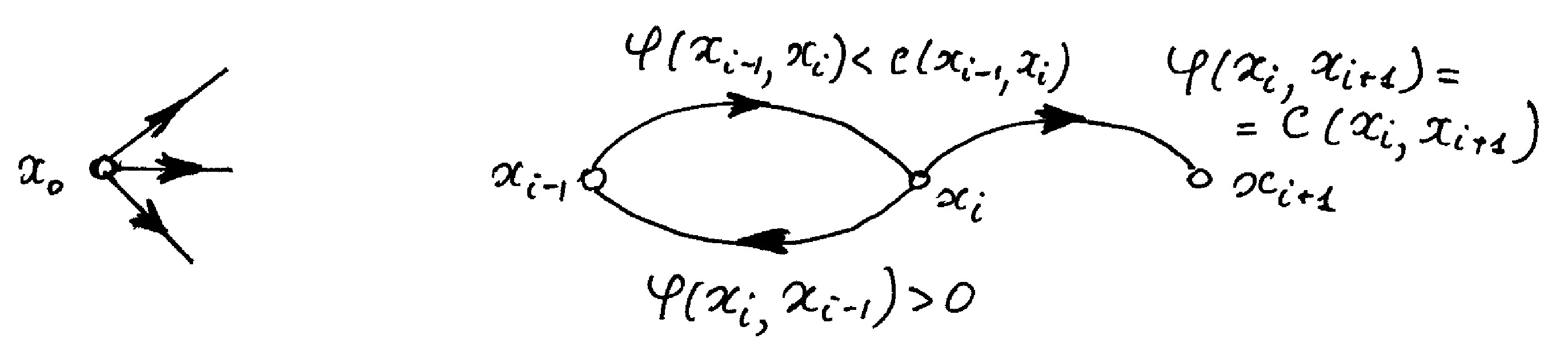
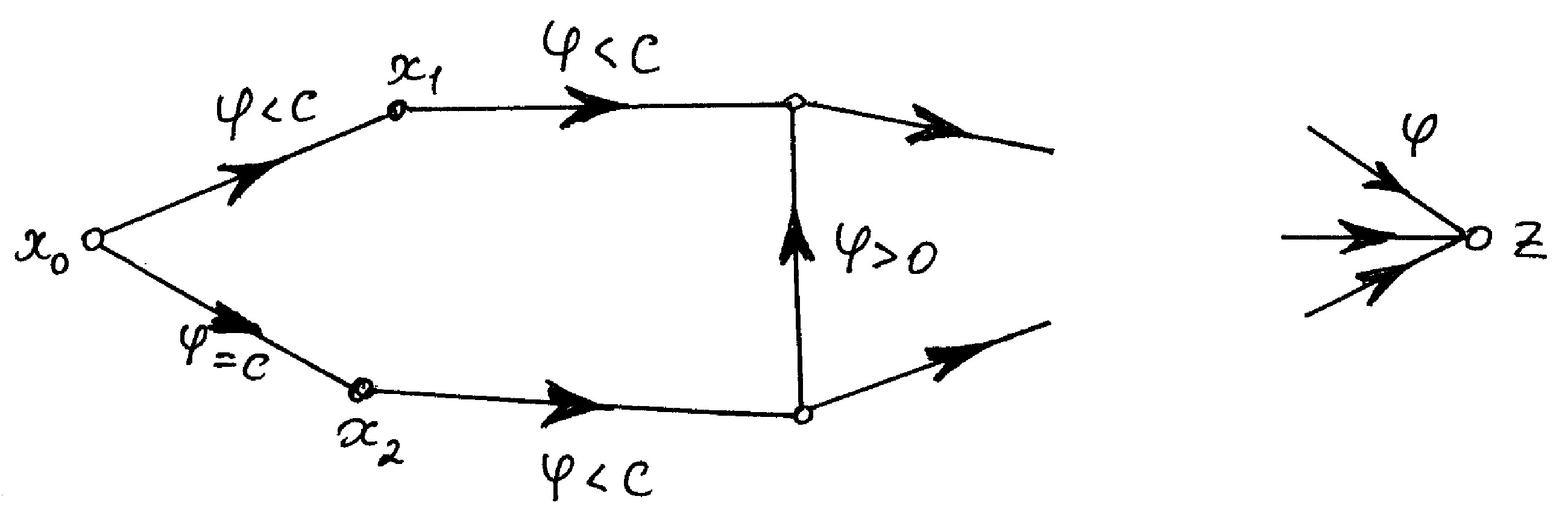
Рис. 3. Локальні структури мережі

На рис. 3а показано вхід мережі. На рис. 3 б, в, г показані внутрішні ділянки мережі, які з'єднують вершини. У відповідності до правил (1.19) дуга (х_і, Х_і+1) на рис. 3 б виключається і вершина Х_і+1 не попадає в множину X; вершина Х₂ на рис. 3 в, не попадає, а вершина Х₄ - попадає в множину X, тому що Х₃ є Х.

Стверджується, що кінцева вершина

z  X. (1.20)

Д

(1.21)

оводиться це методом від зворотнього [29], припустимо, що це не так. Тоді із визначення множини Х витікає, що існує шлях з вершини x₀ в вершину Z, тобто

Який на рис. 4 має ту властивість, що для прямих дуг цієї мережі.

(1.22)

а для зворотних буде

Рис. 4. Пояснення до теореми про максимальний потік

Позначимо через ₁ мінімум різниці який береться по всім прямим дугам цього шляху, а через ₂ – мінімум по всім зворотнім дугам. Введемо величину . Змінимо потік , збільшивши його на  на всіх прямих дугах шляху, тобто і зменшивши його на цю величину на всіх зворотних дугах, тобто .

В цьому випадку величина сумарного потоку на кінцевих дугах мережі, яка була Ф складає

(1.23)

Але (1.23) суперечить тій умові, що потік в мережі  є максимальним. Таким чином (1.20) доведено, отже доведена теорема про максимальний потік.

З цього факту випливає важливий наслідок:

Потік  є максимальним в тому і тільки в тому випадку, якщо нема ні одного шляху, який збільшує його.

Цей наслідок дає ефективний засіб визначення максимального потоку. Для того, щоб потік зробити максимальним, необхідно наситити всі дуги розрізу .