Тема 3. Теория пар сил

Момент силы относительно центра. Опыт показывает, что эффект действия силы, приложенной к телу (например, к рычагу, штурвалу), на разных расстояниях от точки закрепления тела, зависит от так называемого момента силы относительно точки закрепления.

Моментом силы относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы:

M₀( ) = ± Fh, (3.1.6)

где h – кратчайшее расстояние от центра О до линии действия силы .

Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 3.1.24, 3.1.25). Момент силы измеряется в Н·м.

М омент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо равно нулю).

Графически абсолютная величина момента силы относительно центра О выражается удвоенной площадью ΔОАВ:

M₀ ( ) = 2S ∆ОАВ. (3.1.7)

М омент силы относительно центра как векторное произведение. Введенного понятия «момент силы относительно центра как алгебраическая величина» оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие «момент силы относительно центра как вектор», модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.

Вектор момента силы прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 3.1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором и найдем векторное произведение .

По определению векторного произведения

| |= 2S∆ОАВ.

Модуль вектора момента силы также равен удвоенной площади ∆ОАВ.

Тогда

= .

Направление векторного произведения также совпадает с направлением вектора момента. Следовательно, вектор-момент силы относительно центра О можно рассматривать как векторное произведение радиус-вектора , проведенного из этой точки в точку приложения силы, на вектор силы :

(3.1.8)

Момент силы относительно оси. Чтобы охарактеризовать вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг некоторой оси, вводится понятие «момента силы относительно оси».

Р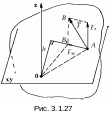 ассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.3.1.27). Пусть на тело действует сила , приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу на две составляющие: , параллельную оси OZ, и , лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой ,будет вызван ее составляющей _.

M_z ( ) = M₀ ( ) = ± F_xy h = ± 2S ∆OAB₁. (3.1.9)

Моментом силы относительно оси называют момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Момент силы относительно оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию F_xy, стремящейся вращать плоскость XY вокруг оси Z в сторону, противоположную вращению часовой стрелки.

Момент силы относительно оси равен нулю:

1) если F_xy = 0, т.е. линия действия силы параллельна оси OZ;

2) если h = 0, т.е. линия действия силы пересекает ось OZ.

Следовательно, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

П ара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил называется парой сил (рис. 3.1.28).

Пара сил не имеет равнодействующей, и силы пары не уравновешиваются. Действие пары на тело характеризуется ее моментом:

1) вектор-момент перпендикулярен плоскости действия пары;

2) направлен в ту сторону, чтобы, смотря с его конца, вращение было происходящим против хода часовой стрелки;

3) величина вектора равна в выбранном масштабе численному значению момента пары.

Вектор-момент пары равен векторному произведению радиуса-вектора на ту из сил пары, к началу которой направлен вектор :

, (3.1.10)

или

, (3.1.11)

по модулю

M = r Fsin α = Fh; M =  Fh. (3.1.12)

Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары:

. (3.1.13)

Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты этих пар сил, направленные по одной прямой, складываются алгебраически.

М омент пары сил, эквивалентный системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар (рис. 3.1.29):

, (3.1.14)

где M_i = ± F_i d_i .

Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю:

= 0.

С иловое воздействие на ВС часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) моментом винта М_в (рис. 3.1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен ВС. Этот момент уравновешивают некоторым отклонением элеронов; аэродинамические силы _Э._пр и _Э.._лев составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению.