Тема 2. Система сходящихся сил

Сложение сходящихся сил. Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

Сложить две или несколько сил – значит заменить эти силы одной силой, им эквивалентной, т.е. найти их равнодействующую (рис. 3.1.16).

Из ∆ADC: т.к. cos(180 – ) = –cos, то получим

, (3.1.2)

. (3.1.3)

Найти равнодействующую можно также, построив половину параллелограмма – треугольник сил, в котором равнодействующая является замыкающей стороной (рис. 3.1.17).

Р авнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (рис. 3.1.18).

Так как , а , то .

Равнодействующая нескольких сходящихся сил выражается по модулю и направлению вектором, соединяющим начальную и конечную точки ломаной линии (правило силового многоугольника) (рис. 3.1.19).

или . (3.1.4)

Сходящиеся силы уравновешиваются в случае, если их равнодействующая равна нулю, т.е. многоугольник сил замкнут. Конец вектора последней силы совпадает с началом вектора первой силы, все силы направлены по контуру многоугольника в одну сторону, т.е. .

Согласно, аналитическому условию равновесия при R = 0 получим

,

где ∑ F_ix, ∑ F_iy, ∑ F_iz – проекции сил на координатные оси. Следовательно,

∑ F_ix = 0; ∑ F_iy = 0; ∑ F_iz = 0. (3.1.5)

Для равновесия тела при действии на него пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из координатных осей была равна нулю.

Теорема о равновесии трех непараллельных сил. Линии действия трех непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке. К твердому телу в точках А₁, А₂, А₃ приложены три непараллельные взаимно уравновешивающиеся силы лежащие в одной плоскости. Перенесем силы и в точку О и найдем их равнодействующую. Сила будучи уравновешивающей системы сил и , равна по модулю их равнодействующей и направлена по линии ее действия в противоположную сторону (рис. 3.1.20).

С ходящиеся силы, приложенные к ВС. Часто для качественной оценки сил, действующих на ВС, их представляют в виде сходящихся сил. Равнодействующую сил давления воздушного потока на крыло и сил трения протекающего воздуха о его поверхность можно считать суммой двух сходящихся сил (рис. 3.1.21):

,

где – аэродинамическая сила крыла;

– сила лобового сопротивления;

– аэродинамическая подъемная сила крыла.

В виде сходящихся сил представляют часто и силы, действующие на ВС в полете. При наборе высоты, например, в упрощенную систему действующих на ВС сходящихся сил входят (рис. 3.1.22):

– сила тяжести (вес самолета);

– тяга винта (или газотурбинного двигателя);

– сила лобового сопротивления самолета;

– аэродинамическая подъемная сила.

Аналогичным образом упрощают систему сил, действующих на ВС и в других режимах полета.

П 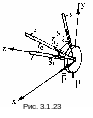ример. Ось колеса шасси легкого самолета крепится к фюзеляжу с помощью трех шарнирно закрепленных подкосов (рис. 3.1.23), оси которых пересекаются в точке О. Ось подкоса 1 совпадает с осью колеса, подкос 2 расположен в горизонтальной плоскости под углом  = 30° к оси первого подкоса, а подкос 3 – в вертикальной плоскости под углом  = 60°. На колесо действуют силы Р = 10 кН и F = 3 кН. Определите усилия в подкосах.

Решение. Рассмотрим равновесие колеса. На колесо действуют две активные силы ( и ) и наложены связи – невесомые стержни 1, 2, 3. Используя аксиому освобождаемости от связей, мысленно отбрасываем связи, заменяя их действие реакциями . Выбираем оси координат так, чтобы решение задачи было наиболее простым. Составляем условия равновесия колеса, находящегося под действием пространственной системы сходящихся сил :

∑ F_ix =0; – F – S₂ sin  = 0; S₂ = – 6 кН.

∑ F_iy =0; P + S₃ sin  = 0; S₃ = – 11,5 кН.

∑ F_iz =0; S₁ + S₂ cos  + S₃ cos  = 0; S₁ = 11 кН.

Освобождая тело от связей, мы полагали все стержни растянутыми. Знак «минус» в полученных значениях реакций S₂ и S₃ означает, что в действительности они сжаты.