Тема 8. Синтез механизмов

Основные понятия. В переводе с греческого слова synthesis буквально означает «сочетание, составление». В современной теории механизмов термин «синтез» означает «проектирование, создание».

Выделят две основные задачи синтеза:

1. Воспроизведение заданного закона движения, при этом требуется определить фиксируемые параметры звеньев (длины, координаты, массы, моменты инерции и т. п.).

2. Воспроизведение заданной траектории выходного звена, т.е. задача о положениях.

Методы синтеза:

• графические – методы, основанные на представлении механизмов и параметров их движения на чертежах. Графические способы дают наглядное представление о строении механизмов и закономерностях движения их звеньев, но отличаются погрешностями свойственными графическим методам;

• аналитические – методы, основывающиеся на различных методах математики и обеспечивающие более высокую точность определения искомых величин;

• графоаналитические – методы, объединяющие преимущества и недостатки графического и аналитического методов;

• экспериментальные – методы, основанные на изготовлении моделей и макетов проектируемых механизмов;

• синтез методами анализа:

• оптимальное проектирование:

• градиентные методы,

• метод случайного поиска,

• минимизация уступок,

• комбинированные методы,

• другие;

• автоматизирование проектирование.

Синтез рычажных механизмов. Синтез по положениям звеньев. Синтез передаточных и направляющих механизмов. Плоские рычажные механизмы широко распространены в современном машино- и приборостроении. Высокая технологичность изготовления, выполнение шарнирных соединений на подшипниках качения, надежность, долговечность – достоинства этих механизмов. Но они менее универсальны, чем кулачковые и зубчатые механизмы.

Первым этапом проектирования является выбор кинематической схемы механизма, которая обеспечивала бы требуемый вид и закон движения. Второй этап – разработка конструкторских форм механизма, обеспечивающих его прочность и долговечность. Третий этап – разработка технологических и технико-экономических показателей проектируемого механизма.

В теории механизмов и машин рассматриваются и решаются задачи первого этапа проектирования, на котором разрабатываются кинематические схемы механизмов, воспроизводящие требуемый закон движения. Проектирование механизма начинают с выбора структурной схемы при помощи справочных материалов или на основе анализа видов движения, которые должны быть реализованы. Этот этап проектирования называется структурным синтезом.

Следующий этап – кинематический синтез. Он заключается в определении геометрических параметров механизма с учетом основных кинематических функций, которые должен реализовывать механизм.

Структурный и кинематический синтезы дают возможность получить кинематическую схему механизма, отвечающую требованиям, предъявляемым к проектируемому механизму. Кинематические функции, которые должен реализовать проектируемый механизм, воспроизводятся им с определенной точностью. На основании анализа спроектированного механизма по степени точности воспроизведения заданной функции решают, пригоден ли полученный механизм или необходимо произвести корректировку предыдущих этапов проектирования с изменением исходных данных. Если и повторные расчеты не дают удовлетворительных результатов, то следует перейти к другой структурной схеме механизма и выполнить для нее соответствующие расчеты. Этот этап называют этапом точностного проектирования.

Таким образом, задача проектирования механизма является сложной, многопараметрической, причем число исходных параметров механизма, как правило, больше числа исходных данных, поэтому часть параметров приходится варьировать.

При синтезе механизмов приходится решать две основные задачи: воспроизведение заданных передаточных функций и воспроизведение заданных траекторий движения точек.

В зависимости от решаемой задачи рычажные механизмы делятся на следующие группы:

• передаточные механизмы – механизмы, реализующие заданную функциональную зависимость между положениями входного и выходного звеньев механизма или между их перемещениями, то есть механизмы, предназначенные для реализации требуемых передаточных функций;

• направляющие механизмы – механизмы, в которых точка на звене, совершающем сложное движение, перемещается при движении механизма по заданной траектории, то есть механизмы, предназначенные для воспроизведения заданных траекторий движения звеньев или их точек.

Пример 1. Рассмотрим синтез механизмов по заданным положениям звеньев на примере проектирования шарнирного четырехзвенника по двум крайним положениям коромысла (ведомого звена).

П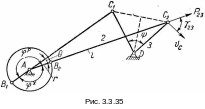 усть заданы крайние положения коромысла DC₁ и DC₂ и, следовательно, угол  его поворота (рис. 3.3.35); кривошип AB должен делать полный оборот. Точка А может быть выбрана произвольно. Соединяем ее с точками С₁ и С₂. Из чертежа следует:

АС₁ = l – r и АС₂ = l + r,

где r – радиус кривошипа АВ;

l – длина шатуна ВC.

Из рис. 3.3.35 следует, что

АС₂ – AC₁ = l + r – l + r = 2r,

Откуда

r = AB = .

Пример 2. Рассмотрим синтез кривошипно-ползунного механизма по средней скорости ползуна и частоте вращения кривошипа (рис. 3.3.36).

П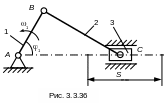 усть заданы средняя скорость ползуна (V_ср); частота вращения кривошипа (n₁); отношение длины шатуна ВС к длине кривошипа (АВ – ).

Необходимо определить длины звеньев L_АВ и L_ВС

1. За 1 мин ползун 3 проходит путь, равный , т.е. величина хода ползуна раходится по фомуле

.

2. Из рис. 3.3.36 длина кривошипа АВ равна половине хода ползуна 3 вычисляется по формуле

.

3. Длина шатуна определяется через заданное соотношение:

.

Методы оптимизации в синтезе механизмов с помощью ЭВМ. Оптимизация в синтезе механизмов – определение выходных параметров синтеза из условия минимума целевой функции при выполнении принятых ограничений.

При аналитическом синтезе пространственного механизма задача значительно усложняется. Математические модели механизмов отображаются уравнениями или неравенствами, в которых фигурируют независимые переменные.

Если основное уравнение в синтезе определено некоторой целевой функцией

Z = f(X₁, X₂, ... , X_n),

где Х₁, Х₂, ... Х_n – параметры синтеза механизма (входные и выходные), то дополнительные условия называются ограничениями, например,

_i (Х₁, Х₂,..., Х_n) { , = , } b_i ( =1, 2, 3, ... n).

Часто при постановке задачи синтеза механизмов требуется обеспечить экстремальное значение целевой функции. Например, если Z определяет среднее отклонение траектории, описываемой точкой звена синтезируемого механизма от заданной траектории, то ставится требование обеспечения минимума функции Z.

К ограничениям относятся условия существования кривошипов, обеспечение требуемых габаритных размеров, обеспечение заданного КПД, механизма, заданного ритма движения точки вдоль кривой, заданного отношения скоростей звеньев и т.п.

При постановке задач синтеза пространственных механизмов возникает необходимость обеспечения оптимальных наилучших значений функционалов, зависящих от многочисленных параметров механизмов. Это зачастую сложнейшая аналитическая задача. Для поиска оптимальных решений используются ЭВМ.

Многочисленные методы поиска решений могут быть объединены в три основные группы:

• методы случайного поиска;

• методы направленного поиска;

• методы комбинированного поиска.

Случайный поиск реализуется в следующей последовательности:

1. Выбор некоторых значений входных параметров синтеза из набора случайных чисел и проверка их допустимости по ограничениям, которые должны быть приняты по условиям задачи.

2. Вычисление и запоминание значений целевой функции по значениям входных параметров, удовлетворяющих поставленным ограничениям, запоминание этих параметров ЭВМ.

3. Выбор новых случайных значений входных параметров синтеза и проверка их допустимости по поставленным ограничениям.

4. Вычисление значений целевой функции по новым допустимым значениям входных параметров и сравнение нового значения целевой функции с предыдущими.

Если это новое значение целевой функции больше предыдущего при поиске максимума или меньше предыдущего при поиске минимума, то оно вводится в память машины вместе с соответствующими значениями входных параметров, а предыдущие устраняются из памяти.

Направленный поиск в отличие от случайного осуществляется по некоторым выбираемым направляющим.

Комбинированный поиск используется при высокой размерности пространства, когда количество стационарных точек велико, и их исследование и классификация практически невозможны. В таких ситуациях целесообразно комбинировать методы поиска, например, применять для зондирования пространства случайный поиск, а для уточнения оптимумов – направленный.

Синтез зубчатых механизмов. Зубчатые передачи с неподвижными осями колес. Передаточное отношение зубчатой передачи – отношение угловой скорости вала, принятого за входной, к угловой скорости вала, принятого за выходной

.

Зубчатые передачи могут быть одноступенчатыми и многоступенчатыми.

Передаточное отношение многоступенчатой передачи равно произведению передаточных отношений отдельных ступеней:

.

Одноступенчатые передачи делятся на передачи с внешним зацеплением (рис. 3.3.37, а) и с внутренним зацеплением (рис. 3.3.37, б).

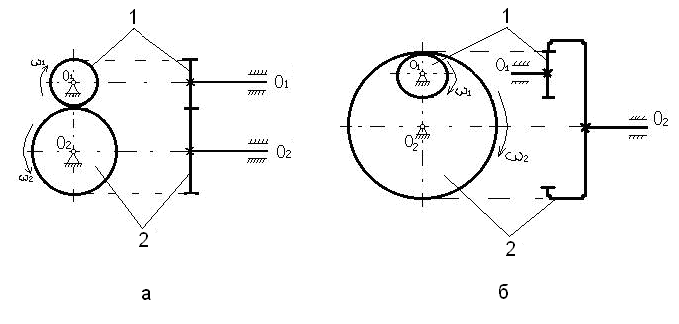
Рис. 3.3.37

Для внешнего зацепления

.

Для внутреннего зацепления

.

Имея схему передачи и зная числа зубьев или радиусы начальных окружностей колес, можно всегда определить общее передаточное отношение.

Синтез планетарных передач. Планетарные передачи имеют колеса с подвижными осями, которые называются сателлитами.

Водило – подвижное звено, в котором закреплена ось сателлита.

Центральное колесо – колеса, геометрические оси которых неподвижны.

Опорное колесо – неподвижное центральное колесо.

Примеры планетарных механизмов приведены на рис. 3.3.38.

Определение передаточного отношения по формуле Виллиса рассматривалось в кинематическом анализе зубчатых механизмов, запишем их для схем, приведенных на рис. 3.3.38:

• для одноступенчатого механизма (рис. 3.3.38, а)

.

• для многоступенчатого механизма (рис. 3.3.38, б)

,

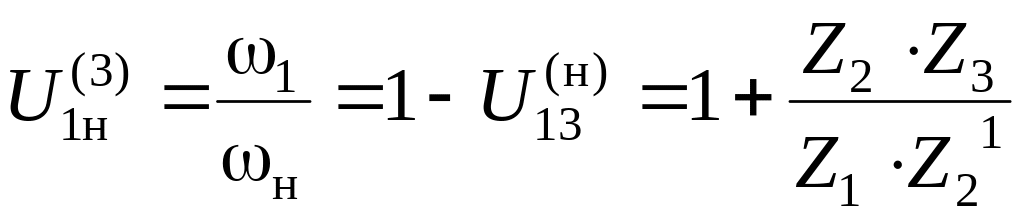где – передаточное отношение планетарной передачи от входного колеса 1 к выходному звену Н (водилу) при неподвижном колесе 3;

– передаточное отношение зубчатой передачи от входного звена 1 к выходному звену 3 при неподвижном звене Н.

Р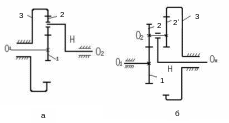 ис. 3.3.38. Схемы планетарных механизмов:

а – одноступенчатый механизм, 2-2 – блок сателлитов; б – двухступенчатый:

1 – центральное колесо; 2 – сателлиты; H – водило

Для определения чисел зубьев планетарной передачи вводятся дополнительные условия, при которых решение задачи было быть однозначным:

1. Числа зубьев Z₁, Z₂, Z₃, ... , Z_n должны быть целыми числами, а модули всех колес одинаковыми.

2. Все зубья колес должны быть нулевыми (неисправленными), т.е. Z₁  Z_min = 17 (для избежания подреза ножки зуба) для колес с внешним зацеплением; для колес с внутренним зацеплением Z₃  Z_min = 85, в обоих случаях Z₂ =  20.

3. Условие соосности – оси центральных колес и водила должны совпадать между собой:

• для одноступенчатого механизма:

Z₁ + 2Z₂ = Z₃;

• для многоступенчатого механизма:

Z₁ + Z₂ = Z₃ – ;

4. Условие соседства: сателлиты должны быть расположены с таким окружным шагом, чтобы между окружностями вершин соседних сателлитов обеспечивался гарантированный зазор:

sin  (Z₂ + 2)/(Z₁ + Z₂),

где k – число сателлитов.

Для схемы б вместо Z₂ следует подставить , если  Z₂.

5. Условие сборки: сборка сателлитов должна осуществляться без натягов при равных окружных шагах между ними. Это возможно при выполнении следующего условия:

= C,

где С = 1, 2, ... – целое число.

Синтез механизмов по методу приближения функций. Большинство задач синтеза механизмов могут быть решены только в приближенной форме, поэтому кроме метода параметрической оптимизации, используют методы теории приближения функций: метод наилучшего приближения функций, предложенный П.Л. Чебышевым, различные методы интерполирования функций, метод квадратичного приближения функций, метод использования взвешенной разности, предложенный Н.И. Левитским. Метод приближения функций является общим методом синтеза механизмов, применимым ко всем типам механизмов. Эти методы рассмотрены в специальных разделах теории механизмов и машин.