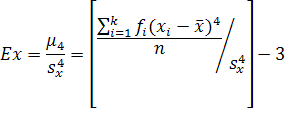6.1 Визначення коефіцієнту спадкування в однофакторному комплексі
Припустимо‚ необхідно знайти спадкування жирномолочності в потомстві трьох биків-плідників: Променя‚ Вітру та Алмазу. Для цього спочатку складають однофакторний дисперсійний комплекс (таблиця 14)‚ у градації якого записують показники жирномолочності дочок.
Підраховують суму варіант Σx за графами таблиці‚ визначають середні арифметичні в групі дочок кожного бика:
;
за всією вибіркою
:
.
Після цього визначаємо дисперсію (суму квадратів):
- генотипічну дисперсію(Cγ = Сх) (міжгрупова сума квадратів) – показник генотипічного різноманіття жирономолочності батьків за формулою:
Cγ = Σni (Xi -XΣ)2‚ (37)
Cγ = 5 (+0‚25)2 + 5 (-0‚05)2 + 5 (-0‚21)2 =0‚5455;
-паратипічну дисперсію (Cπ ) (внутрішньогрупова сума квадратів) – показник різноманіття дочок биків за жирномолочністю за формулою:
Cπ = Σ (x - Xi)2 (38)
Cπ = (-0‚1)2 +(-0‚1)2 +(+0‚1)2 + … +(+0‚06)2 +(+0‚06)2 =0‚152;
-фенотипічну дисперсію (Cφ) – показник загального фенотипічного різноманіття ознаки за формулою:
Cφ = Σ (x –XΣ)2 (39)
Cφ = (+0‚15)2 +(+0‚15)2 +(+0‚25)2 +(+0‚35)2 + … + (-0‚15)2 +(+0‚15)2 =0‚6975.
Cφ = Cγ + Cπ
Cφ = 0‚5455 + 0‚152 = 0‚6975.
Коефіцієнт спадковості визначають за формулою:
h2 =
(40)
Обчислюють також критерій достовірності спадкування за формулою:
F=
(41)
F=
=2,2
ν1 = r – 1 = 3 – 1 = 2
ν2 = N - r = 15 – 3 = 12
Fst = 3.9 –6.9 – 12.3
Тема 7. Непараметрична статистика
Правильне застосування параметричних критеріїв для перевірки статистичних гіпотез ґрунтується на припущенні про нормальний розподіл сукупностей, з яких взяті порівнювані вибірки. Однак це не завжди має місце, так як не всі біологічні ознаки розподіляються нормально. Також важливим фактором, що обмежує застосування критеріїв, заснованих на припущенні нормальності, є обсяг вибірки. До тих пір поки вибірка досить велика (наприклад, 100 або більше спостережень), можна вважати, що вибірка розподілена нормально, навіть якщо немає впевненості, що розподіл змінної в популяції є нормальним. Тим не менш, якщо вибірка мала, ці критерії слід використовувати тільки при наявності впевненості, що змінна дійсно має нормальний розподіл.
Важливим є і та обставина, що у біологічних дослідженнях досліднику дуже часто доводиться мати справу не тільки з кількісними, а ще й з якісними ознаками, багато з яких виражаються порядковими номерами, індексами та іншими умовними знаками. У таких випадках необхідно використовувати непараметричні критерії.
а |
|
а |
б |
Приклад даних, які: а - підлягають закону нормального розподілення, б - не підлягають закону нормального розподілення
|
|
7.1 Перевірка гіпотез про закон розподілу. Застосування коефіцієнтів асиметрії та ексцесу для перевірки нормальності розподілу
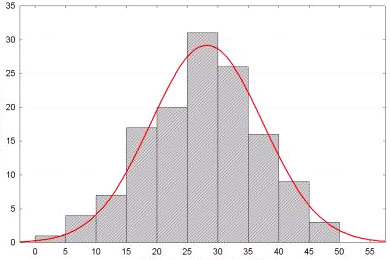
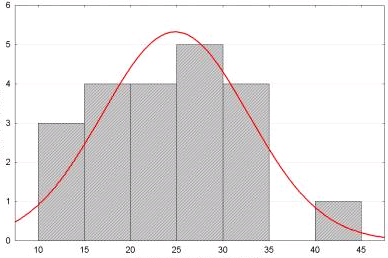
Емпіричний варіаційний ряд і його графік – варіаційна крива – найпростіші методи оцінки нормальності розподілу даних, але все ж вони не дозволяють із повною упевненістю судити про закон розподілу сукупності, з якої взята вибірка. На величині будь-якої ознаки, що змінюється, позначається вплив численних, в тому числі і випадкових, факторів, що спотворюють чітку картину варіювання. Між тим знання закону розподілу дозволяє уникнути можливих помилок в оцінці генеральних параметрів за вибірковими характеристиками.
Гіпотезу про закон розподілу можна перевірити різними способами, зокрема за допомогою коефіцієнтів асиметрії As і ексцесу Ex. При нормальному розподілі ці показники дорівнюють нулю. Насправді така рівність майже не спостерігається. Асіметрію та ексцес вибірки визначають зазвичай за такими формулами:
|
(42) |
|
(43) |
Для перевірки нормальності розподілу за значеннями цих коефіцієнтів застосовують таблиці (див. Додатки, табл. 4 і 5). У них зазначені критичні точки для різних рівнів значимості α та обсягів вибірки n. Якщо коефіцієнти As і Ех перевершують критичні точки, які наведені в цих таблицях, гіпотеза про нормальність розподілу повинна бути відкинута.
Розбір вирішення задач
На практичних заняттях студентам було запропоновано виміряти в міліметрах довжину відібраних навмання 200 хвоїнок сосни звичайної. В результаті був отриманий варіаційний ряд, за яким розраховували значення показників асиметрії та ексцесу.
Довжина хвої xi, мм |
Частоти fi |
а |
fia |
fia2 |
fia3 |
fia4 |
125 |
2 |
–6 |
–12 |
72 |
–432 |
2592 |
175 |
2 |
–5 |
–10 |
50 |
–250 |
1250 |
225 |
4 |
–4 |
–16 |
64 |
–256 |
1024 |
275 |
5 |
–3 |
–15 |
45 |
–135 |
405 |
325 |
7 |
–2 |
– 14 |
28 |
–56 |
112 |
375 |
25 |
–1 |
–25 |
25 |
–25 |
25 |
425 |
39 |
0 |
0 |
0 |
0 |
0 |
475 |
46 |
+1 |
+46 |
46 |
+46 |
46 |
525 |
31 |
+2 |
+62 |
124 |
+248 |
496 |
575 |
23 |
+3 |
+69 |
207 |
+621 |
1863 |
625 |
13 |
+4 |
+52 |
208 |
+832 |
3328 |
675 |
2 |
+5 |
+ 10 |
50 |
+250 |
1250 |
725 |
1 |
+6 |
+6 |
36 |
+216 |
1296 |
Сума (Σ) |
200 |
— |
+153 |
955 |
+ 1059 |
13687 |
Визначаємо Σ fia, Σ fia2, Σ fia3, Σ fia4.
Користуючись підсумками таблиці, визначаємо: b1 = 153 / 200 = 0,765; b2 = 955/200 = 4,775; b3 = 1059/200 = 5,295 і b4 = 13687/200 = 68,435, а також b12 = 0,5852; b13 = 0,4477; b14 = 0,3425; 2b12= 0,8954; 3b14 = 1,0274; 3b1 b2 = 10,9586; 6b12 b2 = 16,7660 і 4b1b3 = 16,2027.Знаходимо: sx2 = b1– b2 = 4,775 – 0,5852 = 4,1898; sx = 2,0469; sx3 = 8,5761 і sx4 = 17,5544. Переходимо до визначення центральних моментів розподілу: μ3 = 5,295 – 10,9586 + 0,8954 = –4,7682; μ4 = 68,4350 – 16,2027 + 16,7660 – 1,0274 = 67,9709. Звідси As = –4,7682 / 8,5761 = – 0,5560 і Ex = 67,9709 / 17,5544 – 3 = 3,8720 – 3 = 0,8720. Отримані величини As і Ех показують, що даний розподіл має лівосторонню асиметрію і помітно виражений ексцес.
Далі, для α = 1% і n = 200 в табл. 4 знаходимо Asst = 0,403, а в табл. 5 - Exst = 0,832. Так як емпірично обраховані величини As і Ех перевищують табличні критичні значення, можна зробити висновок про наявність у цього розподілу значимих асиметрії та ексцесу, тобто отримані дані не розподілені нормально.