8.8.3. Скорость всплытия газового пузырька в жидкости

Свободный газовый пузырь в жидкости, или капля одной жидкости в другой жидкости при отсутствии эффекта смешения, имеет одну определенную геометрическую характеристику – объем V. Форма пузыря и его линейные характеристики могут изменяться под действием динамических сил и силы поверхностного натяжения на границе раздела фаз (компонент).

Таким образом, в качестве линейного масштаба можно вводить или величину V^1/3, или эффективный радиус:

(8.94)

Свободное движение пузыря обусловлено подъемной силой порядка и силой гидродинамического сопротивления порядка , здесь – коэффициент гидродинамического сопротивления пузыря; – скорость свободного всплытия пузыря.

Определяемый критерий в форме числа Фруда:

(8.95)

где – относительная разность плотностей.

В критериях надо брать модуль величины относительной плотности . Если , то пузырь (капля) всплывает, если – капля тонет.

Обычно связь между подъемной силой и гидродинамическим сопротивлением записывают в форме, соответствующей стационарному обтеканию правильной сферы:

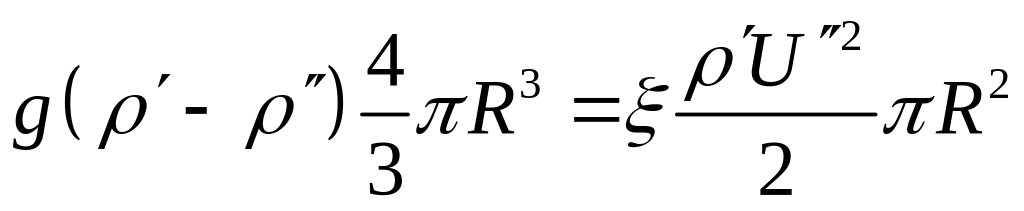(8.96)

При такой записи

, (8.97)

т.е. по существу, это один и тот же критерий подобия.

Практически удобнее пользоваться корнем квадратным из критерия Фруда, который обозначим символом безразмерной скорости всплытия пузыря:

(8.98)

На границе раздела возникает гидродинамическое взаимодействие, вызывающее образование поля давления. Это приводит к деформациям и осцимациям² поверхности пузыря.

В качестве меры этой деформации поверхности раздела принимается критерий, характеризующий взаимодействие подъемной силы и давления, создаваемого поверхностным натяжением:

(8.99)

Молекулярные вязкости жидкости и газа проявляются в условиях преобладания ламинарного характера течения, т.е. при относительно малых числах Рейнольдса:

(8.100)

При этом следует учитывать критерий Архимеда:

(8.101)

и симплекс³ (8.102)

Если в пузыре существенно выражены динамические эффекты, то в качестве самостоятельной величины учитывается симплекс:

(8.103)

В реальных ситуациях действие симплексов (8.102) и (8.9103) практически не проявляется.

Для сферы с неподвижными границами вязкого обтекания (Re<1) имеем (8.104)

В области вязкого обтекания с отрывом (1<Re<510²):

(8.105)

В области первой автомодельности (510² <Re<10⁵) соответствуют законы всплытия:

(8.106)

Для малых пузырей (капель), сохраняющих строго сферическую форму, для области Re<1 имеется теоретическое решение Адамара-Рыбчинского, учитывающее подвижность границы раздела:

(8.107)

При , т.е. при неподвижной (отвердевшей) границе раздела:

(8.108)

или (8.109)

Это известная формула Стокса для движения твердой сферы в жидкости. Общий характер зависимости показан на рис. 8.13

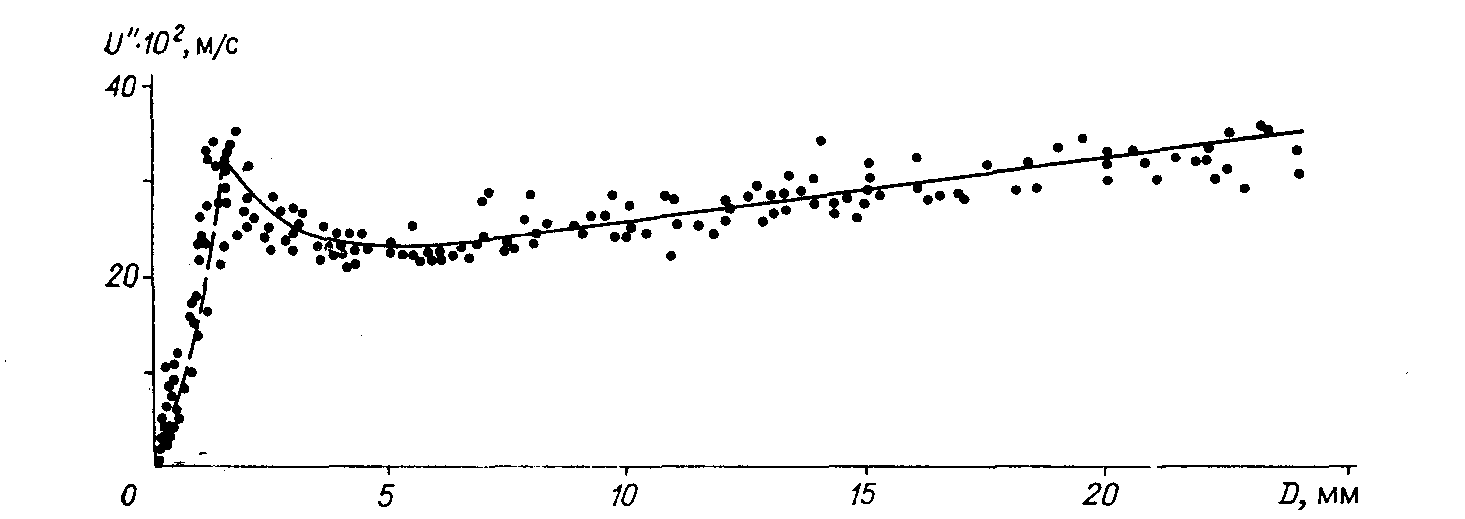
Рис. 8.13. Зависимость скорости всплытия пузырьков от их диаметра

В реальных средах реализуется закон (8.108). Это обусловлено упрочнением границы раздела диффундирующими к ней примесями, имеющимися в жидкости и газе.

При движении пузыря (капли) в канале, например круглой трубе, необходимо учитывать взаимодействие со стенками.

С этой целью, при прочих равных условиях вводится отношение эффективного радиуса пузыря к внутреннему радиусу трубы.

Общий характер зависимости при свободном всплытии пузыря показан на рис.8.13. Левая ветвь отвечает малодеформированным сферам, т.е. автомодельна относительно .

Правая ветвь, имеющая отчетливый минимум, соответствует движению деформирующихся больших пузырей и практически автомодельна относительно вязкости, т.е. критерия , т.е.:

(8.110)

Установлено, что с помощью критериев подобия опытные данные по скоростям всплытия газовых пузырьков в различных жидкостях не удается обобщить единой зависимостью. Поэтому, можно выделить пять характерных зон на зависимости скорости всплытия от радиуса (по объему) эквивалентной сферы , которые для различных жидкостей охватывают различные диапазоны и чисел Рейнольдса:

(8.111)

На рис.8.13 границы зоны отмечены для дистиллированной воды.

Зона I–сферические пузырьки при Re<1,

(8.112)

Скорость всплытия подчиняется в чистых жидкостях при условии, что , формуле:

(8.113)

Малые газовые пузырьки в воде ( >0,07 мм) всплывают, как твердые шарики, что объясняется накапливанием на поверхности раздела фаз сложных молекул поверхностно-активных веществ.

Зона II–сферические пузырьки при Re>1.

Приближенно можно принимать, что сферичность сохраняется при . При для газовых пузырьков Re = 300÷400, ≈0,6 мм, а в вязких жидкостях условие , автоматически приводит к требованию Re<1. в минеральном масле при =1,4 мм. В пределах зоны II при Re>>1 (практически при Re>40) скорость всплытия может быть рассчитана по формуле Муара:

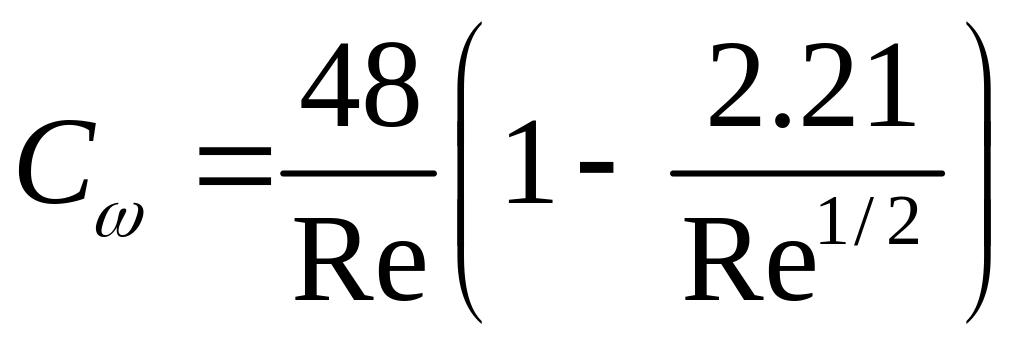(8.114)

При Рейнольдсе от 1 до 40 можно пользоваться формулой Чао:

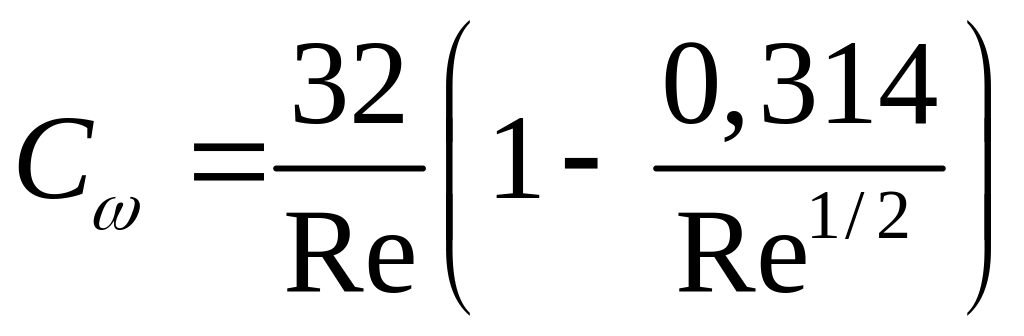(8.115)

Зона III– пузырьки, сплющенные вдоль вертикальной оси в виде сфероидов. Эта зона ограничена условием и охватывает весьма узкий диапазон размеров пузырьков (для воды =0,6÷0,8 мм, Re =400÷500). При условии Re>>1 (маловязкие жидкости – вода, этанол, криогенные жидкости и т.п.) скорость всплытия пузырьков можно рассчитывать по методике Муара.

Зона IV– пузырьки неправильной формы, всплытие которых происходит по сложной винтообразной траектории и сопровождается пульсациями формы. Для нижней границы , для верхней =0,8÷1 мм. Скорость всплытия может определяться приближенно по эмпирической формуле:

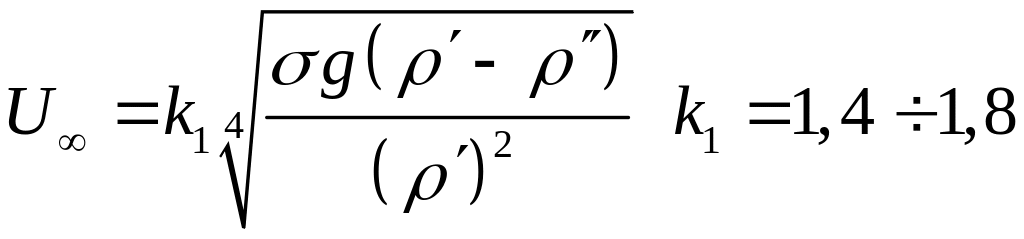(8.116)

Для воды скорость всплытия м/с.

Зона V– пузырьки объемом V>2 см³, имеющие форму практически правильного сферического сегмента. Пузырьки в жидкостях любой вязкости всплывают со скоростью:

.

При этом возможно дробление пузырьков в маловязких жидкостях.