8.7.5. Критические истечения двухфазных систем.

Для многих практических решений, в первую очередь для систем аварийной защиты АЭС, требуется рассчитывать скорость истечения двухфазного потока через отверстия или насадки.

Наиболее важной является задача об истечении насыщенной или недогретой до температуры насыщения жидкости. Истечение такой жидкости сопровождается падением давления ниже локального давления насыщения, что приводит к парообразованию внутри канала. Наличие в потоке сжимаемой фазы создает условие для появления критического режима.

Критические режимы истечения двухфазных потоков значительно отличаются от аналогичных режимов при истечении однофазной сжимаемой среды, где критический режим наступает при достижении в критическом сечении локальной скорости звука.

В двухфазном потоке достижение максимального критического расхода смеси необязательно сопряжено с установлением в критическом сечении давления, независящего от противодавления, что характерно для однофазного истечения газового потока. В критическом сечении однофазного (газового) потока устанавливается скорость звука при определенном давлении.

В двухфазном потоке само определение скорости звука не является однозначным. Причем, скорость звука зависит как от действительной структуры потока, так и от принятой физической модели процесса распространения волны возмущения.

В настоящее время не сложилась еще общепринятая точка зрения на механизм истечения и возникновения критических режимов в двухфазных потоках.

На основе обработки опытных данных по истечению насыщенной и недогретой до насыщения воды из коротких (L/D≤6) каналов небольшого диаметра (D≤9) для плотности потока может быть рекомендована следующая формула:

(8.73)

где – гидравлический коэффициент расхода, который для каналов с острой кромкой на входе равен 0,61;

и – плотность и давление заторможенного потока на уровне входного отверстия;

, здесь – давление на выходном срезе канала.

Отличие формулы (8.73) от формулы для однофазного потока состоит в том, что при определении плотности потока массы однофазной смеси используется перепад давлений , а не полная разность между давлением и противодавлением .

По мере роста недогрева и снижения давления начального давления при усилении относительной длины канала, формула (8.73) дает результат близкий к формуле для гидравлического расчета.

При давлениях > 10 Мпа критическое отношение давлений определяется по формуле:

(8.74)

если К, а при К – по формуле

(8.75)

Для коротких каналов (L/D<6) большого сечения (D>9мм) расчет по приведенным формулам дает завышенный результат.

В длинных каналах (L/D>6) при значительных недогревах ( К), расход воды можно рассчитать по формулам, аналогичным формулам для гидравлического истечения:

(8.76)

где – давление насыщения при температуре Т₀.

При критическом истечении углеводородов для длинных каналов (L/D>8) применяется критериальное уравнение:

(8.77)

где безразмерные величины , , , выражены с помощью масштабов, полученных с использованием молекулярной массы m индивидуальной газовой постоянной R, давления и температуры в критической точке р_КР, Т_КР :

(8.78)

где - скорость жидкости на входе в канал, отнесенная к полному сечению канала;

– давление на входе в канал, определяемое по формуле

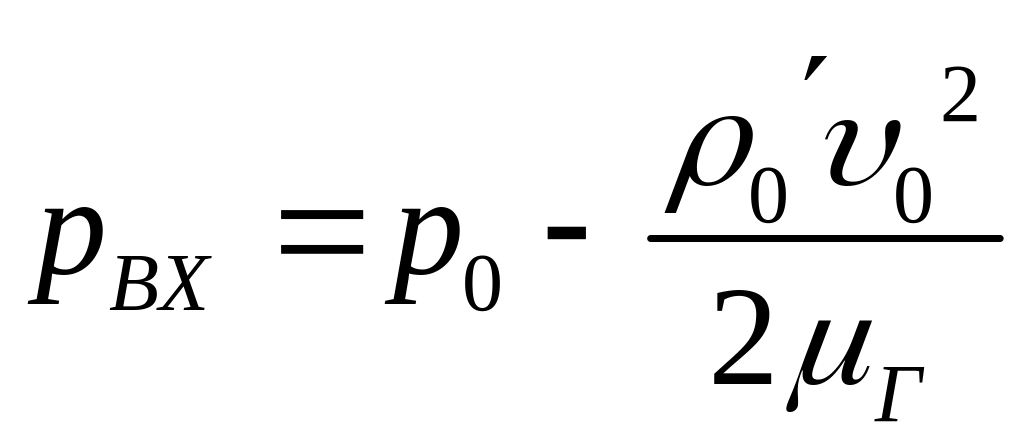(8.79)

– перегрев жидкости на входе в канал.

Безразмерные длина и диаметр канала, входящие в параметр выражаются как:

Уравнение (8.77) применимо в диапазоне π = 0,025÷0,52 (при этом может превышать 0,6); .

Порядок расчета по уравнению (8.77) следующий:

1) задаемся значением и по формуле (8.79) находим . При этом μ=0,61 для каналов с острой входной кромкой;

2) рассчитываем входной перегрев жидкости . Если получим <0, то задаемся большим значением ;

3) рассчитываем левую и правую часть уравнения (8.77) с использованием выражений (8.78). Если расхождение между ними окажется значительным, то задаемся новым значением и расчет повторяем до тех пор, пока не добьемся требуемой точности;

4) проверяем, лежат ли значения и в диапазоне применимости уравнения (8.77).