4.2. Истечение жидкости из отверстия в тонкой стенке

Рассмотрим истечение жидкости из круглого отверстия диамет­ром d₀ в вертикальной тонкой стенке сосуда (рис. 4.1).

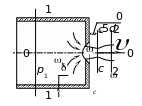
Рис. 4.1

Стенка считается тонкой, если её толщина  < 0,2d₀ и не влияет на условия истечения. Основной задачей истечения является опре­де­ление скорости истечения и расхода жидкости при следующих ус­ловиях:

1. Процесс истечения установившийся, т.е. p₁ = const.

2. Сжатие струи – полное и совершенное.

3. В сжатом сечении давление подчиняется гидростатическому за­кону распределения.

4. Скорости в верхних и нижних точках отверстия не отли­ча­ются между собой и коэффициент Кориолиса  = 1.

Для определения скорости истечения напишем уравнение Бер­нул­ли для сечений 1–1 и 2–2, учитывая, что плоскость сравнения про­ходит через центр тяжести отверстия, т.е. z₁ = z₂ = 0:

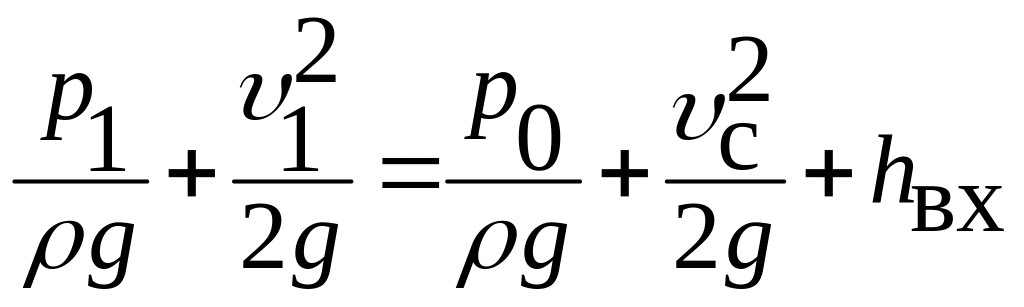. (4.2)

Анализ уравнения (4.2) показывает, что р₀ в сжатом сечении мож­но принять равным атмосферному.

Потери напора между сечениями 1–1 и 2–2 определяются по фор­му­ле Вейсбаха

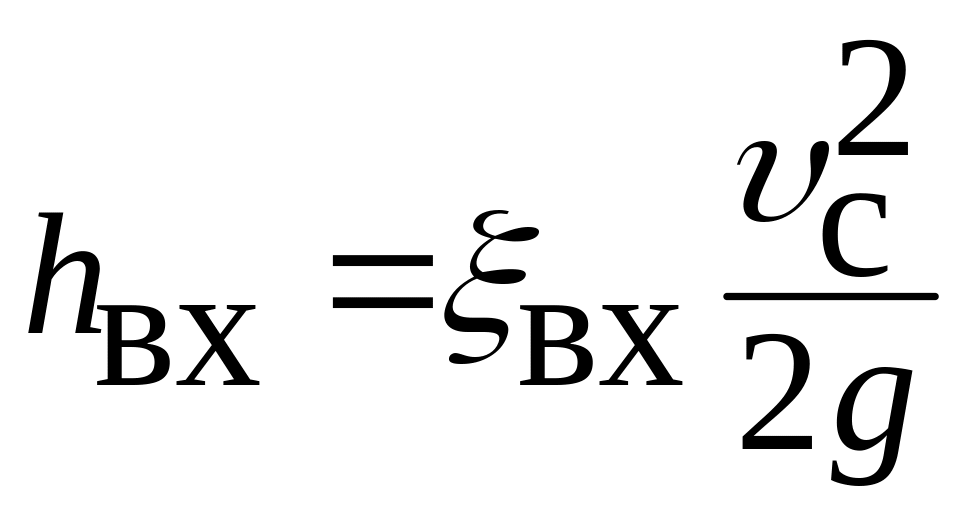, (4.3)

где вх – коэффициент сопротивления отверстия.

С учётом формулы (4.3) преобразуем уравнение (4.2) к виду:

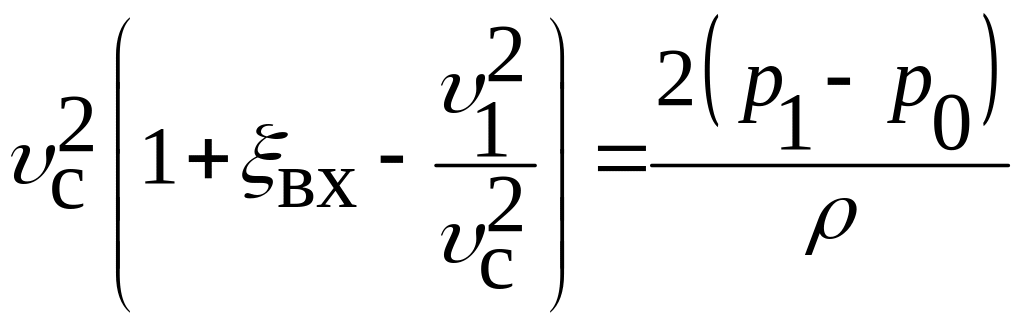. (4.4)

Решая уравнение (4.4) относительно v, находим

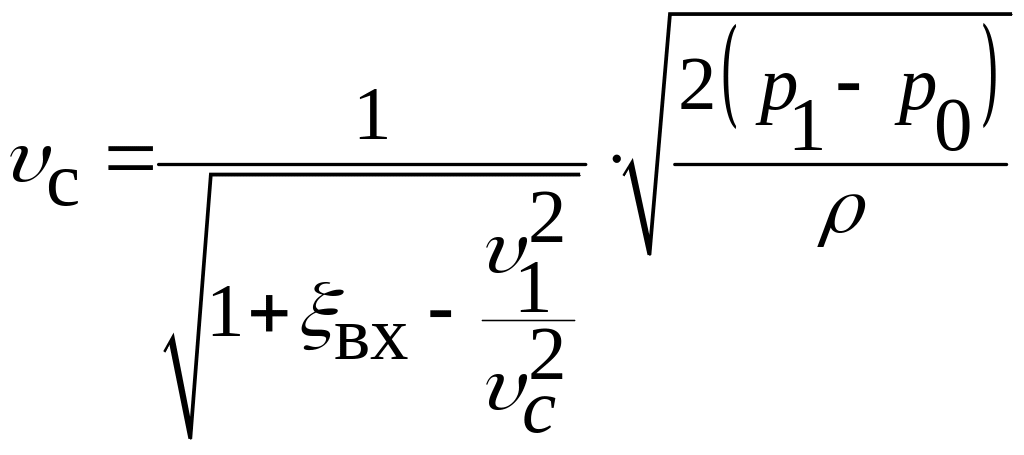. (4.5)

Преобразуем отношение , используя уравнение расхода для сечений 1–1 и с–с (см. рис. 4.1) в виде или 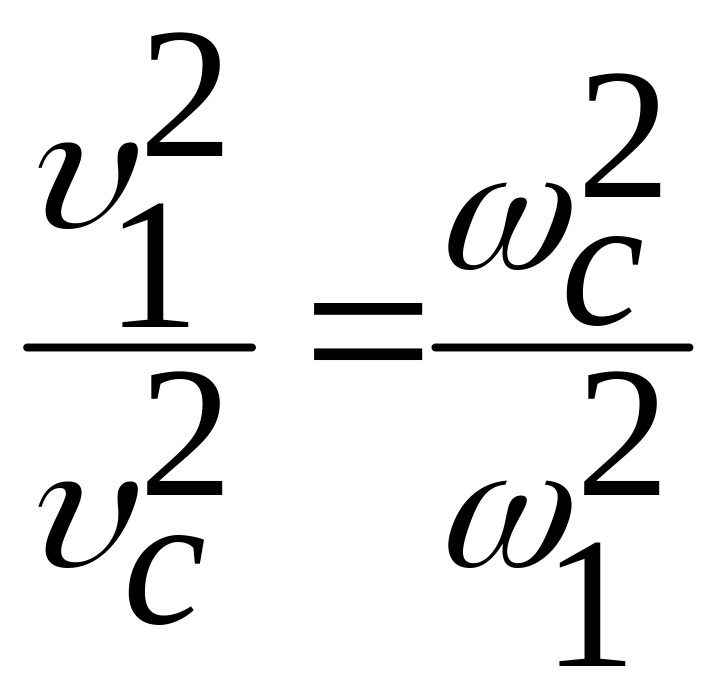. Умножив и разделив правую часть последнего равенства на , получим

.

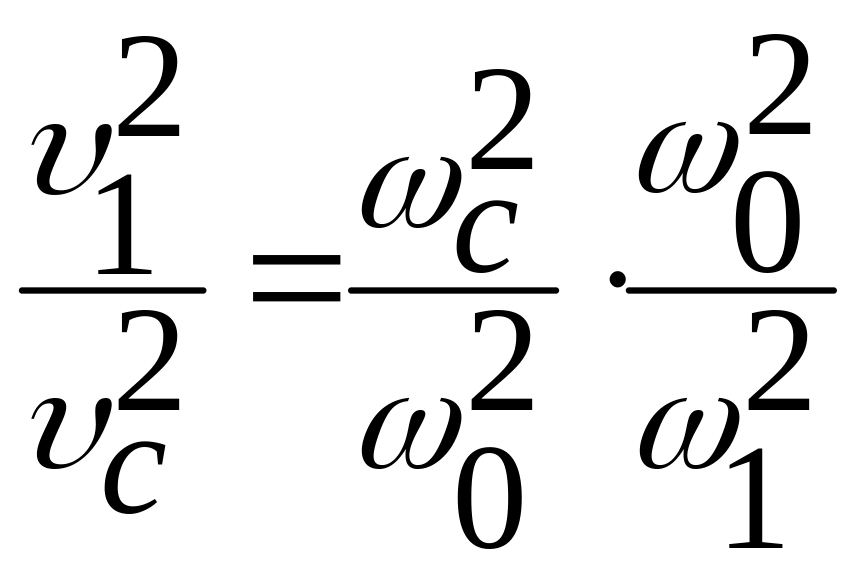Обозначив 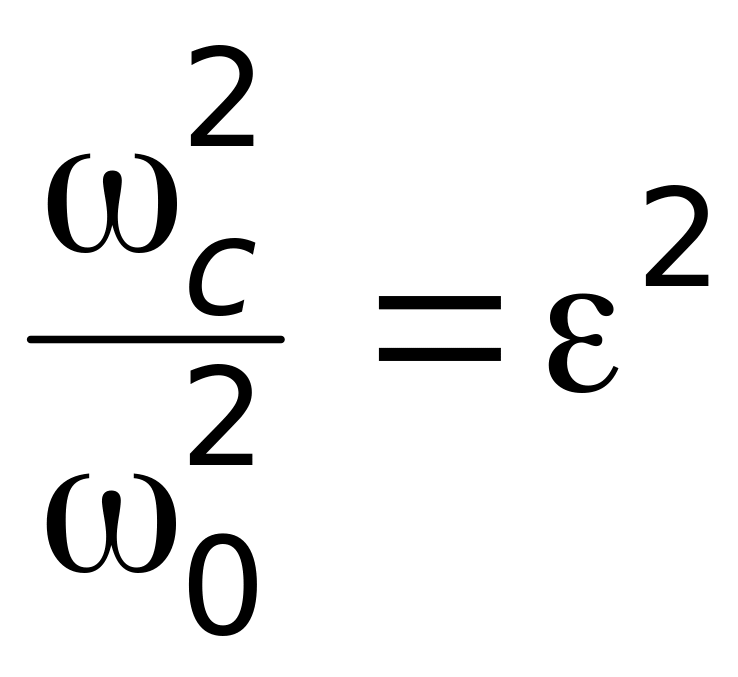и 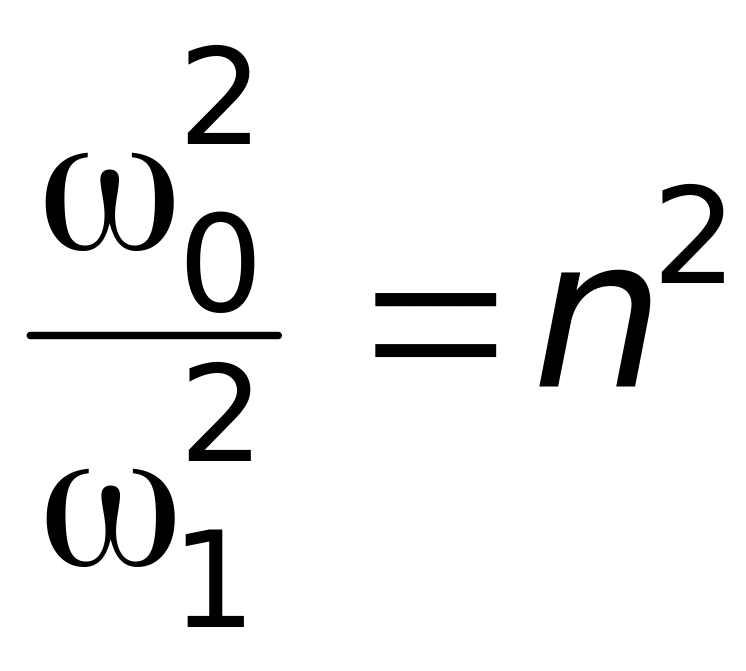, преобразуем формулу (4.5) к виду

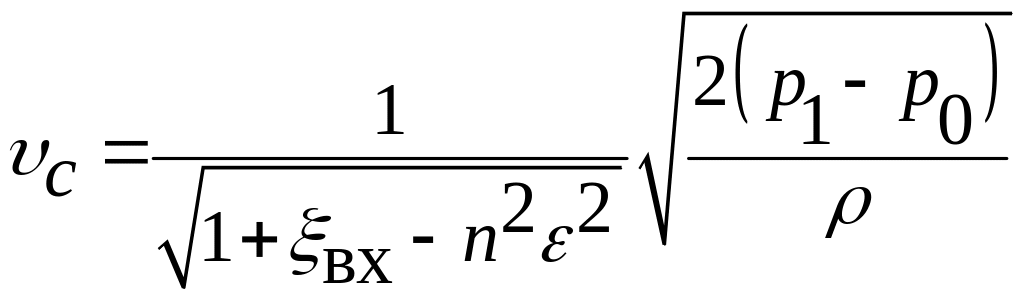. (4.6)

Введём обозначение

, (4.7)

где  – коэффициент скорости истечения, учитывающий потери скорости на местном сопротивлении (на острой кромке входного отверстия);

 = – коэффициент сжатия струи для круглых отверстий, равный 0,64;

n = – коэффициент, учитывающий влияние скорости по­тока перед входным отверстием на коэффициент скорости (при истечении из малых отверстий n  0).

С учётом обозначения (4.7), формула (4.6) принимает вид (индекс «с» опускается)

(4.8)

При истечении холодной воды через малое отверстие обычно имеем:

j » 0,97 – 0,98; x_вх » 0,06.

По коэффициенту скорости легко определить коэффициент со­про­тивления x_вх:

.

Эти коэффициенты зависят от напора Н (и, следовательно, от ско­рости истечения), вязкости жидкости, формы и размеров от­вер­стия, а поэтому и от числа Рейнольдса. Обычно принимают j = f(Re).

Траектория полёта струи при истечении жидкости при не­боль­ших скоростях и небольших высотах падения, когда можно пре­неб­речь сопротивлением окружающего струю воздуха и принять форму струи параболической, показана на рис. 4.2.

Рис. 4.2

Без большой погрешности можно считать, что частица жидкости за сжатым сечением n-n движется по инерции: по оси x – равно­мер­но, по оси z – равноускоренно, поэтому закон движения частицы жид­кости можно записать в следующем виде:

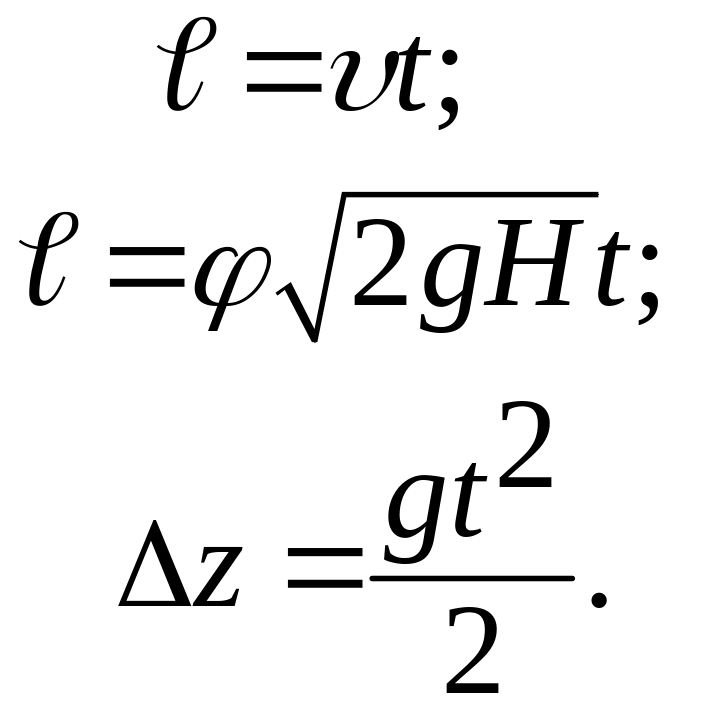(4.9)

Отсюда .

Подставляя выражение t в формулу (4.9), получим

.

Отсюда

(4.10)

Решая выражение (4.10) относительно коэффициента скорости, находим

(4.11)

Чтобы определить , надо измерить дальность полёта струи , высоту падения z и напор Н.

Расход жидкости равен произведению скорости в сжатом се­че­нии на площадь живого сечения:

.

Подставляя вместо _с и v их значения, имеем:

.

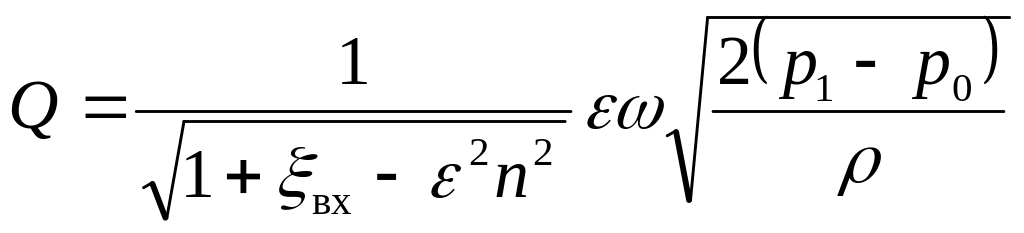Введём обозначение

, (4.12)

где  – коэффициент расхода.

С учётом обозначений в формуле (4.12) получим

_{. (4.13)}

Так как для малых отверстий коэффициент сжатия  = 0,64, а ко­эффициент скорости  = 0,97, то, в соответствии с формулой (4.12),

 =  = 0,640,97 = 0,62.

Учитывая зависимость  от , можно найти также зави­си­мость  = f(n, _вх).

При истечении из малых отверстий n  0 из формулы (4.12), находим

_{. (4.14)}

В случае истечения из сосудов со свободной поверхностью фор­мулы (4.8) и (4.13) записываются в виде:

(4.15)

(4.16)

где – высота уровня жидкости в сосуде над цент­ральным отверстием (при диаметре отверстия d << H (см. рис. 4.2).

Опытами установлено, что коэффициент  существенным обра­зом изменяется в зависимости от формы, размеров отверстия и от напора. Причём, с увеличением размеров отверстия коэффициент расхода уменьшается, а с увеличением напора уменьшается влияние размеров отверстия на коэффициент .

При неполном сжатии коэффициент расхода определяется по формулам:

– для круглых отверстий;

– для прямоугольных отверстий;

здесь 0 – коэффициент расхода для аналогичного отверстия при полном сжатии;

n – часть периметра отверстия, где отсутствует сжатие;

р – полный периметр отверстия.

Если сжатие несовершенное или неполное, то коэффициенты  и  определяются с поправками по формуле Н. Е. Жуковского:

,

где  – угол, определяемый из выражения:

;

здесь Н – глубина погружения нижней кромки отверстия;

a – высота отверстия.

При совершенном сжатии , что хорошо согласу­ется с опытными данными.

При истечении жидкости из затопленного отверстия, как пока­зали многочисленные исследования, коэффициенты , ,  будут ма­ло отличаться от коэффициентов при истечении жидкости в атмо­сферу, но в качестве напора будет действовать разность напоров Н₁–Н₂ (рис. 4.3) при р₁ = р₂.

Рис. 4.3

Расчётные формулы имеют вид:

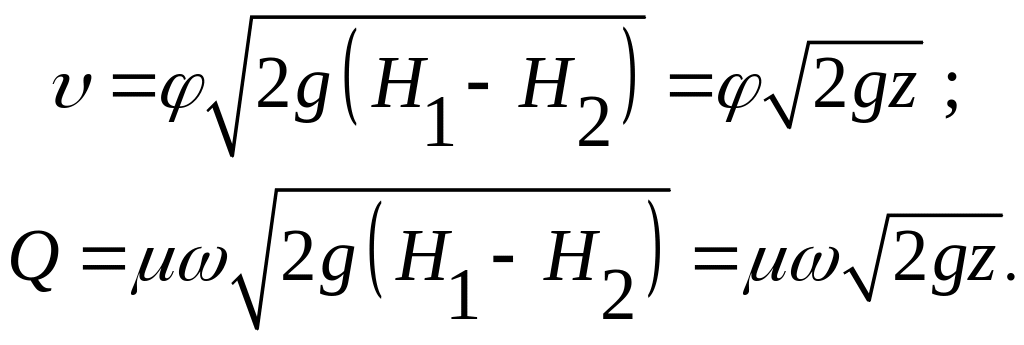_(4.17)

Если давление на свободной поверхности резервуаров не равно ат­мосферному (рис. 4.3), т.е. р₁ > p₂ > p_атм, то расчётными фор­му­ла­ми будут следующие:

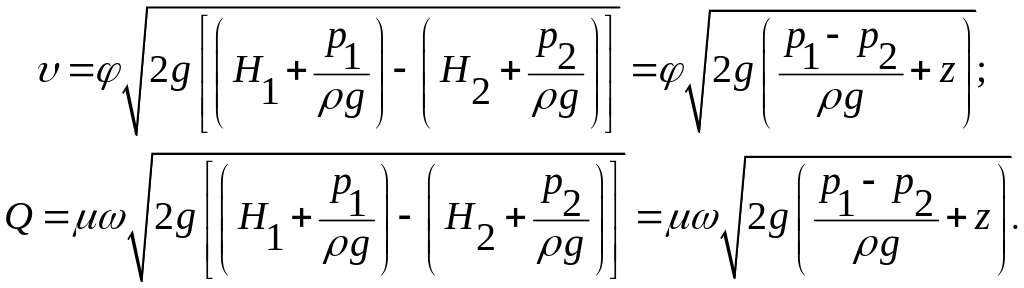(4.18)